线性代数(一)
发布时间:2023年12月18日
1.标量:标量由只有?个元素的张量表?。
x = np.array(3.0)
y = np.array(2.0)
x + y, x * y, x / y, x ** y
(array(5.), array(6.), array(1.5), array(9.))
2.向量:向量可以被视为标量值组成的列表,列向量是向量的默认?向。
x = np.arange(4)
array([0., 1., 2., 3.])
在数学中,向量x可以写为:
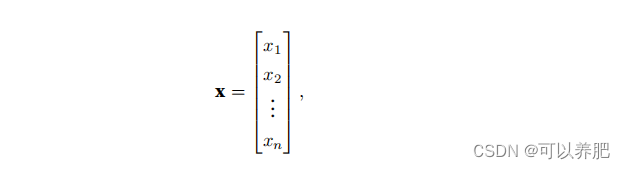
其中x1, . . . , xn是向量的元素。在代码中,我们通过张量的索引来访问任?元素。
x[3]
array(3.)
3. 矩阵:矩阵将向量从?阶推?到?阶。
A = np.arange(20).reshape(5, 4)
array([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
对于任意A ∈ R m×n,A的形状是(m,n)或m × n。

当我们交换矩阵的?和列时,结果称为矩阵的转置(transpose)。
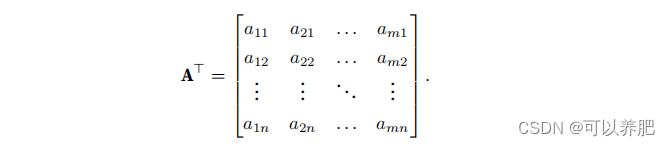
A.T
array([[ 0., 4., 8., 12., 16.],
[ 1., 5., 9., 13., 17.],
[ 2., 6., 10., 14., 18.],
[ 3., 7., 11., 15., 19.]])
4.张量:有几个中括号就是几维张量。
X = np.arange(24).reshape(2, 3, 4)
array([[[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]],
[[12., 13., 14., 15.],
[16., 17., 18., 19.],
[20., 21., 22., 23.]]])
5.范数:在线性代数中,向量范数是将向量映射到标量的函数f。
范数的的公式:

L1范数,它表?为向量元素的绝对值之和(此时P等于1):

L2范数,它表示为向量元素的平?和的平?根(此时P等于2):
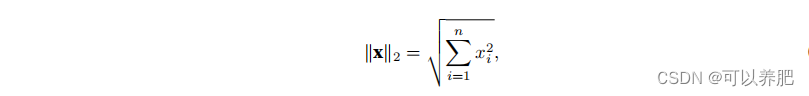
类似于向量的L2范数,矩阵X ∈ R m×n的Frobenius范数(Frobenius norm)是矩阵元素平?和的平?根:
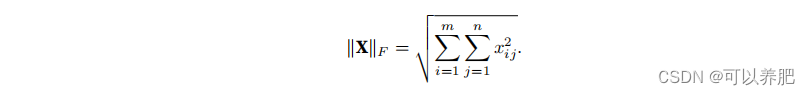
文章来源:https://blog.csdn.net/qq_39879126/article/details/135041422
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 第11章 GUI Page442~444 步骤十四:闪烁选中图元
- 计算机硬件之集成电路
- C++拾遗(三) 引用
- 记一次使用Future+ExecutorPool的多线程卡死问题
- 使用阿里云数据库,如何选择云服务器配置?
- 2023-12-29 贪心算法 分发饼干和摆动序列以及最大子数组和
- CentOS安装docker及一些命令
- 黑客必知的14个威胁建模方法
- 【MySQL】给除了主键外的字段设置自增
- playbook变量的使用