排序算法---选择排序
发布时间:2023年12月18日
1.实现流程:?
1. 把第一个没有排序过的元素设置为最小值;
2.?遍历每个没有排序过的元素;
3.?如果元素 < 现在的最小值;
4.?将此元素设置成为新的最小值;
5.?将最小值和第一个没有排序过的位置交换
选择排序执行流程
2.代码实现
let arr = [17,25,25,28,38,3,43,43,35,45,5]
function chooseSort() {
let indexMin = 0;
// 选择n-1次
for (let i=0; i<arr.length-1; i++) {
let indexMin = i;
for (let j=i+1; j<arr.length; j++) {
if (arr[j]<arr[indexMin]) {
indexMin = j;
}
}
if (indexMin != i) {
let temp = arr[i];
arr[i] = arr[indexMin];
arr[indexMin] = temp;
}
}
console.log(arr)
}
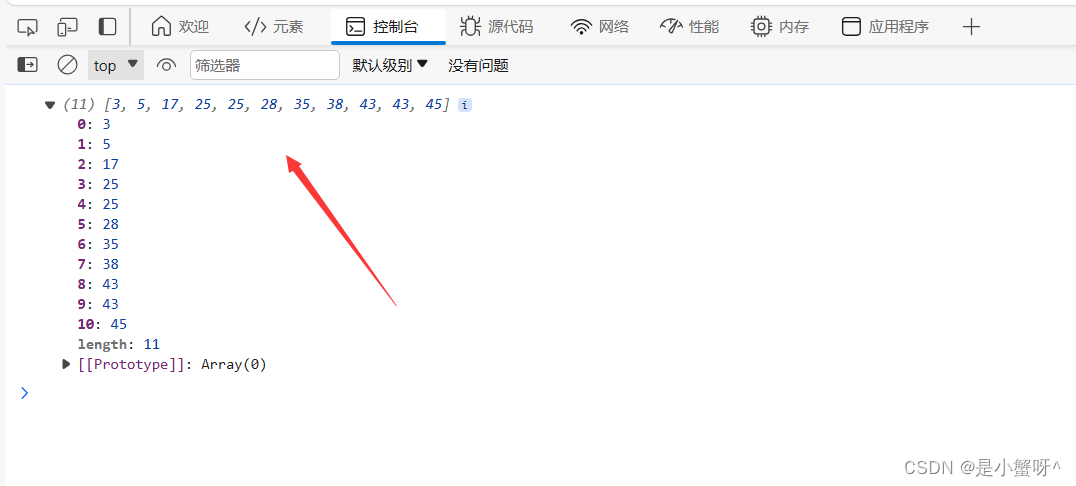
chooseSort()运行结果:
3.复杂度分析
1. 时间复杂度:找出执行次数最多的语句即可
if (arr[j]<arr[indexMin]) {
indexMin = j;
}基于上述每一趟比较的次数,可以得到总的比较次数,就是这个判断语句执行的次数
=> 当i=0时, 需要比较n-1-0次
? ? ?当i=1时,需要比较n-1-1次
? ? ?......
? ? ?当i=n-3时, 需要比较n-1-(n-3) = 2
? ? ?当i=n-2时, 需要比较n-1-(n-2) = 1
? ? ?当i=n-1时, 需要比较n-1-(n-1) = 0
=> ?(n-1)+(n-2)+(n-3)+...+1+0 = [n(n-1)]/2 ?= n^2/2 - n/2 + 1/2
=> 去掉系数、低阶和常量 ?
=> 则时间复杂度为 ?O(n^2)
2. 空间复杂度: 选择排序中并没有用到额外的空间,所以空间复杂度为 O(1)
3. 选择排序是不稳定的排序算法:从上述的视频可以看出,数组中有两个43,然而在排完序后,原本前面的43跑到了后面
文章来源:https://blog.csdn.net/m0_61495539/article/details/134911070
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 信息安全领域的行业新宠——CISP-DSG
- 【ARM Cortex-M 系列 1.1 -- Cortex-M33 与 M4 差异 详细介绍】
- Java 6种常见拷贝集合方式深浅拷贝测试
- 完成实验十的ko-ngxugan
- 回溯算法详解
- Flutter使用stack来实现悬浮UI
- GB 4806.5-2016 食品接触玻璃制品 餐具检测 第三方检测机构 实验室
- openmediavault(OMV) (24)在线网盘(2)kodcloud
- 航芯ACM32G103开发板评测 02-GPIO输入输出
- 街头霸王II神经网络AI训练项目