算法训练营Day17

#Java #二叉树 #dfs

开源学习资料

Feeling and experiences：

找树左下角的值：力扣题目链接

给定一个二叉树的 根节点 root，请找出该二叉树的?最底层?最左边?节点的值。

假设二叉树中至少有一个节点。

找到题目的关键词：最底层，最左边

提到了层数，显然是要去找最大深度的。

思路：利用深度优先搜索，定义全局变量，把得到的结果赋值给全局变量，走不通了，那最后赋值给全局变量的则是最后的结果；

代码如下：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //设置全局变量 
    int maxDeep = -1;
    int mostLeftnode = 0;
    public int findBottomLeftValue(TreeNode root) {
    //dfs
    dfs(root,0);
    return mostLeftnode;
    }
    public void dfs(TreeNode node , int depth){
        if(node == null){
            return;
        }
        if(depth > maxDeep){
            maxDeep = depth;
            mostLeftnode = node.val;
        }
        dfs(node.left,depth+1);
        dfs(node.right,depth+1);
    }
}

在这里，我设置了两个全局变量，一个最大深度，一个最大左值。?

通过递归深度比较，会把最深的左子节点的值赋值给全局变量的最大左值。

层序遍历的写法：

class Solution {
    public int findBottomLeftValue(TreeNode root) {
        int ret = 0;
        Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode p = queue.poll();
            if (p.right != null) {
                queue.offer(p.right);
            }
            if (p.left != null) {
                queue.offer(p.left);
            }
            ret = p.val;
        }
        return ret;
    }
}

?

路径总和：力扣题目链接

给你二叉树的根节点?root 和一个表示目标和的整数?targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和?targetSum 。如果存在，返回 true ；否则，返回 false 。

这道题和之前用dfs写的题大同小异：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
   
    public boolean hasPathSum(TreeNode root, int targetSum) {
    //是否能找到一条路径，使得其路径上的值等于target
    return dfs(root , targetSum,0);
    }
    public boolean dfs(TreeNode node,int targetSum,int currentSum){
        if(node == null){
            return false;
        }
        currentSum += node.val;
        //检查是否到达叶子节点，并且路径和是否等于目标和
        if(node.left == null && node.right == null){
            return currentSum == targetSum;
        }
       
       return dfs(node.left,targetSum,currentSum) || dfs(node.right,targetSum,currentSum);

    }
}

从中序与后序遍历序列构造二叉树：力扣题目链接

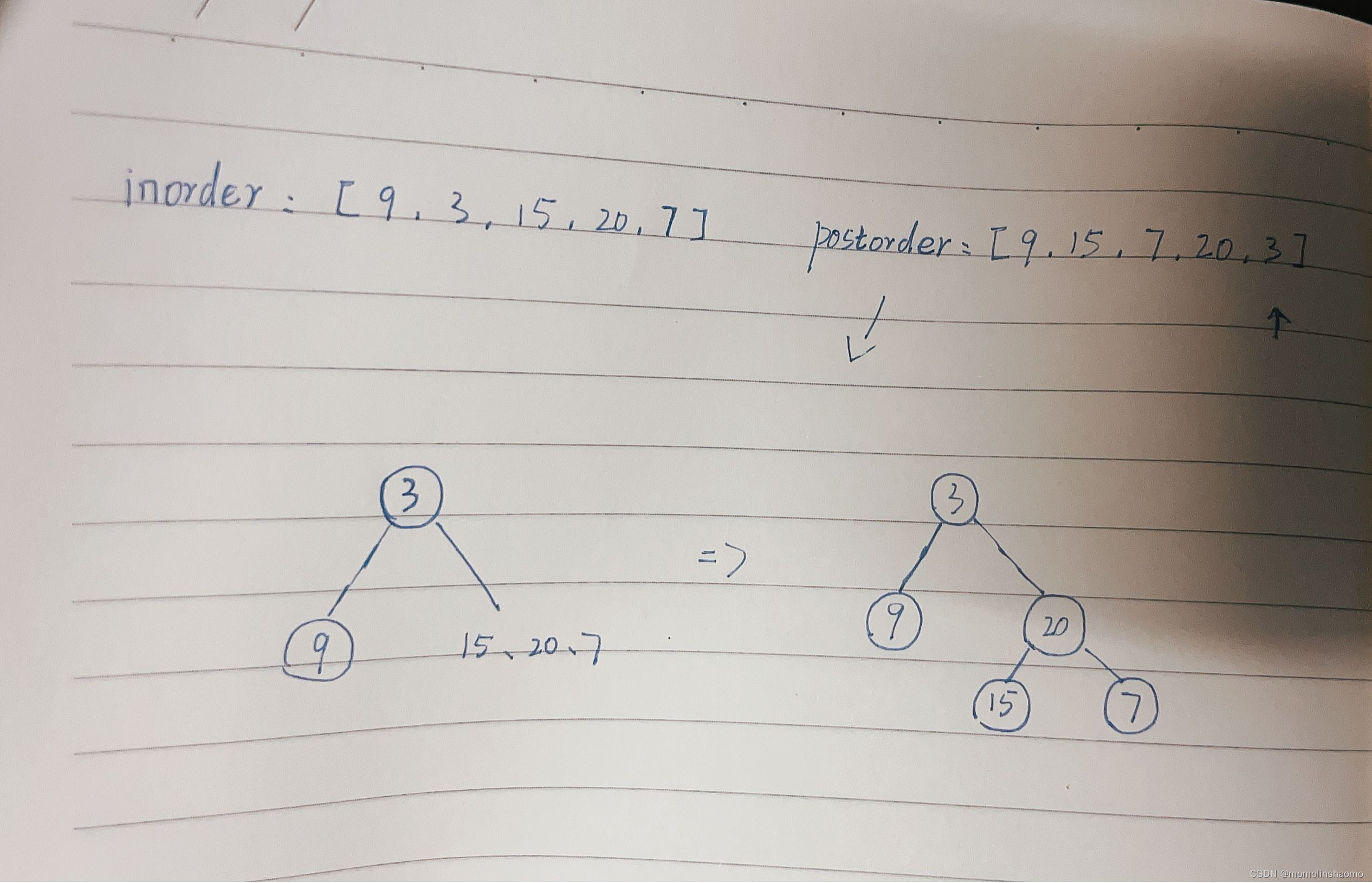
给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗?二叉树?。

在数据结构中，我们知道中序遍历和后序遍历可以唯一确定一棵二叉树。

思路：从后序遍历结果来看，最后一个即为根节点root，找到根节点在中序遍历结果中的位置，就能直到它的左右节点有哪些。

利用递归，来求解。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    Map<Integer, Integer> map;  // 方便根据数值查找位置
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        map = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) { // 用map保存中序序列的数值对应位置
            map.put(inorder[i], i);
        }

        return findNode(inorder,  0, inorder.length, postorder,0, postorder.length);  // 前闭后开
    }

    public TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {
        // 参数里的范围都是前闭后开
        if (inBegin >= inEnd || postBegin >= postEnd) {  // 不满足左闭右开，说明没有元素，返回空树
            return null;
        }
        int rootIndex = map.get(postorder[postEnd - 1]);  // 找到后序遍历的最后一个元素在中序遍历中的位置
        TreeNode root = new TreeNode(inorder[rootIndex]);  // 构造结点
        int lenOfLeft = rootIndex - inBegin;  // 保存中序左子树个数，用来确定后序数列的个数
        root.left = findNode(inorder, inBegin, rootIndex,
                            postorder, postBegin, postBegin + lenOfLeft);
        root.right = findNode(inorder, rootIndex + 1, inEnd,
                            postorder, postBegin + lenOfLeft, postEnd - 1);

        return root;
    }
}

图例如下：

?

Fighting!

?

?

?

?

?