算法设计：欧几里德算法求最大公约数问题

题目：欧几里德算法

计算两个正整数m,n的最大公约数

1. 欧几里德算法：gcd(m,n)

其中m>=n,其递归定义为：

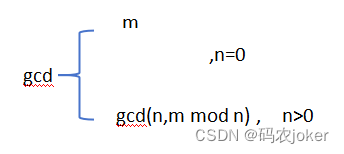
算法思路：

第一步：如果n=0，返回m的值作为结果，同时过程结束。否则就进入第二步。

第二步：m mod n，将余数赋值给r。

第三部：将n的值赋值给m,将r的值赋值n返回第一步。

例如：Gcd(60,24)

此时m=60,n=24;由于n不等于0，60/24=2……12。将n的值赋值给m,将r的值赋值给n，(m=24,n=12)

Gcd(24,12);m=24,n=12;由于n不等于0，24/12=2。最大公约数为12。

代码：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
void Compare(int m, int n) {
	if (m < n) {
		m = n;
		n = m;
	}
}
int Gcd(int m,int n) {
	int r;//定义余数
	Compare(m,n);
	do {
		r = m % n;
		m = n;
		n = r;
	}
	while (n != 0);
		return m;//当n=0时，返回m的值

}
int main() {
	int m, n;
	printf("请输入两个正整数：");
	scanf_s("%d%d", &m,&n);
	Gcd(m,n);
	printf("最大公约数为：%d", Gcd(m, n));
}

运行截图：

总结归纳：

求m,n的最大公约数为问题，转化为求n和m除以n的余数的最大公约数问题，把问题转化，是递归定义的。