算法设计与分析-图算法小结BFS/DFS/Topologic/Dijkstra/Floyd/最大流

图

注:CSDN貌似不支持较长公式，可以复制到Markdown编辑器查看

图的表示

1. 邻接矩阵 空间复杂度 $\Theta (V^2)$
2. 邻接链表 空间复杂度 $\Theta (V+E)$

BFS

• 邻接链表 时间复杂度 $\Theta (V+E)$

• 
  void BFS(Graph G, int v) {//从顶点v出发，广度优先遍历图G
      visit(v);//访问初始顶点
      vsited[v] = true;//标记访问
      Enqueue(Q, v);//入队
      while (!isEmpty(Q)) {
          DeQueue(Q, v);//出队
          for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w))
              if (!visited[w]) {//w为v未访问邻接顶点
                  visit(w);//访问
                  visited[w] = true;//标记
                  EnQueue(Q, w);//进队
              }
      }
  }
  

• 无权最短路径问题

• 前驱子图，BFS生成树

DFS

• 递归是核心

• void DFS(Graph G,int v){
      visit(v);
      visited[v]=true;
      for(w=FirstNeighbour(G,v);w>=0;w=NextNeighor(G,v,w)){
          if(!visited[w]){
              DFS(G,w);
          }
      }
  }
  

Topolpgical sort

• 拓扑排序是可以用来简单地判环的,若能则无环。

• // deg是入度，在存图的时候需要录入数据
  // A是排序后的数组
  int deg[MAXN], A[MAXN];
  bool toposort(int n)
  {
      int cnt = 0;
      queue<int> q;//若是priority_queue,则可以输出字典序最大/小拓扑序
      for (int i = 1; i <= n; ++i)
          if (deg[i] == 0)
              q.push(i);
      while (!q.empty())
      {
          int t = q.front();
          q.pop();
          A[cnt++] = t;
          for (auto to : edges[t])
          {
              deg[to]--;
              if (deg[to] == 0) // 出现了新的入度为0的点
                  q.push(to);
          }
      }
      return cnt == n;//
  }
  

最小生成树

• [Kruskal][https://blog.csdn.net/yf_li123/article/details/75195549] , [Prim算法][https://blog.csdn.net/yf_li123/article/details/75148998]

单源最短路径

1. Bellman-Ford

//检测有无负环
//spfa可以计算有负环 单元最短路径
void bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);

    dist[1] = 0;
    for (int i = 0; i < k; i ++ )
    {
        memcpy(last, dist, sizeof dist);
        for (int j = 0; j < m; j ++ )
        {
            auto e = edges[j];
            dist[e.b] = min(dist[e.b], last[e.a] + e.c);
        }
    }
}

2. [Topological-sort][https://blog.csdn.net/dragon8462_/article/details/119746134]

//只能有向无环图

3. Dijisktra

   [Dijkstra算法介绍及其优先队列优化和斐波那契堆优化][https://blog.csdn.net/qq_33903332/article/details/116095232]

//
int dijkstra()
{
    // 初始化， 一号点到起点的距离为0， 其他点到起点的距离为正无穷
    memset(dist, 0x3f, sizeof dist); 
    dist[1] = 0;
    for(int i = 0; i < n -1; i ++) // n - 1迭代
    {
        int t = -1;
            // 找到未加到 st 集合的最短距离
            for(int j = 1; j <= n ; j ++)
                if( !st[j] && (t == -1 || dist[t] > dist[j]) )
                    t = j;
            // 将t点加入到集合
                    st[t] = true;
             // 更新从t出去的所有的边，他组成的路径能不能更强其他点的距离
                    for(int j = 1; j <= n; j++)
                    dist[j] = min(dist[j], dist[t] + w[t][j]); 
    }
}

//堆优化
const int N = 1e5+7;
const int INF = 0x3f3f3f3f;
struct Node{
	int to, w;
};//to指向另一端的结点, w表示边的长度 
vector<Node> g[N];//邻接表存储图 
int n, m, s;//n-结点数, m-边数, s-源点 
int d[N];//记录源点s到图中所有结点的最短路 
bool vis[N];//在Dijkstra算法中用于记录结点是否访问 
void Dijkstra_2(int s) {
	memset(d, 0x3f, sizeof(d));//初始距离设为INF 
	d[s] = 0;//源点到源点的距离为 0
	//使用优先队列实现堆, 默认以pair的first从大到小排序
	priority_queue< pair<int, int> > q;
	q.push(make_pair(0, s));//源点放入堆中 
	while (!q.empty()) {
		pair<int, int> t = q.top(); q.pop();
		int from = t.second;
		if (vis[from]) continue;//跳过已经访问过的结点 
		vis[from] = true;
		//以该点为中间结点更新最短路径 
		for (int i = 0; i < g[from].size(); i++) {
			int to = g[from][i].to;
			int w = g[from][i].w;
			if (d[to] > d[from] + w) {
				d[to] = d[from] + w;
				if (vis[to] == false) {
					//first以负数存储, d小的反而大, 在堆顶 
					q.push(make_pair(-d[to], to));
				}
			}
		}
	}
}

所有点对最短路径

1. Dijisktra跑n遍(不带负权)-Greedy

2. Floyd-Warshall-DP (假设权重可以为负，但不能有权重为负的环路。)

   $d_{ij}^k$为从结点 $i $到 $j$ 的所有中间结点全部取自集合 { 1 , 2 , . . . , k } \{1,2,...,k\} {1,2,...,k}的一条最短路径的权重。

   当$k=0$时，也就是从结点 $i $到 $j$ 的路径上不包括任何结点。这样路径上只有$(i,j)$这一条边，此时$d_{ij}^0=w(i,j)$。

   当$k?1$时，又可以分为两种情况：

   1. 结点 $i $到 $j$ 的最短路径 $p$，没有经过结点 $k$，此时 $d_{ij}^k=d_{ij}^{k?1}$。
   2. 结点 $i $到 $j$ 的最短路径 $p$，经过结点了 $k$，$d_{ij}^k=d_{ik}^{k?1}+d_{kj}^{k?1}$。

   D

   $d_{ij}^k= \begin{cases} w(i,j)& k=0\ min{d_{ij}^{k-1}, d_{ik}^{k-1} + d_{kj}^{k-1} } & k\geqslant 1\ \end{cases}\$

   PI(前驱矩阵)

   $\pi_{ij}^k= \begin{cases} \pi_{ij}^{k-1} & d_{ij}^{k-1} \leqslant d_{ik}^{k-1} + d_{kj}^{k-1}\ \pi_{kj}^{k-1} & d_{ij}^{k-1} \gt d_{ik}^{k-1} + d_{kj}^{k-1}\ \end{cases}\$

   FLOYD-WARSHALL(W)
     n = W.rows
     D0 = W
     let P = n x n martix initialized with nil//前驱矩阵
     for i = 1 to n
       for j = 1 to n
         if i != j and D[i, j] < ∞
           P[i, j] = i
     for k = 1 to n
         Dk = new n x n matrix //可以直接用两个矩阵颠倒
       for i=1 to n
           for j= 1 to n
         		D[ij] = min(Dk-1[ij], Dk-1[ik] + Dk-1[kj])
   

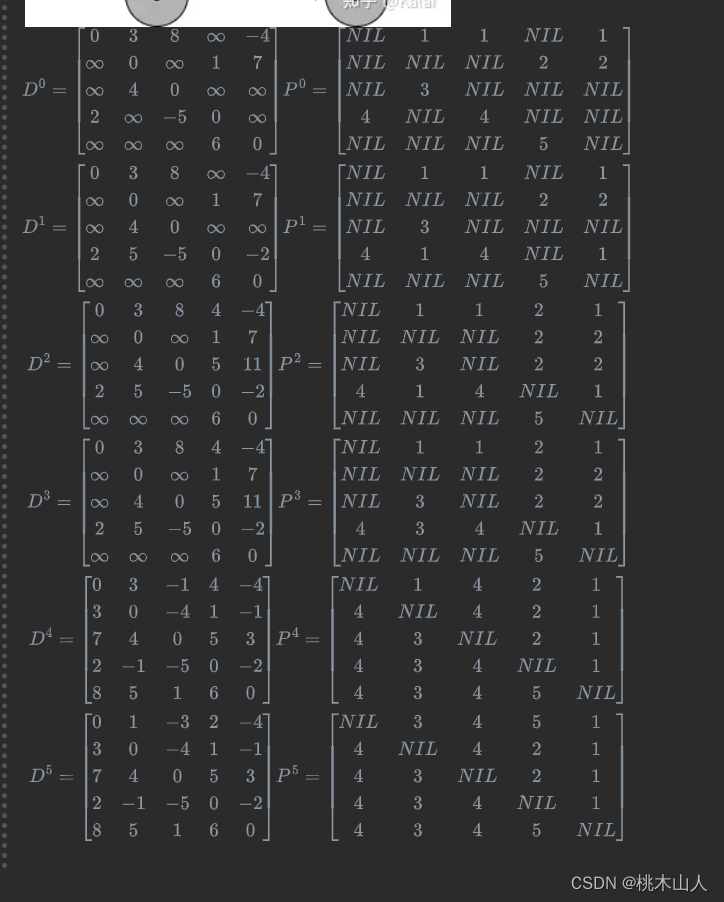
$$D^0 = \begin{bmatrix} 0 & 3 & 8 & \infty & -4 \ \infty & 0 & \infty & 1 & 7 \ \infty & 4 & 0 & \infty & \infty \ 2 & \infty & -5 & 0 & \infty \ \infty & \infty & \infty & 6 & 0 \ \end{bmatrix} P^0 = \begin{bmatrix} NIL & 1 & 1 & NIL & 1 \ NIL & NIL & NIL & 2 & 2 \ NIL & 3 & NIL & NIL & NIL \ 4 & NIL & 4 & NIL & NIL \ NIL & NIL & NIL & 5 & NIL \ \end{bmatrix}\ D^1 = \begin{bmatrix} 0 & 3 & 8 & \infty & -4 \ \infty & 0 & \infty & 1 & 7 \ \infty & 4 & 0 & \infty & \infty \ 2 & 5 & -5 & 0 & -2 \ \infty & \infty & \infty & 6 & 0 \ \end{bmatrix} P^1 = \begin{bmatrix} NIL & 1 & 1 & NIL & 1 \ NIL & NIL & NIL & 2 & 2 \ NIL & 3 & NIL & NIL & NIL \ 4 & 1 & 4 & NIL & 1 \ NIL & NIL & NIL & 5 & NIL \ \end{bmatrix}\ D^2 = \begin{bmatrix} 0 & 3 & 8 & 4 & -4 \ \infty & 0 & \infty & 1 & 7 \ \infty & 4 & 0 & 5 & 11 \ 2 & 5 & -5 & 0 & -2 \ \infty & \infty & \infty & 6 & 0 \ \end{bmatrix} P^2 = \begin{bmatrix} NIL & 1 & 1 & 2 & 1 \ NIL & NIL & NIL & 2 & 2 \ NIL & 3 & NIL & 2 & 2 \ 4 & 1 & 4 & NIL & 1 \ NIL & NIL & NIL & 5 & NIL \ \end{bmatrix}\ D^3 = \begin{bmatrix} 0 & 3 & 8 & 4 & -4 \ \infty & 0 & \infty & 1 & 7 \ \infty & 4 & 0 & 5 & 11 \ 2 & 5 & -5 & 0 & -2 \ \infty & \infty & \infty & 6 & 0 \ \end{bmatrix} P^3 = \begin{bmatrix} NIL & 1 & 1 & 2 & 1 \ NIL & NIL & NIL & 2 & 2 \ NIL & 3 & NIL & 2 & 2 \ 4 & 3 & 4 & NIL & 1 \ NIL & NIL & NIL & 5 & NIL \ \end{bmatrix}\ D^4 = \begin{bmatrix} 0 & 3 & -1 & 4 & -4 \ 3 & 0 & -4 & 1 & -1 \ 7 & 4 & 0 & 5 & 3 \ 2 & -1 & -5 & 0 & -2 \ 8 & 5 & 1 & 6 & 0 \ \end{bmatrix} P^4 = \begin{bmatrix} NIL & 1 & 4 & 2 & 1 \ 4 & NIL & 4 & 2 & 1 \ 4 & 3 & NIL & 2 & 1 \ 4 & 3 & 4 & NIL & 1 \ 4 & 3 & 4 & 5 & NIL \ \end{bmatrix}\ D^5 = \begin{bmatrix} 0 & 1 & -3 & 2 & -4 \ 3 & 0 & -4 & 1 & -1 \ 7 & 4 & 0 & 5 & 3 \ 2 & -1 & -5 & 0 & -2 \ 8 & 5 & 1 & 6 & 0 \ \end{bmatrix} P^5 = \begin{bmatrix} NIL & 3 & 4 & 5 & 1 \ 4 & NIL & 4 & 2 & 1 \ 4 & 3 & NIL & 2 & 1 \ 4 & 3 & 4 & NIL & 1 \ 4 & 3 & 4 & 5 & NIL \ \end{bmatrix}\\$$

csdn好像不支持这么长的公式
可以参考算法导论或者下面的图片

最大流（流网络的最大容量问题，最小分割问题

参考：https://zhuanlan.zhihu.com/p/356840694
#include <queue>
#include <stdio.h>
#include <cstring>
#define INF  2147483467
using namespace std;
using ll = long long;

const int maxn = 520010, maxm = 520010; 
int n, m, s, t;

struct Edge{
    ll to, next, weight;
};
Edge edges[maxm]; 
int edge_cnt = 1, head[maxn], cur[maxn];

void add(int x,int y,int w){
    edges[++edge_cnt].next = head[x];
    edges[edge_cnt].to = y;
    edges[edge_cnt].weight = w;
    head[x] = edge_cnt;
}

int level[maxn];
bool bfs(){
    memset(level, 0, sizeof(level));
    memcpy(cur, head, sizeof(head));
    queue<int> q;
    q.push(s);
    level[s] = 1;
    while (!q.empty()){
        int u = q.front();
        q.pop();
        for (int i = head[u]; i != 0; i = edges[i].next){
            ll v = edges[i].to, flow = edges[i].weight;
            if (flow > 0 && level[v] == 0){
                level[v] = level[u] + 1;
                q.push(v);
            }
        }   
    }
    return (level[t] != 0);
}

int dfs(int p = s, int cur_flow = INF){
    if (p == t) return cur_flow;
    ll ret = 0;
    for (int i = cur[p]; i != 0; i = edges[i].next){
        cur[p] = i;
        ll v = edges[i].to, vol = edges[i].weight;
        if (level[v] == level[p] + 1 && vol > 0){
            int f = dfs(v, min(cur_flow - ret, vol));
            edges[i].weight -= f;
            edges[i^1].weight += f;
            ret += f;
            if (ret == cur_flow) return ret;
        }
    }
    return ret;
}

ll dinic(){
    ll max_flow = 0;
    while (bfs()){
        max_flow += dfs();
    }
    return max_flow;
}

int main(){
    scanf("%d %d %d %d", &n, &m, &s, &t);
    for (int i = 1; i <= m ; ++i){
        int x, y, w;
        scanf("%d %d %d", &x, &y, &w);
        add(x, y, w);
        add(y, x, 0);
    }
    printf("%lld", dinic());
    return 0;
}