光栅化渲染：投影算法

在上一章中，我们对光栅化渲染技术进行了高级概述。 它可以分解为两个主要阶段：首先，将三角形的顶点投影到画布上，然后对三角形本身进行光栅化。 在这种情况下，光栅化意味着将三角形的形状“分解”为像素或光栅元素正方形； 这就是过去所说的像素。

在本章中，我们将回顾第一步。 这个方法我们在前两课已经介绍过了，这里就不再解释了。 如果你对透视投影背后的原理有任何疑问，请再次查看这些课程。 然而，在本章中，我们将研究一些与投影相关的新技巧，当我们学习透视投影矩阵的课程时，这些技巧将很有用。 我们将学习一种将投影顶点坐标从屏幕空间重新映射到 NDC 空间的新方法。 我们还将详细了解 z 坐标在光栅化算法中的作用以及在投影阶段应如何处理它。

请记住，正如上一章已经提到的，光栅化渲染技术的目标是解决可见性或隐藏表面问题，即确定 3D 对象的哪些部分是可见的，哪些部分是隐藏的。

NSDT工具推荐：?Three.js AI纹理开发包?-?YOLO合成数据生成器?-?GLTF/GLB在线编辑?-?3D模型格式在线转换?-?可编程3D场景编辑器?-?REVIT导出3D模型插件?-?3D模型语义搜索引擎

1、投影：我们要解决什么问题？

在光栅化算法的那个阶段我们要解决什么问题？ 正如上一章所解释的，光栅化的原理是查找图像中的像素是否与三角形重叠。 为此，我们首先需要将三角形投影到画布上，然后将它们的坐标从屏幕空间转换为光栅空间。 然后，像素和三角形被定义在同一空间中，这意味着可以比较它们各自的坐标（我们可以根据三角形顶点的光栅空间坐标检查给定像素的坐标）。

因此，该阶段的目标是将构成三角形的顶点从相机空间（camera space）转换为光栅空间（raster space）。

2、投影顶点：注意 Z 坐标！

在前两课中，我们提到当我们计算 3D 点的栅格坐标时，我们最终需要的是它的 x 和 y 坐标（3D 点在图像中的位置）。 快速提醒一下，请记住，这些 2D 坐标是通过将相机空间中 3D 点的 x 和 y 坐标除以该点各自的 z 坐标（我们称为透视除法），然后重新映射生成的 2D 坐标来获得的 从屏幕空间到 NDC 空间，然后从 NDC 空间到光栅空间。 请记住，由于图像平面位于近裁剪平面，因此我们还需要将 x 坐标和 y 坐标乘以近裁剪平面。 同样，我们在前两课中非常详细地解释了这个过程：

请注意，到目前为止，我们一直将屏幕空间中的点视为本质上的 2D 点（我们不需要在透视划分后使用点的 z 坐标）。 但从现在开始，我们将屏幕空间中的点声明为 3D 点，并将它们的 z 坐标设置为相机空间点的 z 坐标，如下所示：

此时最好将投影点 z 坐标设置为原始点 z 坐标的倒数，正如你现在所知，原始点 z 坐标为负值。 处理正 z 坐标将使以后的一切变得更简单（但这不是强制性的）：

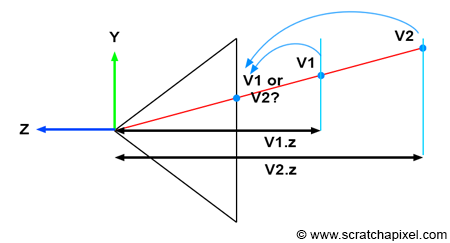
图 1：当相机空间中的两个顶点具有相同的 2D 光栅坐标时，我们可以使用原始顶点的 z 坐标来找出哪个顶点在另一个顶点的前面（从而确定哪个顶点可见）

需要跟踪相机空间中的顶点 z 坐标来解决可见性问题。 如果查看图 1，就会更容易理解其中的原因。想象一下两个顶点 v1 和 v2，当投影到画布上时，它们具有相同的光栅坐标（如图 1 所示）。 如果我们将 v1 投影在 v2 之前，那么 v2 在应该是 v1 的情况下将在图像中可见（v1 明显在 v2 前面）。 但是，如果我们将顶点的 z 坐标与其 2D 光栅坐标一起存储，则可以使用这些坐标来定义最接近相机的点，而与顶点投影的顺序无关（如代码片段所示）：

// project v2
Vec3f v2screen;
v2screen.x = near * v2camera.x / -v2camera.z;
v2screen.y = near * v2camera.y / -v2camera.z;
v2screen.z = -v2cam.z;

Vec3f v1screen;
v1screen.x = near * v1camera.x / -v1camera.z;
v1screen.y = near * v1camera.y / -v1camera.z;
v1screen.z = -v1camera.z;

// If the two vertices have the same coordinates in the image then compare their z-coordinate
if (v1screen.x == v2screen.x && v1screen.y == v2screen.y && v1screen.z < v2screen.z) {
    // if v1.z < v2.z then store v1 in frame-buffer
    ....
}

图 2：三角形表面上像素重叠的点可以通过对构成这些三角形的顶点进行插值来计算

我们想要渲染的是三角形，而不是顶点。 那么问题来了，我们刚刚学到的方法如何应用于三角形呢？ 简而言之，我们将使用三角形顶点坐标来查找像素重叠的三角形上的点的位置（因此它是 z 坐标）。 这个想法如图 2 所示。如果一个像素与两个或多个三角形重叠，我们应该能够计算像素重叠的三角形上的点的位置，并使用这些点的 z 坐标，就像我们处理顶点，以了解哪个三角形距离相机最近。 该方法将在后面文章详细描述。

3、屏幕空间也是三维的

图 3：屏幕空间是三维的（中图）

总而言之，要从相机空间到屏幕空间（这是发生透视划分的过程），我们需要：

• 执行透视除法：即将相机空间 x 和 y 坐标中的点除以点 z 坐标：

• 但还将投影点 z 坐标设置为原始点 z 坐标（相机空间中的点）：

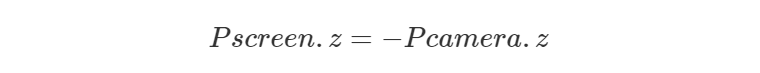
实际上，这意味着我们的投影点不再是 2D 点，而是 3D 点。 或者换句话说，屏幕空间不是二维的。 埃德-卡特穆尔在他的论文中写道：

屏幕空间也是三维的，但对象已经经历了透视变形，因此对象在 x-y 平面上的正交投影将产生预期的透视图像。 — Ed-Catmull 的论文，1974

你现在应该能够理解这句话了。 图 3 还说明了该过程。首先，在相机空间中定义几何顶点（上图）。 然后，每个顶点都会经历透视划分。 也就是说，顶点 x 坐标和 y 坐标除以它们的 z 坐标，但如前所述，我们还将生成的投影点 z 坐标设置为原始顶点 z 坐标的倒数。 顺便说一句，这意味着屏幕空间坐标系的 z 轴方向发生了变化。

正如你所看到的，z 轴现在指向内而不是向外（图 3 中的中间图像）。 但最需要注意的是，生成的对象是原始对象的变形版本，而是三维对象。 此外，Ed-Catmull 所写的“将对象正交投影到 x-y 平面上，将产生预期的透视图像”时的意思是，一旦对象位于屏幕空间中，如果我们追踪垂直于 x-y 图像平面的从对象到画布的线 ，然后我们得到该对象的透视表示（如图 4 所示）：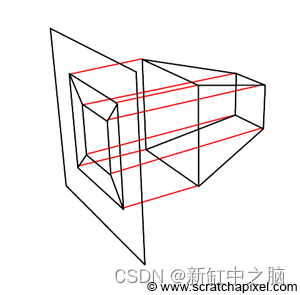

图 4：我们可以通过投影与 x-y 图像平面正交的线，在屏幕空间中形成对象的图像。

这是一个有趣的观察，因为它意味着图像创建过程可以被视为透视投影和正交投影。 如果你不清楚透视和正交投影之间的区别，请不要担心。 这是下一课的主题。 不过，请尝试记住这一观察结果，因为稍后它会变得很方便。

4、将屏幕空间坐标重新映射到 NDC 空间

在前两课中，我们解释了一旦进入屏幕空间，投影点的 x 和 y 坐标需要重新映射到 NDC 空间。 在前面的课程中，我们还解释了在 NDC 空间中，画布上的点的 x 和 y 坐标包含在 [0,1] 范围内。 但在 GPU 世界中，NDC 空间中的坐标包含在 [-1,1] 范围内。 可悲的是，这又是我们需要处理的惯例之一。 我们本可以保留约定 [0,1]，但由于 GPU 是光栅化的参考，因此最好坚持该术语在 GPU 世界中的定义方式。

你可能想知道为什么我们不首先使用 [-1,1] 约定。 有几个原因。 一次是因为我们认为术语“归一化”应该始终表明正在归一化的值在 [0,1] 范围内。 另外，因为很高兴知道多个渲染系统在 NDC 空间概念方面使用不同的约定。 例如，RenderMan 规范将 NDC 空间定义为在 [0,1] 范围内定义的空间。

因此，一旦将点从相机空间转换为屏幕空间，下一步就是将它们分别从 x 坐标和 y 坐标的范围 [l,r] 和 [b,t] 重新映射到范围 [- 1,1]。 术语 l、r、b 和 t 与画布的左、右、下和上坐标相关。 通过重新排列各项，我们可以轻松找到执行我们想要的重新映射的方程：

其中 x 是屏幕空间中 3D 点的 x 坐标（请记住，从现在开始，我们将假设屏幕空间中的点是三维的，如上所述）。 如果我们从方程中删除 l 项，我们会得到：

将所有项除以 (r-l) 我们得到：

我们现在可以展开方程中间的项：

现在我们可以将所有项乘以 2：

我们现在从所有项中删除 1：

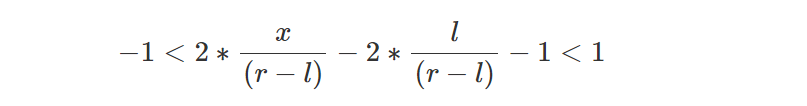
如果我们展开并将重新组合，最终会得到：

这是一个非常重要的方程，因为公式中间方程的红色项和绿色项将成为透视投影矩阵的系数。 我们将在下一课中研究这个矩阵。 但现在，我们只需应用此方程将屏幕空间中的点的 x 坐标重新映射到 NDC 空间（在 NDC 空间中定义时，画布上的任何点的坐标都包含在 [-1.1] 范围内） 。 如果我们对 y 坐标应用相同的推理，我们会得到：

5、整合在一起

在本课程结束时，我们现在可以执行光栅化算法的第一阶段，可以将其分解为两个步骤：

• 将相机空间中的点转换为屏幕空间。 它本质上是将一个点投影到画布上，但请记住，我们还需要存储原始点的 z 坐标。 屏幕空间中的点是树维的，z 坐标将有助于解决稍后的可见性问题。
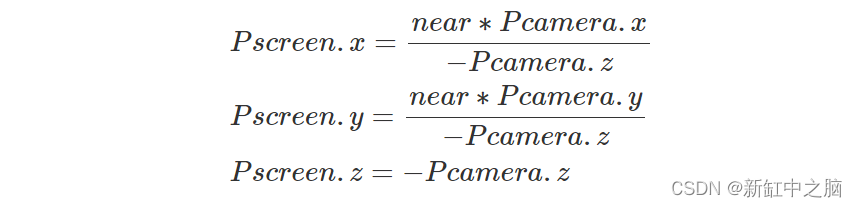
• 然后，我们使用以下公式将屏幕空间中这些点的 x 和 y 坐标转换为 NDC 空间：

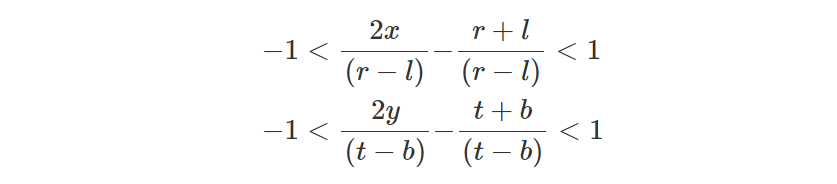
其中l、r、b、t表示画布的左、右、下、上坐标。

将坐标转换为光栅空间非常简单。 我们只需将 NDC 空间中的 x 和 y 坐标重新映射到范围 [0,1] 并将结果数字分别乘以图像宽度和高度（不要忘记在光栅空间中 y 轴向下） 而在 NDC 空间中它会上升。因此我们需要在这个重新映射过程中改变 y 的方向）。 在代码中我们得到：

float nearClippingPlane = 0.1;
// point in camera space
Vec3f pCamera;
worldToCamera.multVecMatrix(pWorld, pCamera);
// convert to screen space
Vec2f pScreen;
pScreen.x = nearClippingPlane * pCamera.x / -pCamera.z;
pScreen.y = nearClippingPlane * pCamera.y / -pCamera.z;
// now convert point from screen space to NDC space (in range [-1,1])
Vec2f pNDC;
pNDC.x = 2 * pScreen.x / (r - l) - (r + l) / (r - l);
pNDC.y = 2 * pScreen.y / (t - b) - (t + b) / (t - b);
// convert to raster space and set point z-coordinate to -pCamera.z
Vec3f pRaster;
pRaster.x = (pNDC.x + 1) / 2 * imageWidth;
// in raster space y is down so invert direction
pRaster.y = (1 - pNDC.y) / 2 * imageHeight;
// store the point camera space z-coordinate (as a positive value)
pRaster.z = -pCamera.z;

请注意，栅格空间中的点或顶点的坐标此处仍定义为浮点数，而不是整数（像素坐标的情况就是如此）。

6、下一步是什么？

现在，我们已将三角形投影到画布上，并将这些投影顶点转换为光栅空间。 三角形的顶点和像素都位于同一坐标系中。 我们现在准备循环图像中的所有像素，并使用一种技术来查找它们是否与三角形重叠。 这是下一章的主题。

---

原文链接：光栅化投影阶段算法 - BimAnt