二叉搜索树相关问题

二叉搜索树（Binary Search Tree）是特殊的二叉树，其构建的规则符合：左孩子节点值小于根节点值，右孩子节点值大于根结点值（严格的BST树是不存在两个相同值的节点的），这种规则使得BST树的中序遍历为升序状态。接下来的题目笔记是我在leetcode中刷题遇到的二叉搜索树相关的题目，题目的讲解看一看代码随想录。这些题目里面最近公共祖先问题和二叉搜索树中的插入问题是最值得值得关注的（前者面试高频考点，后者为难度较其他题目高）

https://programmercarl.com/

1.二叉搜索树中搜索

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root == nullptr) return NULL;
        if(root->val == val){
            return root;
        }else if(root-> val >val){
           return searchBST(root->left, val);
        }else{
            return searchBST(root-> right,val);
        }
    }
};

2.验证二叉搜索树

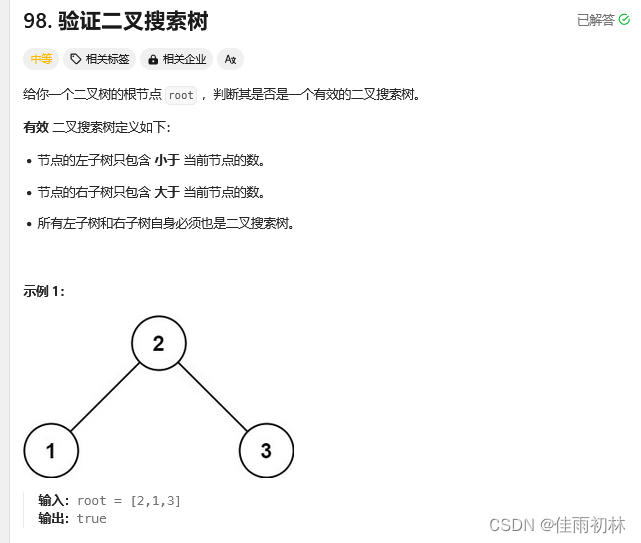
class Solution {
public:
    //BST的中序遍历是一个有序的数组
    vector<int> visit;
    void dfs(TreeNode* root){
        if(root==nullptr) return;
        dfs(root->left);
        visit.push_back(root->val);
        dfs(root->right);
    }
    bool isValidBST(TreeNode* root) {
        dfs(root);
        for(int i = 0; i < visit.size() - 1; i++){
            if(visit[i+1]<=visit[i]) return false;
        }
        return true;
    }
};

3.二叉搜索树的最小绝对差

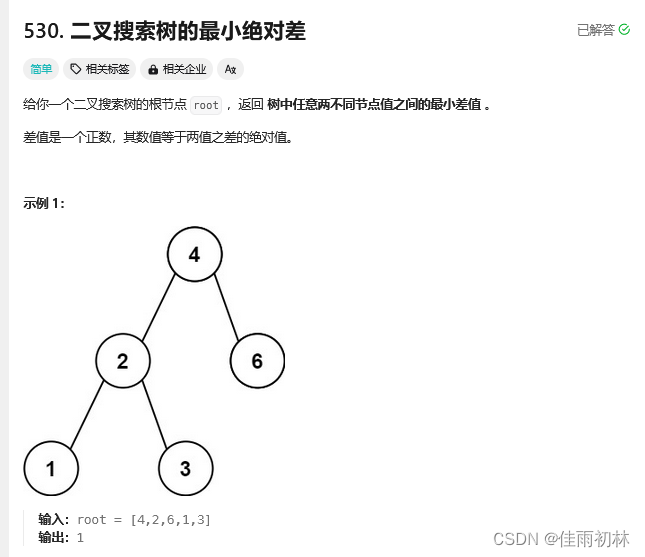
class Solution {
public:
    vector<int> visit;
    void dfs(TreeNode* root){
        if(root==nullptr) return;
        dfs(root->left);
        visit.push_back(root->val);
        dfs(root->right);
    }
    int getMinimumDifference(TreeNode* root) {
        dfs(root);
        sort(visit.begin(), visit.end());
        int ans = visit[1] - visit[0];
        for(int i = 2; i < visit.size(); i++){
            ans = min(ans, visit[i] - visit[i - 1]);
        }
        return ans;
    }
};

4.二叉搜索树中的众数

class Solution {
private:

    void searchBST(TreeNode* cur, unordered_map<int, int>& map){//前序遍历
        if(cur == NULL) return;
        map[cur->val]++; //统计元素频率
        searchBST(cur->left, map);
        searchBST(cur->right, map);
    }
    bool static cmp(const pair<int, int>& a, const pair<int, int>& b){
        return a.second > b.second;
    }
public:
    vector<int> findMode(TreeNode* root) {
        unordered_map<int, int> map; 
        vector<int> result;
        if(root == nullptr) return result;
        searchBST(root,map);
        vector<pair<int, int>> vec(map.begin(), map.end());
        sort(vec.begin(), vec.end(), cmp);//给频率排序
        result.push_back(vec[0].first);
        for(int i = 1; i< vec.size(); i++){
            //取最高的放到result中
            if(vec[i].second == vec[0].second) result.push_back(vec[i].first);
            else break;
        }
        return result;
    }
};

5.最近公共祖先问题（LCA）

5.1二叉树的最近公共祖先

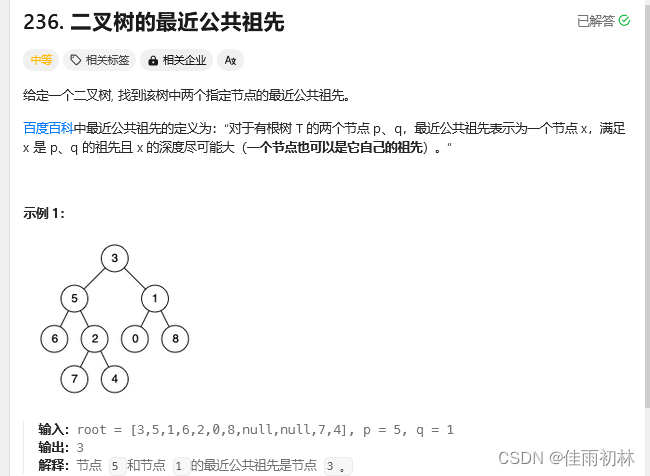
解法一：递归实现

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //当找到目标节点时返回该节点（为空时也返回）
        if(root == nullptr || root == p || root == q) return root;
        TreeNode* leftNode = lowestCommonAncestor(root->left, p, q);
        TreeNode* rightNode = lowestCommonAncestor(root->right, p, q);
        if(leftNode != nullptr && rightNode != nullptr) return root;
        if(leftNode == nullptr) return rightNode;
        return leftNode;
    }
};

解法二：Hash

class Solution {
public:
    unordered_map<int, TreeNode*> fa;
    unordered_map<int, bool>vis;
    void dfs(TreeNode* root){
        if(root->left != nullptr){
            fa[root->left->val] = root;
            dfs(root->left);
        }
        if(root->right != nullptr){
            fa[root->right->val] = root;
            dfs(root->right);
        }
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //先将根节点（其父节点为空）存入到map中
        fa[root->val] = nullptr;
        //构建整棵树的父节点的map（node->val, node的父节点）
        dfs(root);
        while(p != nullptr){
            //将p节点的标记为已访问的状态
            vis[p->val] = true;
            //用p节点的父节点替换p（模拟朝着祖先节点靠近的过程）
            p = fa[p->val];
        }
        while(q != nullptr){
            //q也沿着祖先走，遇到第一个已被访问过的祖先就是LCA
            if(vis[q->val]) return q;
            q = fa[q->val];
        }
        return nullptr;
    }
   
};

5.2二叉搜索树最近公共祖先

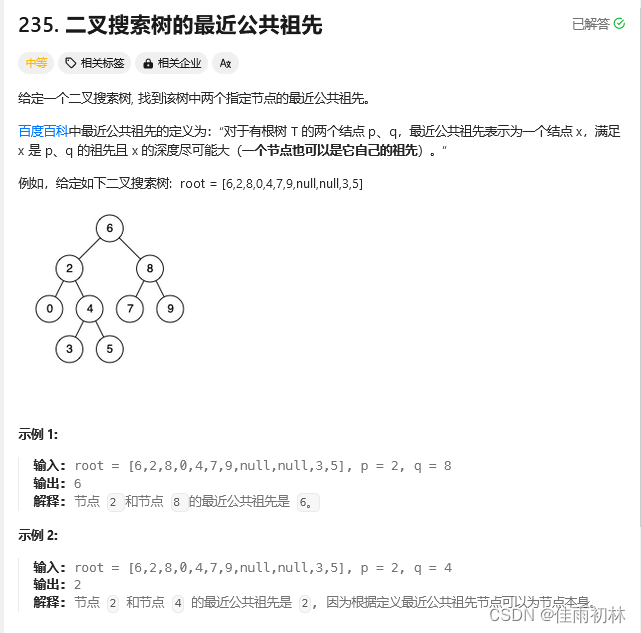
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root->val > p->val && root->val > q->val){
            return lowestCommonAncestor(root->left, p, q);
        }else if(root->val < p->val && root->val < q->val){
            return lowestCommonAncestor(root->right, p, q);
        }else{
            return root;
        }
    }
};

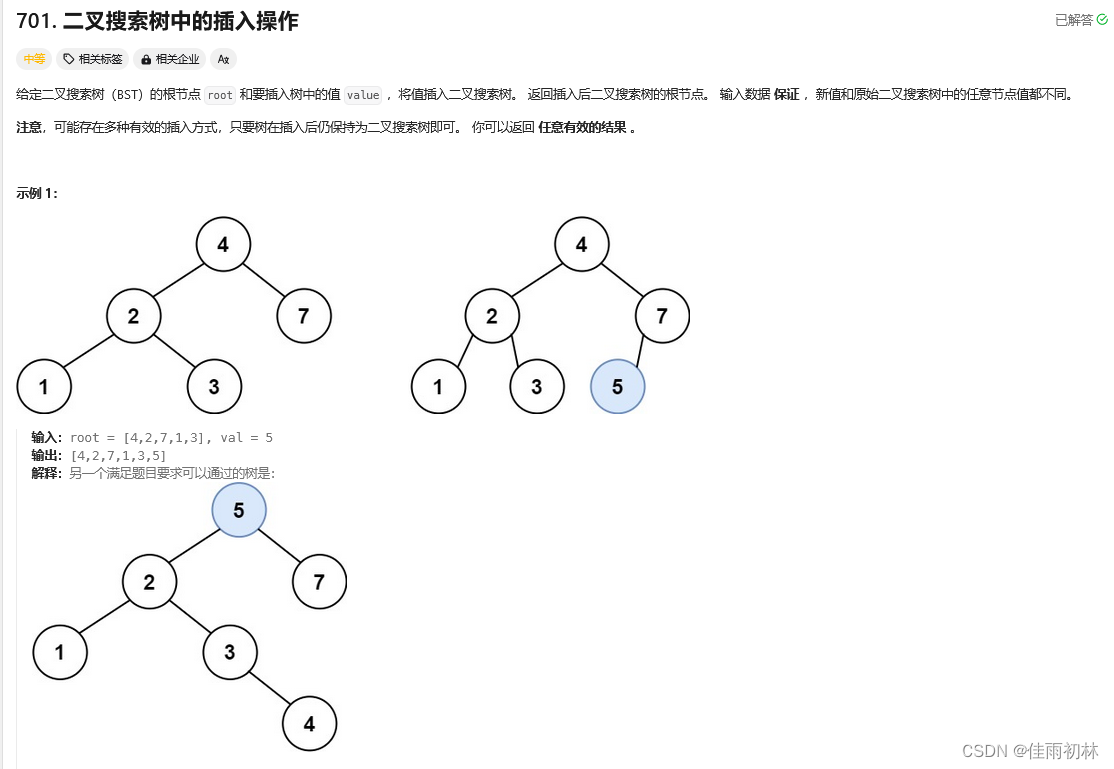
6.二叉搜索树中的插入操作

class Solution {
public:
    TreeNode* parent;
    void travel(TreeNode* cur, int val){
        if(cur == nullptr){
            TreeNode* node = new TreeNode(val);
            if(val > parent->val) parent->right = node;
            else parent->left = node;
            return;
        }
        parent = cur;
        if(cur->val > val) travel(cur->left, val);
        if(cur->val < val) travel(cur->right, val);
        return;
    }
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if(root == nullptr) root = new TreeNode(val);
        travel(root, val);
        return root;
    }
};

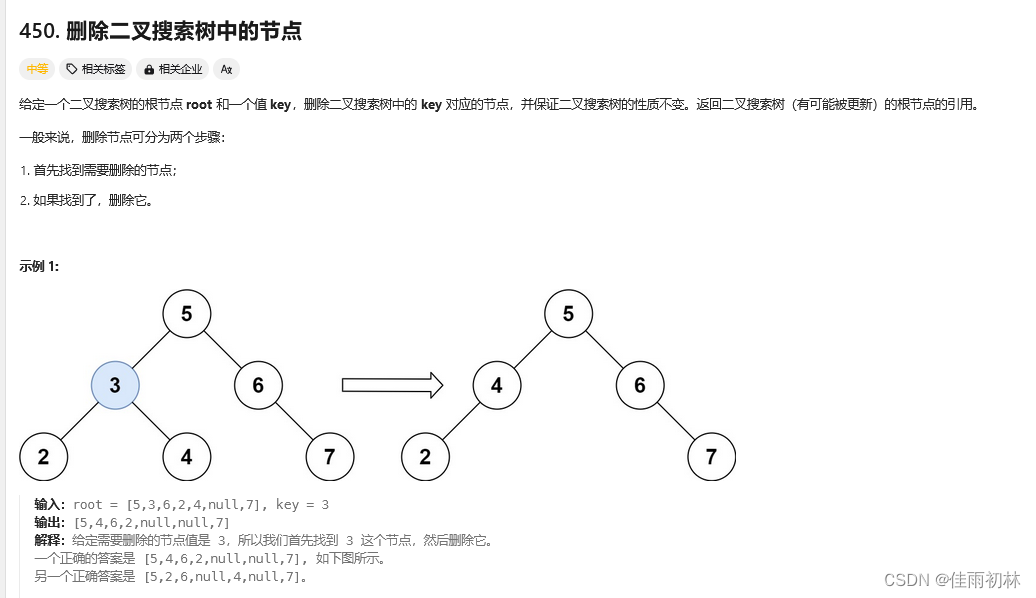
7.删除二叉搜索树中的节点

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(root == nullptr) return nullptr;
        if(key > root->val) root->right = deleteNode(root->right, key);//去右子树删除
        else if(key < root->val) root->left = deleteNode(root->left, key);//去左子树删除
        else{ //当前节点就是要删除的节点
            if(!root->left) return root->right;//情况1：要删除的节点无左子
            if(!root->right) return root->left;//情况2：要删除的节点无右子
            TreeNode* node = root->right;      //情况3：要删除的节点左右孩子都有
            while(node->left){//寻找要删除节点右子树的最左节点
                node = node->left;
            }
            node->left = root->left;//将要删除节点的左子树成为其右子树的最左节点的左子树
            root = root->right;//将要删除节点的右孩子顶替其位置，节点被删除
        }
        return root;
    }
};

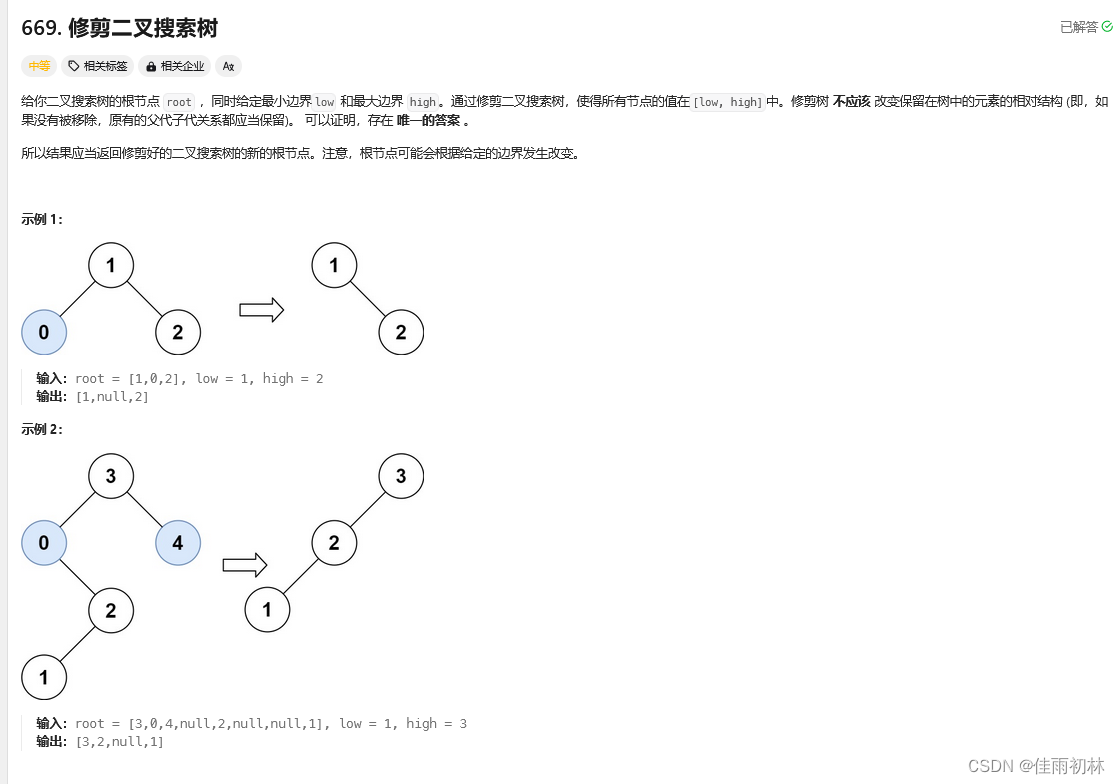
8.修剪二叉搜索树

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(root == nullptr) return nullptr;
        if(root->val < low){
            TreeNode* right = trimBST(root->right, low, high);
            return right;
        }
        if(root->val > high){
            TreeNode* left = trimBST(root->left, low, high);
            return left;
        }
        root->left = trimBST(root->left, low, high);
        root->right = trimBST(root->right, low, high);
        return root;
    }
};

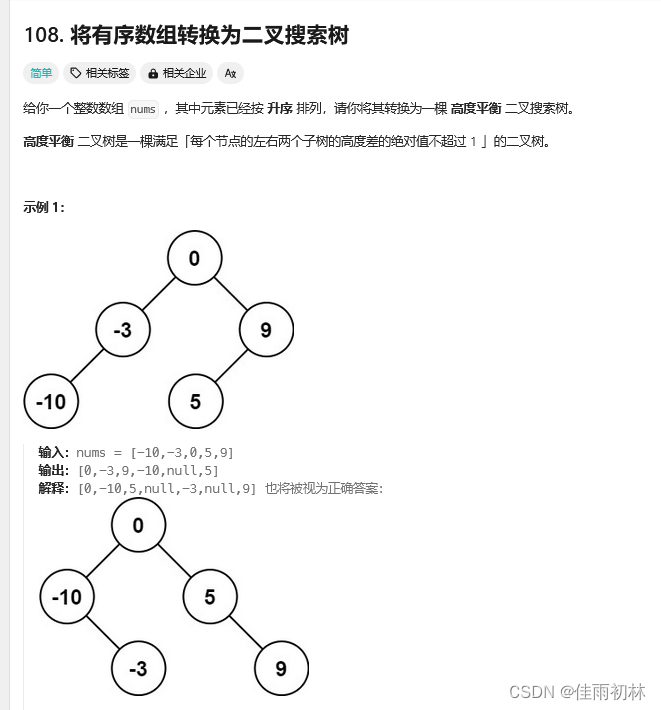
9.将有序数组转化为二叉搜索树

class Solution {
public:
    TreeNode* root;
    //左闭右闭区间
    TreeNode* TreeBuild(vector<int>& nums, int begin, int end){
        if(begin > end) return NULL;
        int mid = (begin + end)>>1;
        TreeNode* node = new TreeNode(nums[mid]);
        node->left = TreeBuild(nums, begin, mid - 1);
        node->right = TreeBuild(nums, mid + 1, end);
        return node; 
    }
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return TreeBuild(nums, 0, nums.size() - 1);
    }
};

10.把二叉搜索树转化为累加树

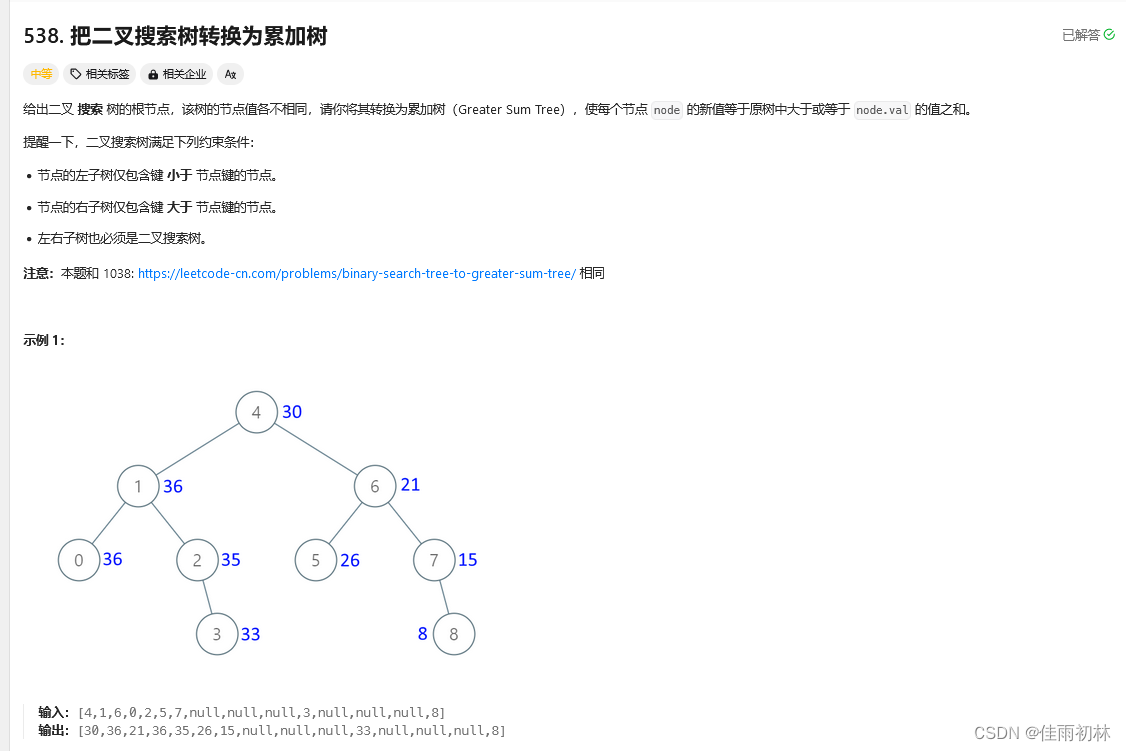
class Solution {
public:
    int pre = 0; //记录前一个节点的数值
    void travel(TreeNode* root){
        if(root == nullptr) return;
        travel(root->right);
        root->val += pre;
        pre = root->val;
        travel(root->left);
    }
    TreeNode* convertBST(TreeNode* root) {
        travel(root);
        return root;
    }
};