递归-全排列和组合的输出模版

这一篇文章主要介绍两个模版，做题中经常会有这种模版的出现所以可以浅浅记一下~~

例如：

P1036

[NOIP2002 普及组] 选数

P2089

烤鸡

全排列：

题目：

代码思路：

1、前部分：递归出口当前我要求的搭配方案里的元素个数足够：打印输出（数组存储的）

2、中部分：使用for循环从1~n的枚举输入进来的所有元素，但是为了避免元素重复需要一个标记数组记录那些数使用过了，如果没有使用过进入储蓄数组，递归搭配。

代码：

#include<iostream>
#include<cstdio> 
#include<string.h>
using namespace std;

char ans[10000],a[1000]; // ans临时数组用于记录我的搭配，a原数组用来组合搭配。 
char v[10]; //标记我当前这个数是否使用过 
int len; 


void func(int n){
	if(n == len){ //如果n的长度大小和len一样说明取满了输出 
		for(int i = 0; i < len; i++) cout << ans[i];
		cout << endl;
		return;
	}
	for(int i = 0; i < len; i++){
		if(v[i] == 0){ //当前位是否被使用 
			v[i] = 1; //使用后标记 
			ans[n] = a[i]; //存入搭配数组 
			func(n+1); //再搭配剩下的len-n个数 
			v[i] = 0; //再这一次中搭配过得下次依旧可以使用 
		}
	}
}

int main(){
	cin >> a;
	len =  strlen(a);
	func(0);
	return 0;
}

组合输出:

题目：

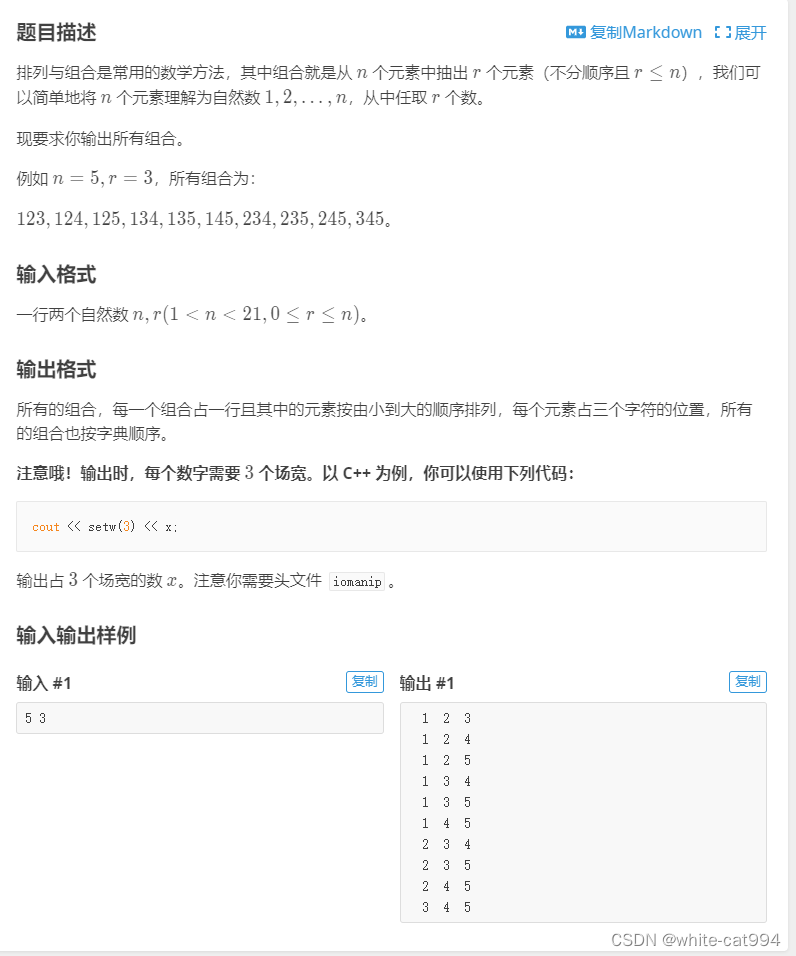
代码思路：

1、前部分：递归出口当前我要求的搭配方案里的元素个数足够：打印输出（数组存储的）

2、中部分：使用for循环从上次看到的位置+1开始寻找下一个元素，元素个数找完为止，不用使用标记数组，因为我从下一个数开始找元素肯定不重复（前提是没有重复的元素在输入的搭配方案可用元素里，例如输入中有两个1,1这样就会有重复）。找到元素存入数组，递归搭配。

代码：

#include<bits/stdc++.h>
using namespace std;
int a[1000];
int n,k;

void func(int m,int idx){
	if(m == k){
		for(int i = 0; i < m; i++) printf("%3d",a[i]);
		cout << endl;
	}
	for(int i = idx+1; i <= n; i++){ //idx为我上次找到元素的位置从后面继续找
		a[m] = i;
		func(m+1,i); //m+1搭配方案里的元素+1，idx=i为我现在看到的元素位置
	}
}

int main(){
	cin >> n >> k;
	func(0,0);
	return 0;
}

区别：

全排列问题：只要排列元素的顺序不同，搭配方案里的元素允许和另一种搭配方案完全相同

例如：1 2 3（三个元素搭配）会有1 2 3 , 1 3 2 ，2 3 1 ，2 1 3 , 3 2 1 , 3 1 2这六种情况

组合输出：搭配方案里的元素不允许和另一种搭配方案完全相同，顺序不一样也不行，只会按照一种来算

例如：1 2 3（三个元素搭配）会有1 2 3这一种情况