二分搜索边界问题的简单结论

引言

二分搜索是一个说简单也很简单（代码很固定，也没几行），说难也很难（边界问题可能会让人想不太清楚）。
事实上，边界问题也是是算法题中普遍存在的难点。
这篇文章讲两个简单的结论，来轻松解决二分搜索算法中的两个边界问题。

Demo1

    /**
     * 普通二分搜索java实现
     * 在数组nums中找target。如果能找到，返回数组下标。如果找不到返回-1
     * @param nums      搜索对象
     * @param target    目标值
     * @return
     */
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        while(left <= right) {
            int mid = left + (right - left >> 1);//等效：int mid = (left + right)/2
            if (target < nums[mid]) {
                right = mid - 1;
            } else if (target > nums[mid]) {
                left = mid + 1;
            } else {
                return mid;
            }
        }
        return -1;
    }

这是二分搜索最基础的一段代码。
虽然很简单，但这却是所有二分搜索的基本逻辑。大部分变体都和上面这段代码大差不差。
但其中的边界问题需要想清楚。

循环边界问题

• 定义右指针时，右边界是开还是闭？
  int right = nums.length;
  or
  int right = nums.length - 1;
• 循环要不要等号？
  while(left <= right)
  or
  while(left < right)

这里给一个一劳永逸的答案，就按照上面的demo，选择：左闭右闭
原因很简单：两边都有效，最容易思考。
当选择左闭右闭后，while循环就得加上等号
因为：如果选择不加等号，假如数组里只有一个元素，此时根本无法进入while循环。

Demo2

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。
如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

这个题也不难，很多人都能做出来。
但多少人能肯定自己在做这个题时候没有“猜”的成分？
可以肯定的给出一个让人信服且易于理解的解释。

循环结束，两个指针停在哪里

这个题可以分为两部分：

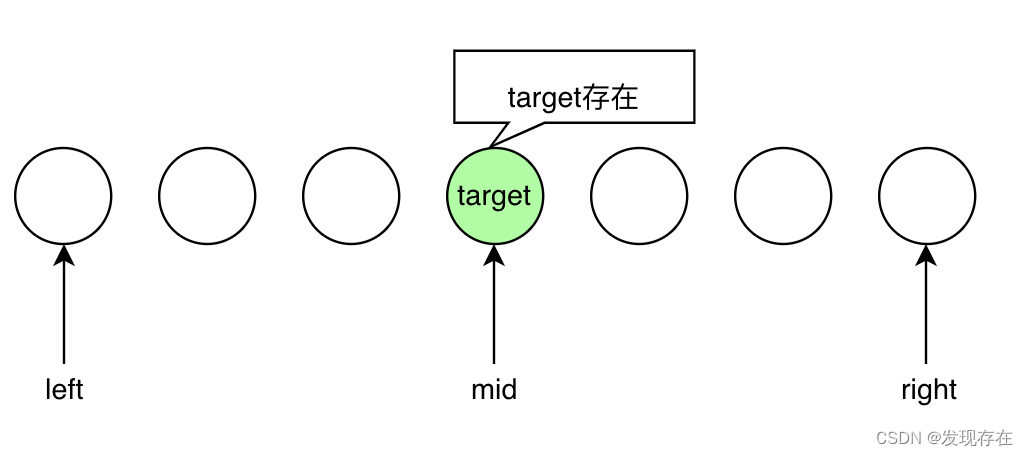
1. 能找到target，就像demo1那样：通过mid匹配上target，然后直接返回。此时我们确实不需要关心最后左右指针停在哪里，如下图所示（mid直接找到了绿色的target）
   
2. target不存在。这是这个题的关键难点所在。
   虽然我们大致知道写出来的最终代码和上面的demo区别依然不大，但是是+1还是-1，是谁+1？left+1？ right+1？ or mid+1？这个边界问题就有点让人头疼了。
   假如我们知道左右指针最终停的位置，这个问题就会被大大简化。

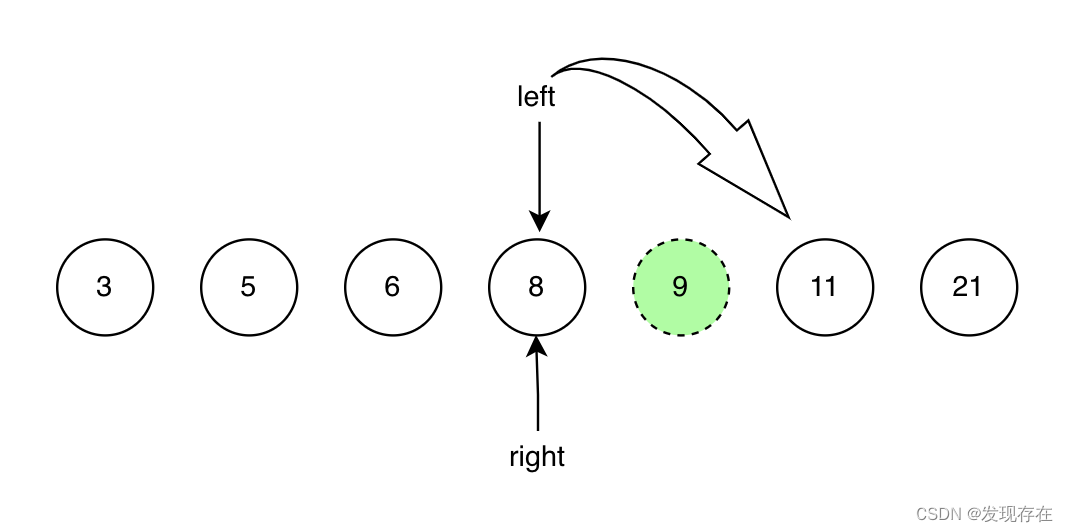
直接给出结论：左右指针停在“这个不存在的target”的右左两边。如下图所示

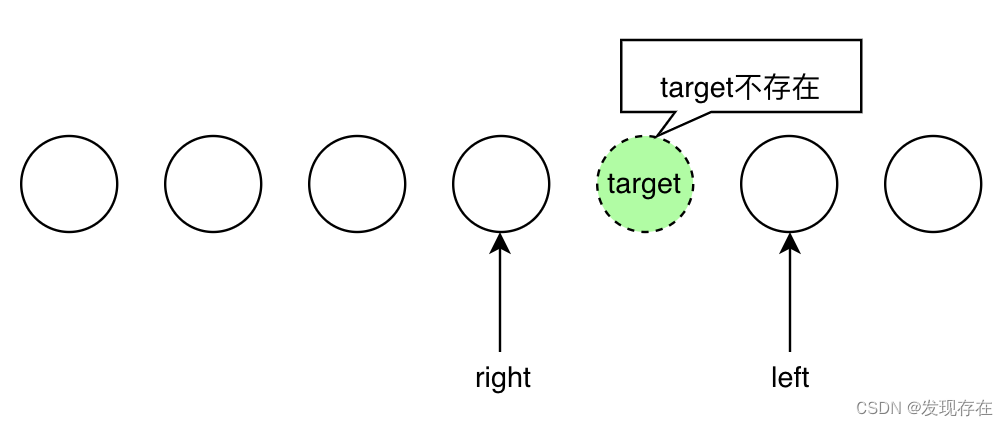
绿色的target并不存在，也就是说两个指针其实是前后挨着的，中间并没有元素，只不过 左指针在右边，右指针在左边。

依据这样一个简单的结论，解决上面的问题就很简单了，一目了然：当target不存在时，left指针的位置就是大于target的最小值。

Demo2答案

public int searchInsert(int[] nums, int target) {
     int start = 0;
     int end = nums.length-1;
     while (start <= end) {
         int mid = ((end - start) >> 1) + start;
         if (nums[mid] == target) {
             return mid;
         } else if (nums[mid] > target) {
             end = mid - 1;
         } else {
             start = mid + 1;
         }
     }
     return start;
 }

根据这个直观的直观的简单结论，还可以轻松解决很多二分搜索是变体问题。

注意两端别越界

1. target比最小的值还小时：
   
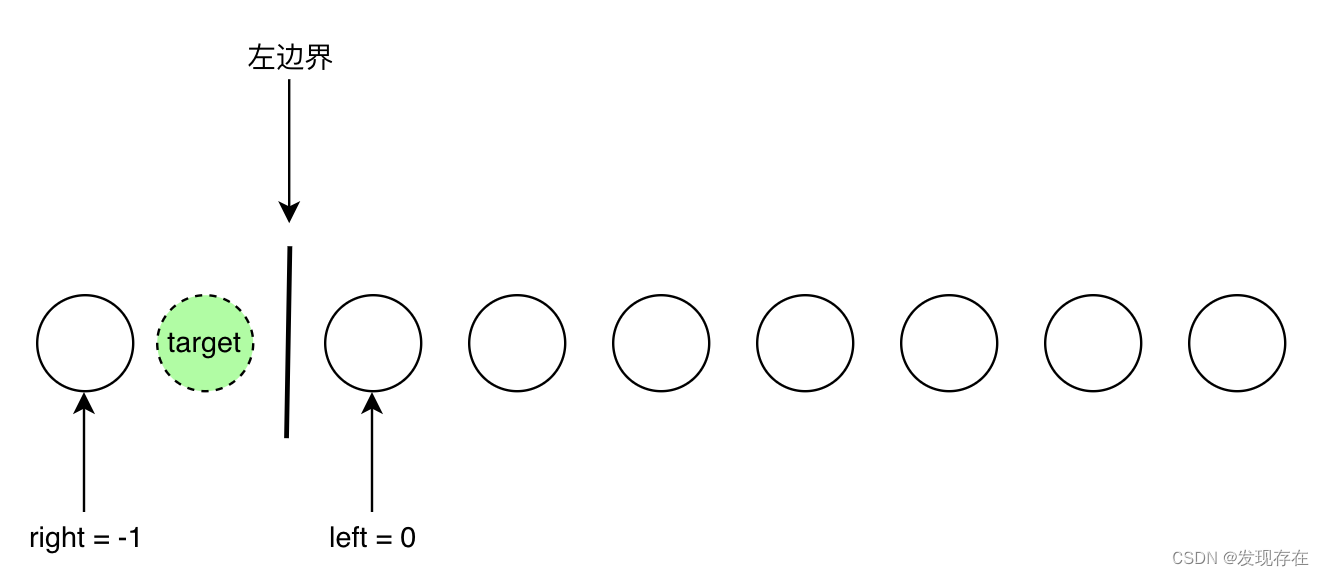
   此时right就越界了。如果最终要使用right，可能就需要先判断一下。
2. target比最大的值还大：
   
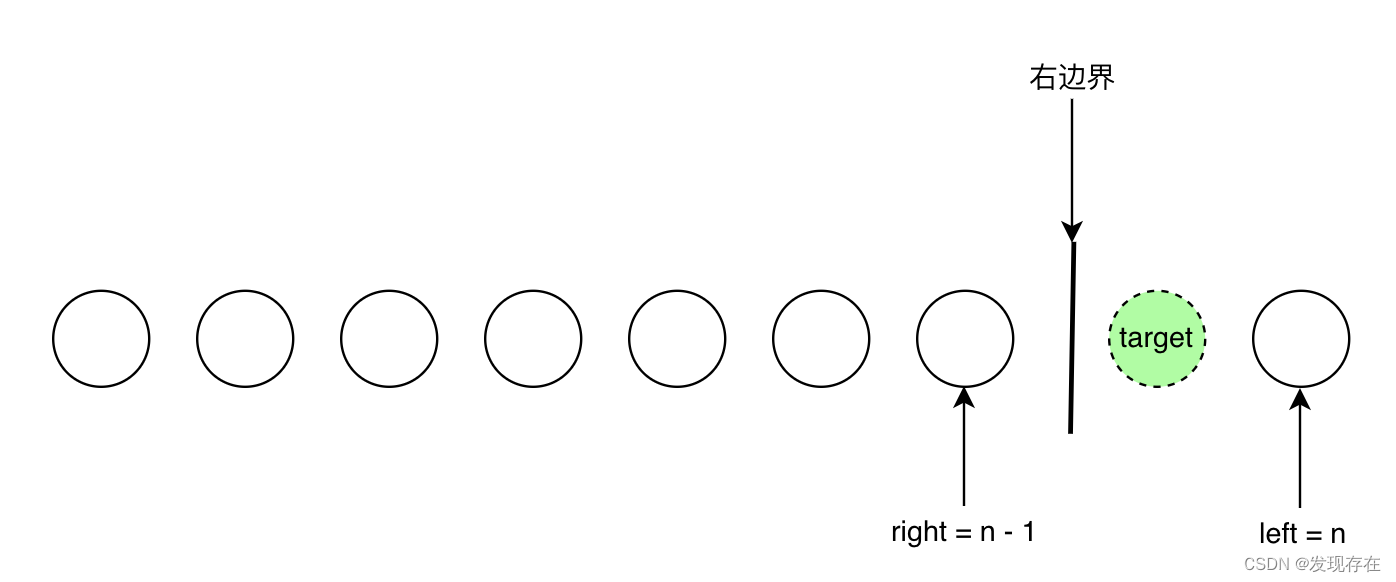
   此时left越界，同样在使用时要注意判断。
   其实Demo2返回的就是left，为什么不担心越界？
   因为题目的要求是：
   如果目标值不存在于数组中，返回它将会被按顺序插入的位置
   如果target很大，超过了所有值，需要返回的就是n。

为什么

通过观察Demo的执行逻辑，我们可以发现。
如果target不存在，必然会循环到结束。而在最后一次循环中，当left==right，此时两个指针所在的值 无论比target大还是比 target小，下一步肯定有一个指针要再挪动一步。如图所示

总结

• 二分法固定写法：左闭右闭，while加等号
• 当target不存在时，左右指针最终停在“target的右左两边”