统计学-R语言-4.6

---

前言

本篇文章是对数据可视化的补充文章。

---

列联表

跳转至该篇博客
跳转至该篇博客

在上面两篇博客中，对单变量和双变量的列联表进行了实例展示，下面是对三维列联表进行实例。
行变量为被调查者所属社区和性别，列变量为态度的三维列联表：

load("C:/example/ch2/example2_1.RData")
mytable1<-ftable(example2_1);mytable1

生成行变量为被调查者性别和态度，列变量为社区的三维列联表：

mytable2<-ftable(example2_1,row.vars=c("性别","态度"),col.var ="社区")
mytable2

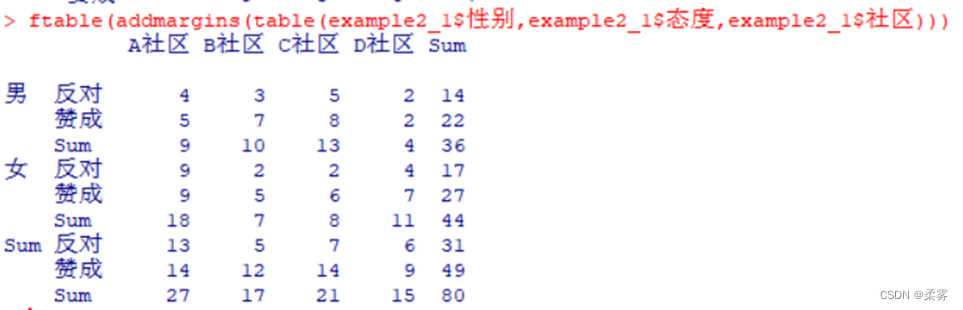
为列联表mytable2增加边际和：

ftable(addmargins(table(example2_1$性别,example2_1$态度,example2_1$社区)))

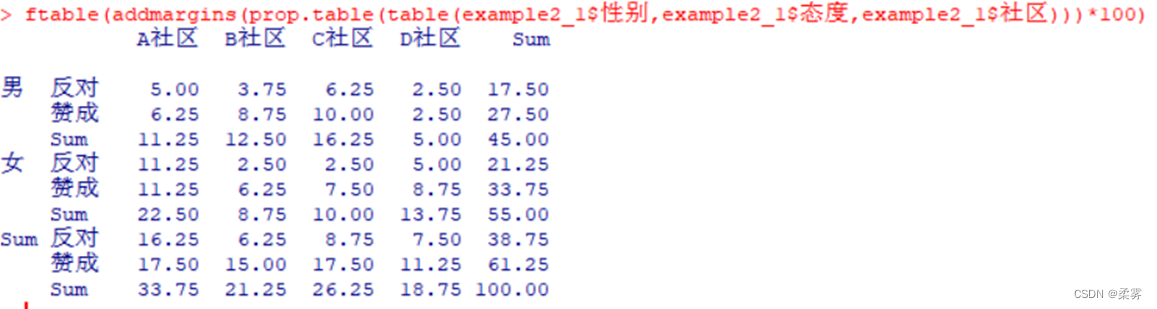
将列联表mytable2转化为百分比表：

ftable(addmargins(prop.table(table(example2_1$性别,example2_1$态度,example2_1$社区)))*100)

函数ftable（x，…）用于产生扁平化列联表。参数x为一个列表、数据框或列联表对象。ftable（x）按x中变量的原始排列顺序列表，将最后一个变量作为列变量，如 mytable1. ftable（x，row.vars，col.var)可以改变变量的列表方式，如mytable2。

例题：
一家购物网站连续120天的销售额数据。生成一张频数分布表观察销售额的分布特征。

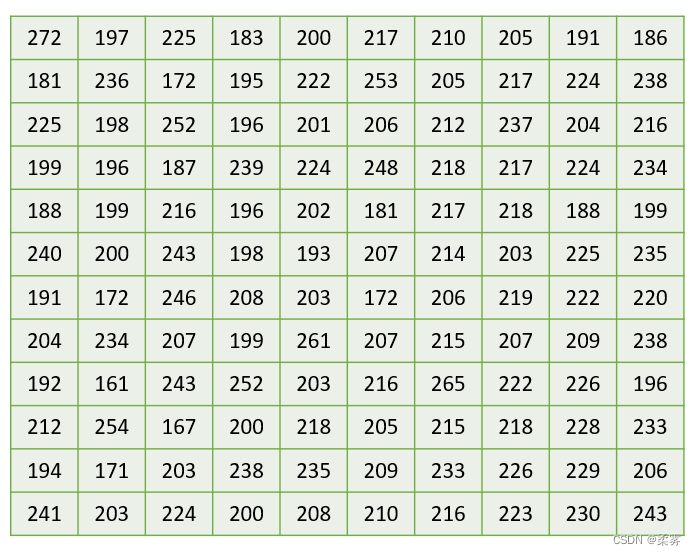
首先，确定组数。组数的多少与数据本身的特点及数据的多少有关。组数的确定方法有多种。设组数为K，根据 Sturges提供的方法确定组数。K=1+lg(n)/lg(2)当然这只是个大概数，具体的组数可根据需要做适当调整。本例共有120个数据，组数K=1+lg（120）/lg（2）=8（或使用R函数 nclass. Sturges（example2_2$销售额），得K=8），为便于理解，这里分为12组。
其次，确定各组的组距。组距可根据全部数据的最大值和最小值及所分的组数来确定。即组距=（最大值一最小值）÷组数。对于本例数据，最大值为272，最小值为161，则组距=（272-161）÷12=9.25。为便于计算，组距宜取5或10的倍数，因此组距可取10。为避免数据被遗漏，第一组的下限应低于最小数值，最后一组的上限应高于最大数值。
最后，统计出各组的频数即得频数分布表。在统计各组频数时，恰好等于某一组上限的变量值一般不算在本组内，而算在下一组，即一个组的数值x满足a≤x<b（a为下限值，b为上限值）
round_any( )函数，可以将向量数据近似到任意指定的精度。
生成频数分布表的R代码如下所示：

load("C:/example/ch2/example2_2.RData")
vector2_2<-as.vector(example2_2$销售额)
library(plyr)
count<-table(round_any(vector2_2,10,floor))
count<-as.numeric(count)
pcount<-prop.table(count)*100
cumsump<-cumsum(pcount)
name<-paste(seq(160,270,by=10),"-",seq(170,280,by=10),sep="")
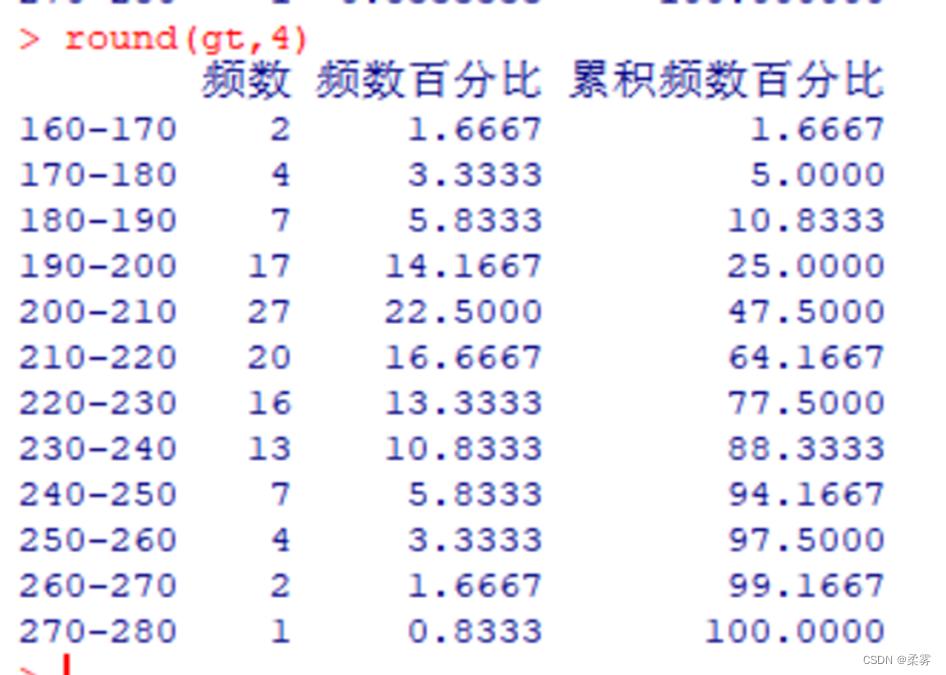
gt<-data.frame("频数"=count,"频数百分比"=pcount,"累积频数百分比"=cumsump,row.names=name)
round(gt,4)#函数round（x， digits）是对数据x按digit照指定的精度改变输出的小数位.本例将输出结果保留4位小数.

使用“cut”函数，将【例2—2】分成间隔为10的组（不用考虑组数，有了间隔，组数自然就确定了）

load("C:/example/ch2/example2_2.RData")
vector2_2<-as.vector(c(example2_2$销售额))
d<-table(cut(vector2_2,breaks=10*(16:28),right=FALSE))
dd<-data.frame(d)
percent<-dd$Freq/sum(dd$Freq)*100
cumsump<-cumsum(percent)
df<-data.frame(dd,percent,cumsump)
library(reshape)
mytable<-rename(df,c(Var1="分组",Freq="频数",percent="频数百分比",cumsump="累积频数百分比"))
mytable

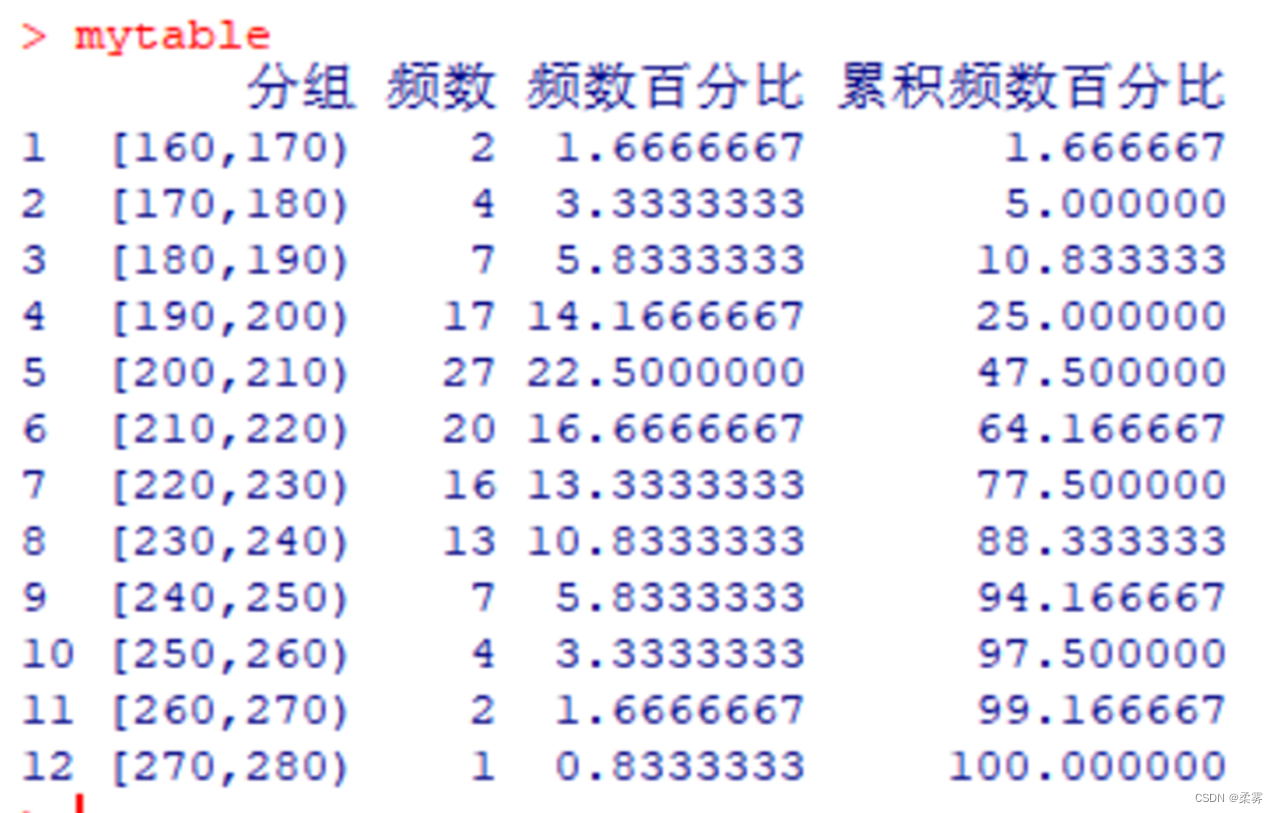
函数cut（x， breaks， right=true，dig.ab=3，）中，x为数值向量。 breaks为要分的组数。例如：breaks=5表示分成5组， breaks=10*（5：10）表示将50~100之间的数据分成间隔为10的组。一般， breaks=k*(x1：x2）表示以k为组的间隔，kx1应小于等于数据集的最小值，kx2应大于数据集的最大值。而且，k与x1、k与x2之间应为整数倍的关系。默认 right=TRUE，表示封闭上限（即含上限值），设定 right=FALSE，则表示不封闭上限（即不含上限值）。dig.lab=3表示分组标签默认保留3位数值，可根据需要设定要保留的数值位数。

条形图及其变种—单式条形图

例题2-1：

load("C:/example/ch2/example2_1.RData")
count1<-table(example2_1$社区)
count2<-table(example2_1$性别)
count3<-table(example2_1$态度)
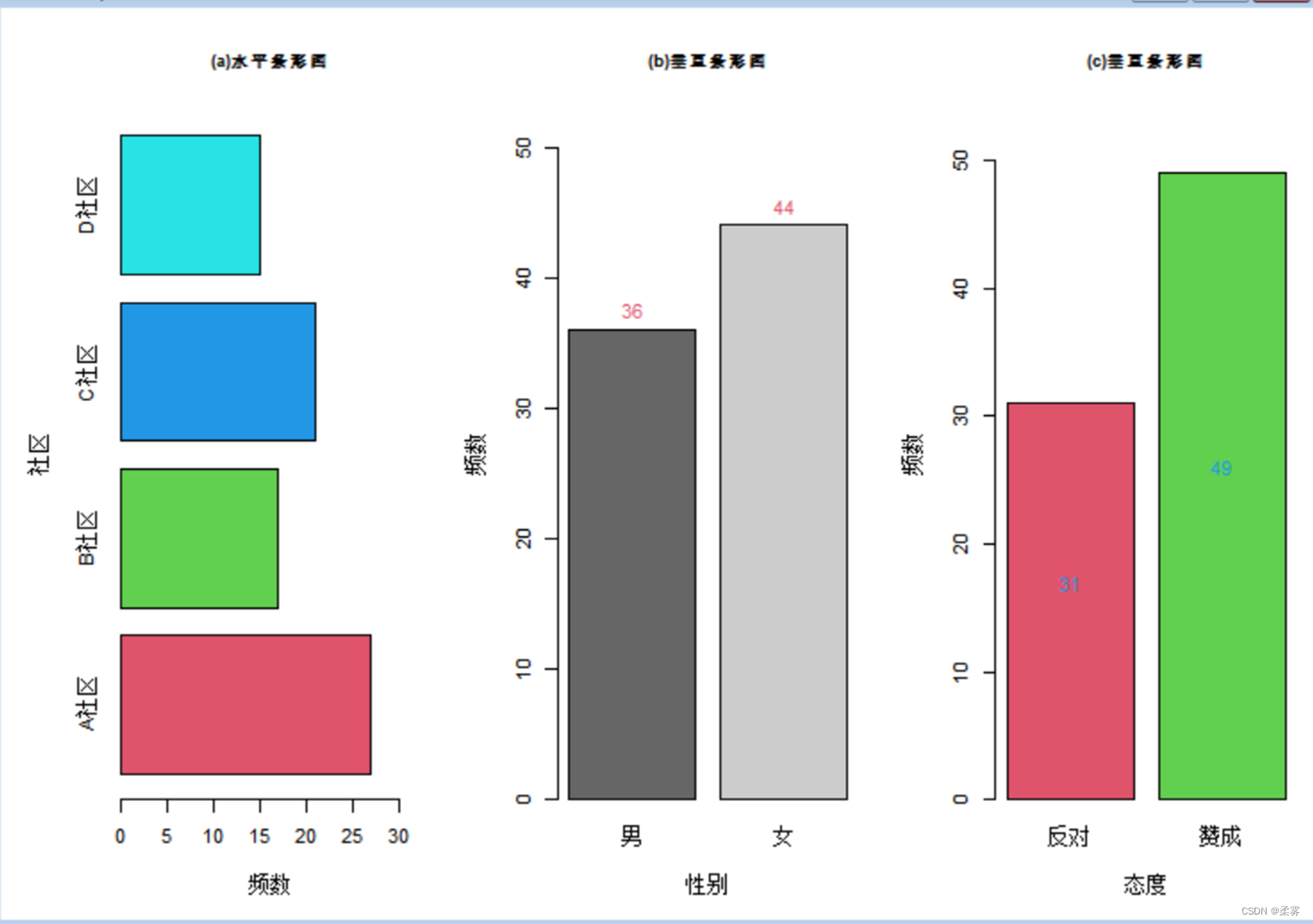
par(mfrow=c(1,3),mai=c(0.7,0.7,0.6,0.1),cex=0.7,cex.main=0.8)
bar<-barplot(count1,xlab="频数",ylab="社区",horiz=TRUE,xlim=c(0,1.2*max(count1)),main="(a)水平条形图",col=2:5)
text(bar,count1,labels=count1,pos=4,adj=c(0,0.5))
bar<-barplot(count2,xlab="性别",ylab="频数",col=c("gray40","gray80"),ylim=c(0,1.2*max(count2)),main="(b)垂直条形图")
text(bar,count2,labels=count2,pos=3,col=2)
bar<-barplot(count3,xlab="态度",ylab="频数",ylim=c(0,1.1*max(count3)),col=2:3,main="(c)垂直条形图")
text(bar,count3/2,labels=count3,pos=3,col=4)

函数 barplot( height，…)创建条形图。参数 height为向量、矩阵、数据框或表格；x1ab="设置x轴标签；y1ab="设置y轴标签； horiz=TRUE绘制水平条形图；col="设置图形颜色；main="为图形增加主标题；sub="为图形。

条形图及其变种—帕累托图

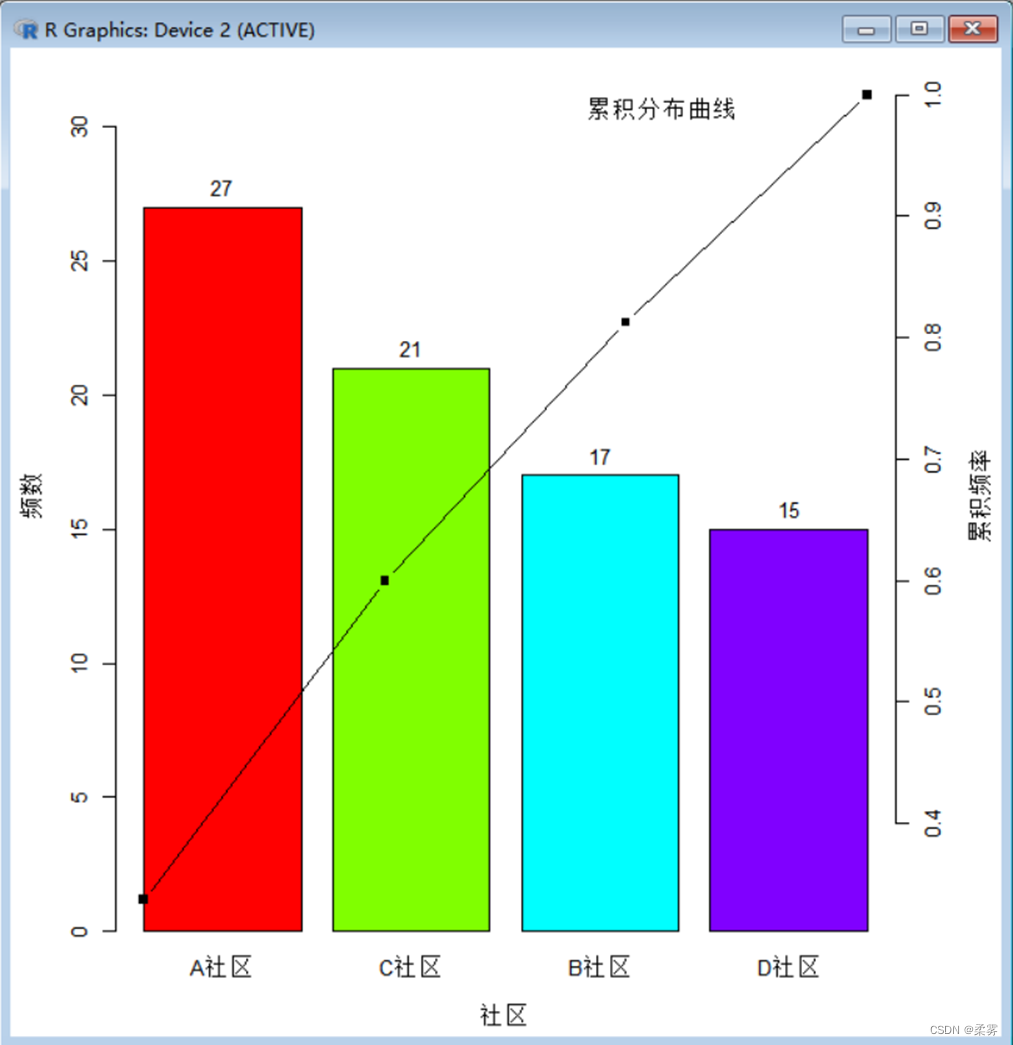
帕累托图( Pareto plot)是以意大利经济学家V. Pareto的名字命名的，它是按各类别的频数多少排序后绘制的条形图。帕累托图可以看作简单条形图的一个变种，利用该图很容易看出哪类频数出现得多，哪类频数出现得少。以例2-1的社区为例，绘制帕累托图的R代码和结果如下所示

# load("C:/example/ch2/example2_1.RData")
count1<-table(example2_1$社区)
par(mai=c(0.7,0.7,0.1,0.7),cex=.8)
x<-sort(count1,decreasing=T)
bar<-barplot(x,xlab="社区",ylab="频数",col=rainbow(4),ylim=c(0,1.2*max(count1)))
text(bar,x,labels=x,pos=3,col=1)
####了解即可
y<-cumsum(x)/sum(x)
par(new=T)
plot(y,type="b",lwd=1.5,pch=15,axes=FALSE,xlab='',ylab='',main='')
axis(4)
mtext("累积频率",side=4,line=3,cex=.8)
mtext("累积分布曲线",line=-2.5,cex=.8,adj=0.75)

条形图及其变种—复式条形图

load("C:/example/ch2/example2_1.RData")
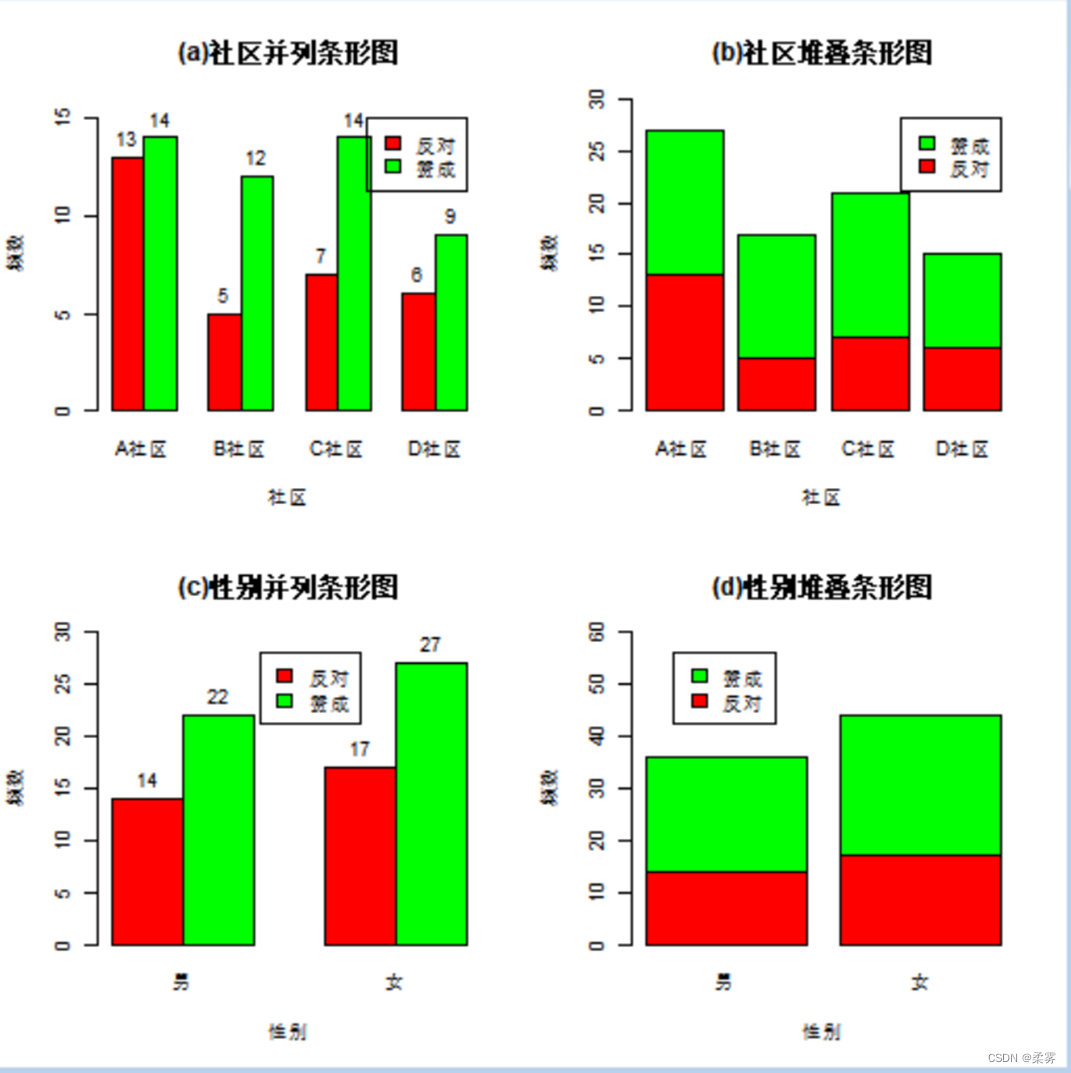
mytable1<-table(example2_1$态度,example2_1$社区)
par(mfrow=c(2,2),cex=0.6)
bar1<-barplot(mytable1,xlab="社区",ylab="频数",ylim=c(0,16),col=c("red","green"),legend=rownames(mytable1),args.legend=list(x=12),beside=TRUE,main="(a)社区并列条形图")
text(bar1,mytable1,labels=mytable1,pos=3,col=1)
bar2<-barplot(mytable1,xlab="社区",ylab="频数",ylim=c(0,30),col=c("red","green"),legend=rownames(mytable1),args.legend=list(x=4.8),main="(b)社区堆叠条形图")
mytable2<-table(example2_1$态度,example2_1$性别)
bar3<-barplot(mytable2,xlab="性别",ylab="频数",ylim=c(0,30),col=c("red","green"),legend=rownames(mytable2),args.legend=list(x=4.5),beside=TRUE,main="(c)性别并列条形图")
text(bar3,mytable2,labels=mytable2,pos=3,col=1)
bar4<-barplot(mytable2,xlab="性别",ylab="频数",ylim=c(0,60),col=c("red","green"),legend=rownames(mytable2),args.legend=list(x=1),main="(d)性别堆叠条形图")

条形图及其变种—脊形图

是根据各类别的比例绘制的一种条形图，形状类似脊椎骨，可看做是堆叠条形图的一个变种
绘制脊形图时，将一个类别变量各类别的条的高度都设定为1，条的宽度与观测频数成比例，条内每一段的高度表示另一个类别变量各类别的比例。
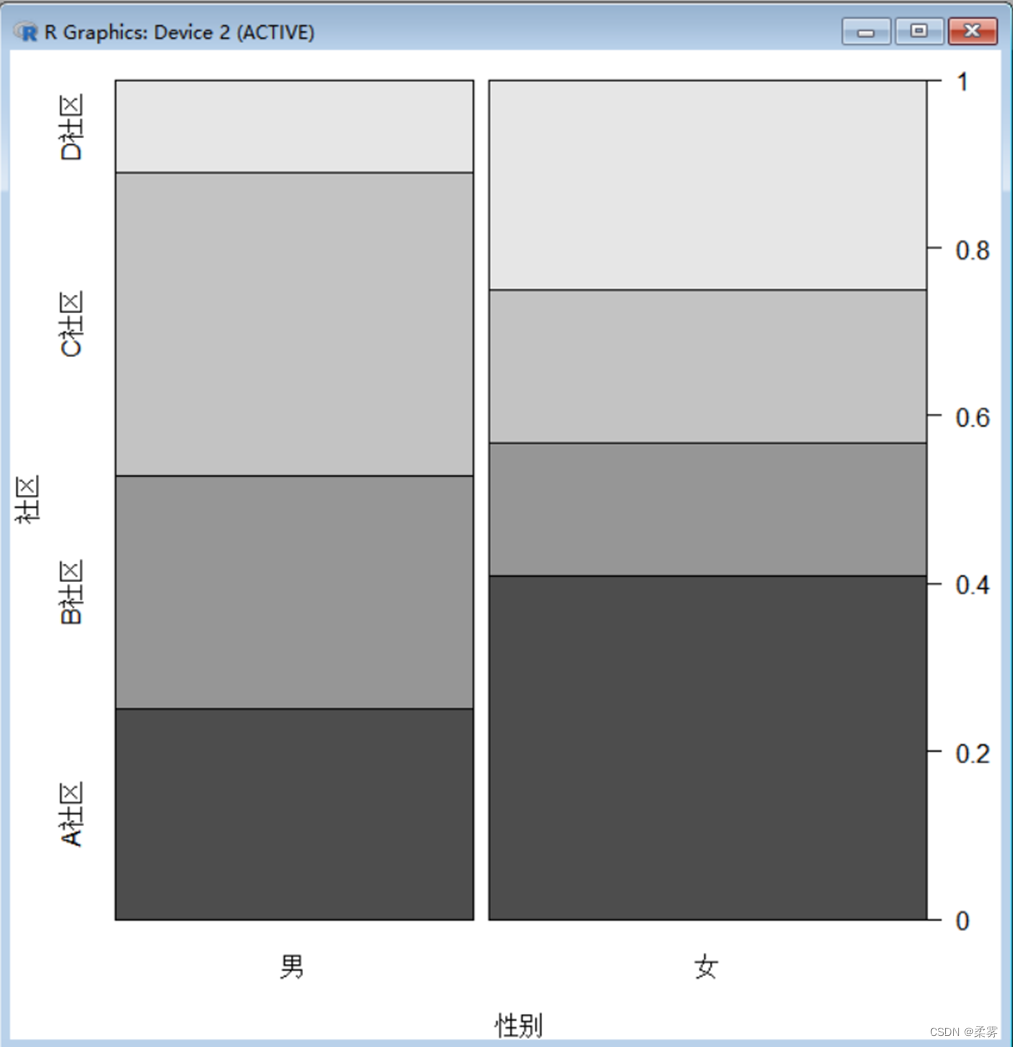
性别与社区的脊形图

load("C:/example/ch2/example2_1.RData")
library(vcd)
spine(社区~性别,data=example2_1,xlab="性别",ylab="社区")

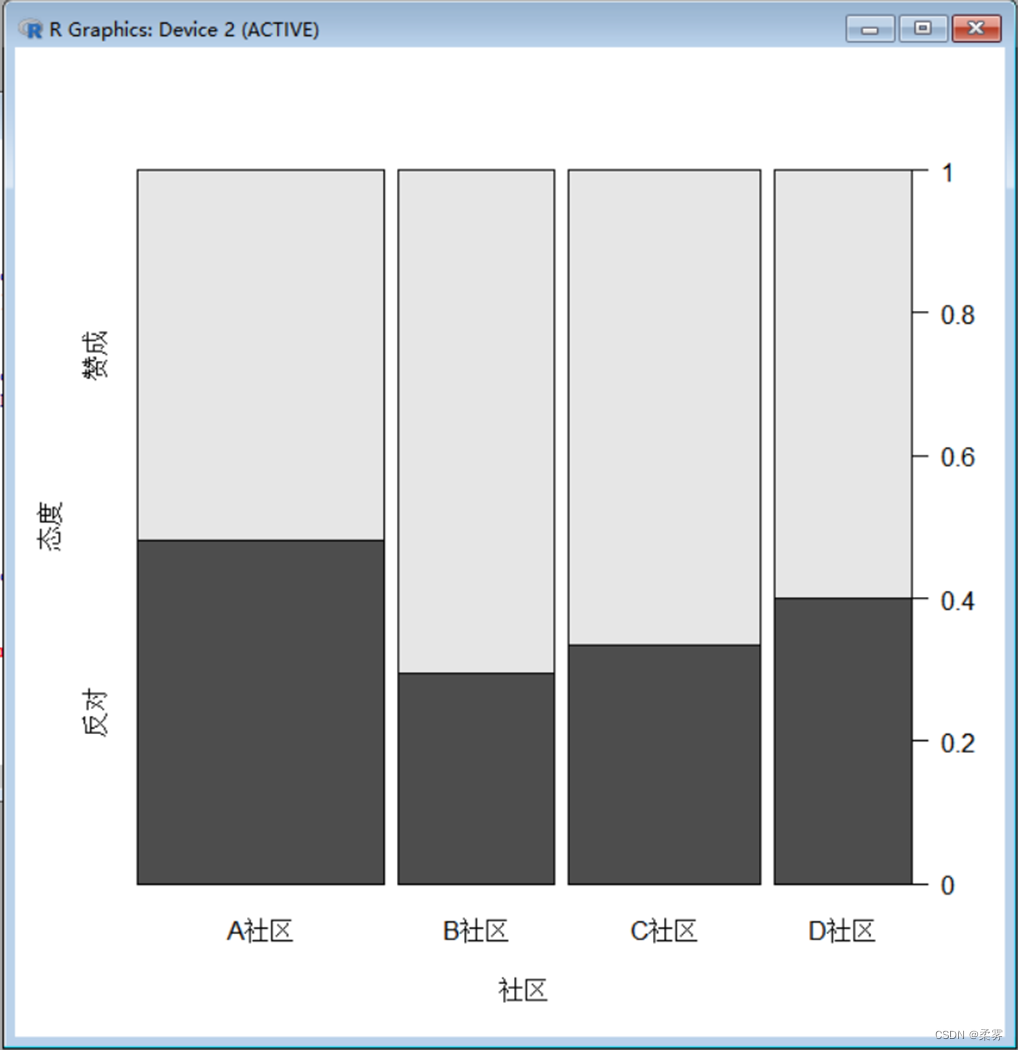
社区与态度的脊形图

spine(态度~社区,data=example2_1,xlab="社区",ylab="态度")

上图，图1反映了被调查者的性别和社区构成。从被调查者的性别构成看，女性条的宽度大于男性条的宽度，表示被调查者中女性的人数比例大于男性。从人数的社区构成看，男性被调查者中D社区所占的比例最小，女性被调查者中A社区所占的比例最大。
上图，图2反映了被调查者的社区和态度构成。不同社区的条的宽度与该社区的人数成比例，每个社区条内的高度反映赞成和反对的人数比例。图显示，从被调查者的社区构成看，A社区的条最宽，D社区的条最窄，表示在全部被调查者中，A社区的人数比例最大，D社区的人数比例最小。从赞成和反对的人数构成看，A社区中表示赞成和反对的比例相当，而在B社区、C社区和D社区中，赞成的比例明显高于反对的比例。

条形图及其变种—马赛克图

马赛克图(mosaicplot)图中的嵌套矩形面积正比于单元格频数。矩形的相对高度和宽度表示不同类别的频数与总频数的比例(更适合展示两个以上的类别变量)
绘马赛克图(mosaicplot)

load("C:/example/ch2/example2_1.RData")
par(mai=c(0.4,0.4,0.2,0.1),cex=.9)
mosaicplot(~性别+社区+态度,data=example2_1,color=2:3,main="")

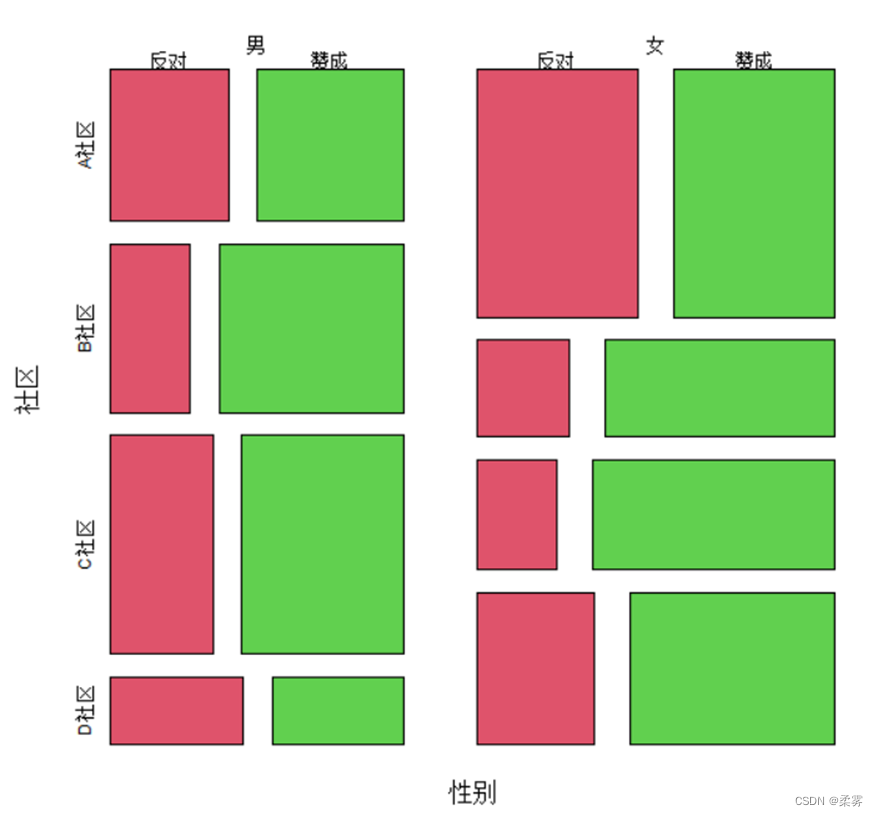
图中矩形的相对高度和宽度取决于相应单元格的频数。这里的矩形长度正比于赞成和反对的比例，而高度则正比于各社区赞成和反对的比例。可以看出，无论是男性还是女性，B社区和C社区赞成的比例都高于反对的比例，而A社区和D社区赞成和反对的比例相差不大。

饼图及其变种—饼图

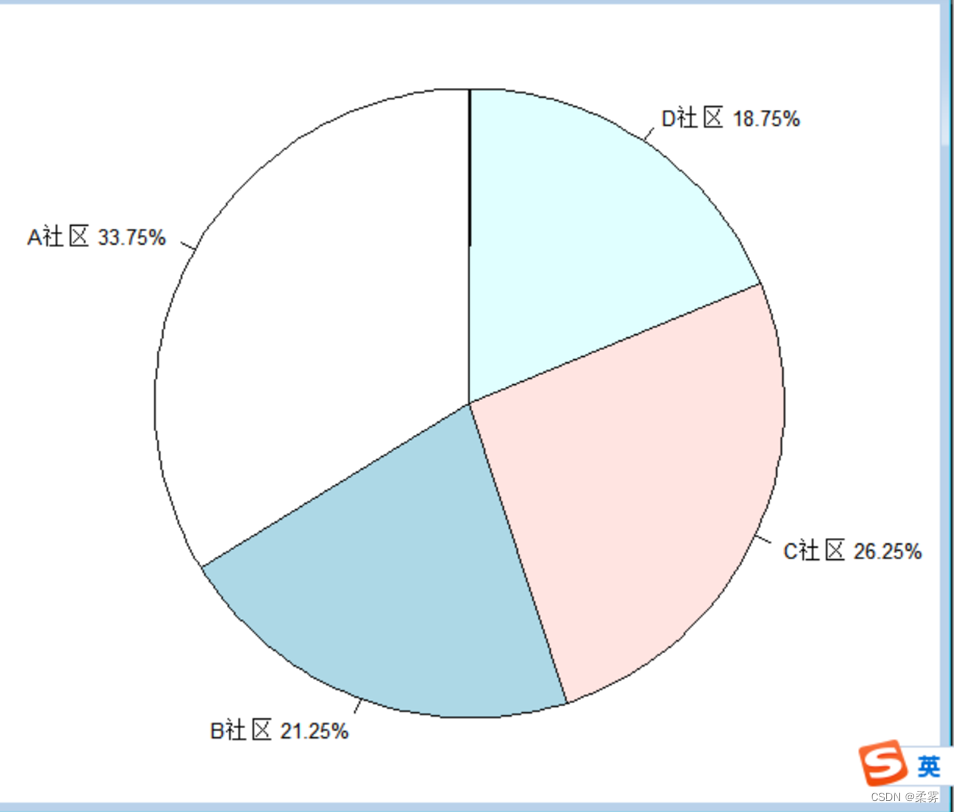
绘制带有百分比的饼图（以不同社区的被调查者人数分布为例）

load("C:/example/ch2/example2_1.RData")
count1<-table(example2_1$社区)
name<-names(count1)
percent<-prop.table(count1)*100
label1<-paste(name," ",percent,"%",sep="")
par(pin=c(3,3),mai=c(0.1,0.4,0.1,0.4),cex=0.8) pie(count1,labels=label1,init.angle=90,radius=1)

绘制3D饼图（以不同社区的被调查者人数分布为例）

load("C:/Users/125/Desktop/example/ch2/example2_1.RData")
library(plotrix)
count1<-table(example2_1$社区)
name<-names(count1)
percent<-prop.table(count1)*100
labs<-paste(name,"",percent,"%",sep="")
pie3D(count1,labels=labs,explode=0.1,labelcex=0.7)#explode每一块的距离，labelcex各分区名称

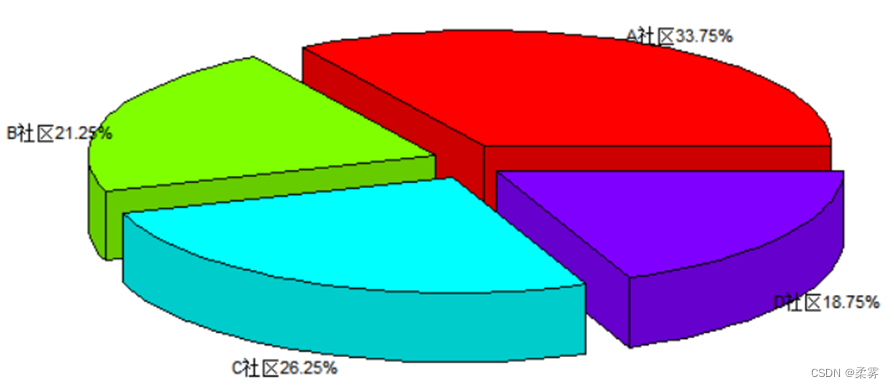
函数pie（x， labels=， radius=，init.agle=，…）创建一个饼图。参数x为一个非负的数值向量。 labels设置饼图各分区的名称。radius=设定半径（默认为0.8）。init. angle=90设定从12点位置开始逆时针方向绘制. paste（，sep=“”）是把若干个R对象链接起来，各对象以sep指定的符号间隔。

饼图及其变种—扇形图

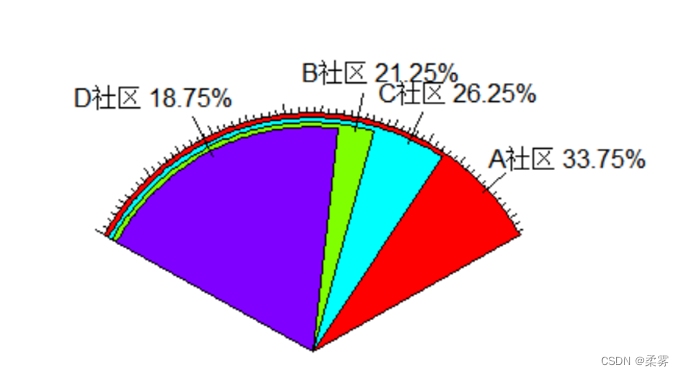
绘制扇形图（以不同社区的被调查者人数分布为例）

load("C:/example/ch2/example2_1.RData")
count1<-table(example2_1$社区)
name<-names(count1)
percent<-count1/sum(count1)*100
labs<-paste(name," ",percent,"%",sep="")
library(plotrix)
fan.plot(count1,labels=labs,ticks=200)

直方图

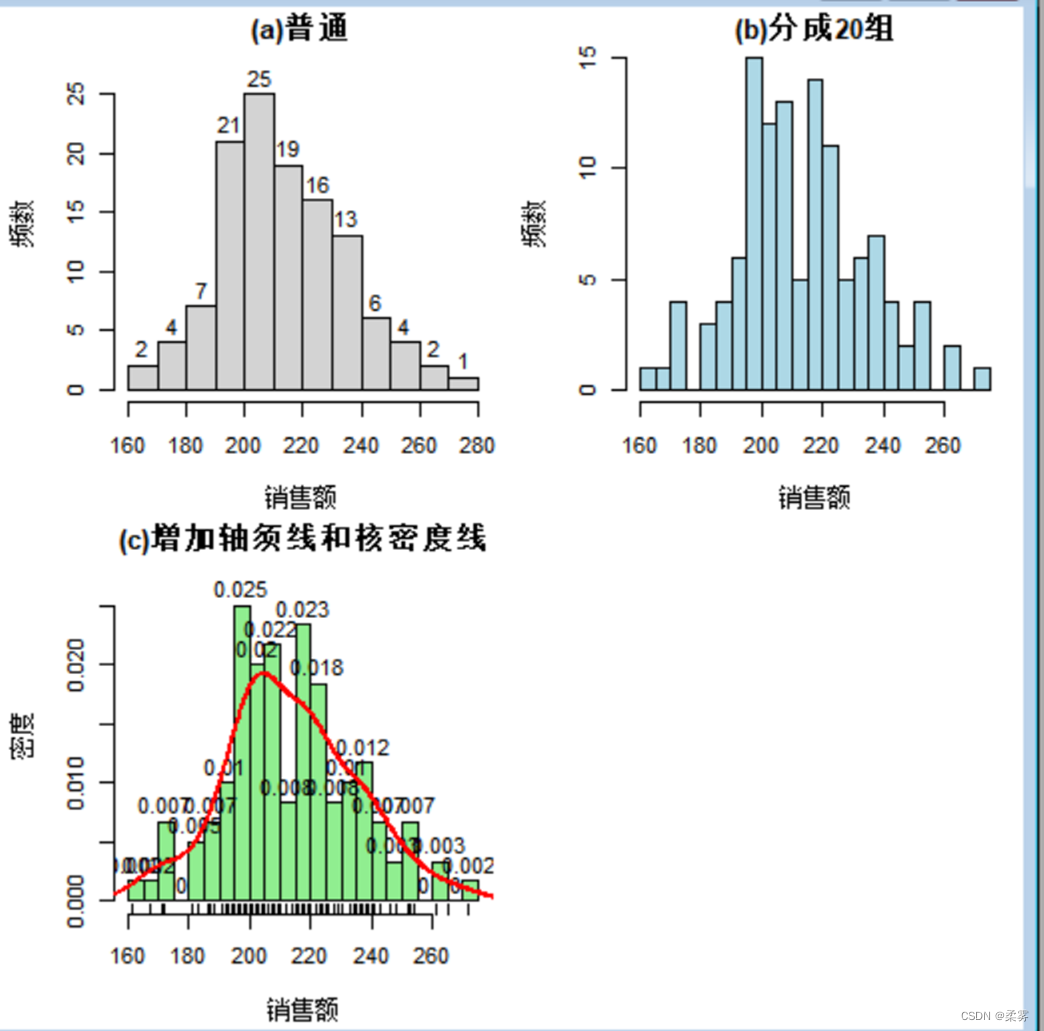
例题2-2：

load("C:/example/ch2/example2_2.RData")
d<-example2_2$销售额
par(mfrow=c(2,2),cex=0.7,mai=c(0.6,0.6,0.2,0.1))
hist(d,ylim=c(0,28),labels=T,xlab ="销售额",ylab="频数",main="(a)普通")
hist(d,breaks=20,col="lightblue",xlab="销售额",ylab="频数",main="(b)分成20组")
hist(d,freq=FALSE,ylim=c(0,0.028),breaks=20,xlab="销售额",ylab="密度",col="lightgreen",labels=T,main="(c)增加轴须线和核密度线")
rug(d)
lines(density(d),col="red",lwd=2)

核密度估计是用于估计随机变量概率密度函数的一种非参数方法。核密度图是估计的概率密度函数的图像。用于观察连续型变量的分布。

茎叶图

load("C:/example/ch2/example2_2.RData")
stem(example2_2$销售额)

library(aplpack)
stem.leaf(example2_2$销售额,1,2)

上图是每个茎列出1次的茎叶图，从中可以看出，销售额主要集中在200万~210万元之间。该茎叶图类似于将数据分成12组后横置的直方图，它所反映的分布特征也与直方图一致。

使用stem.leaf.backback函数绘制背靠背茎叶图（前60天销售额和后60天销售额分别绘制

library(aplpack)
stem.leaf.backback(example2_2$销售额[1:60],example2_2$销售额[61:120])

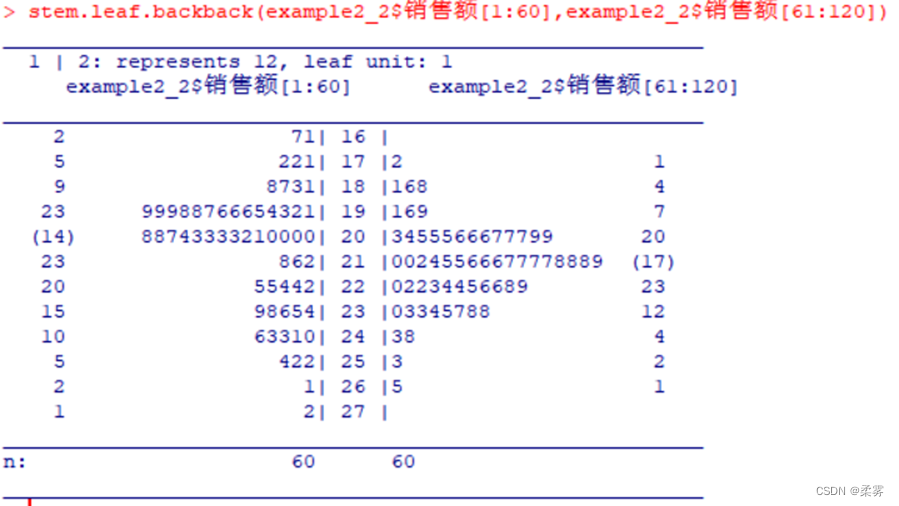
上图是每个茎列出2次的茎叶图，从中可以看出销售额分布的更多细节。图中最左边一列给出的是数据的深度（depth）。什么是数据的深度呢？我们把数据从小到大排序（升序）或从大到小排序（降序），一个数据的深度是指该数据升序和降序中的最小者、比如，194这个数，从小到大排序是第18个，而从大到小排序是第102个，因此该数的深度是18。

茎叶图中每一行列出的是该行中的最大深度。比如，茎为19的那行最大深度出现在数据194，深度为18，因此该行的深度就是18。
在深度那一列中，中位数所在的行用括号括起来，其中的数字5不是指数据深度，而是数据的个数。

箱线图

在2008年8月举行的第29届北京奥运会男子25米手枪速射决赛中，进入决赛的前6名运动员最后20枪的决赛成绩如下表所示。绘制箱线图分析各运动员射击成绩分布的特征。

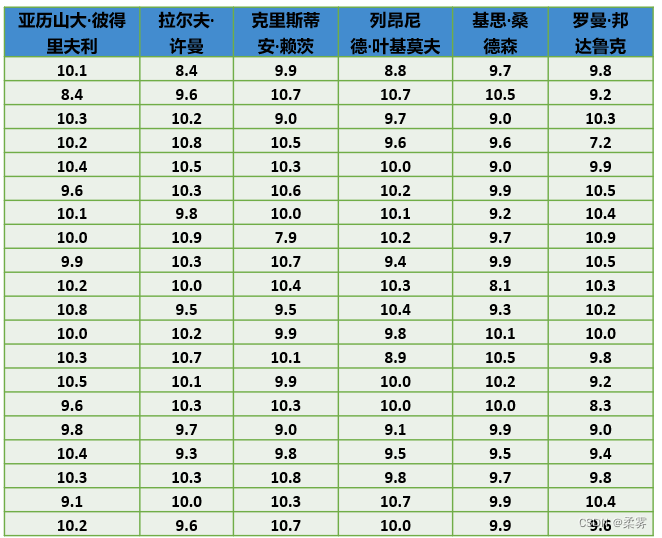
load("C:/example/ch2/example2_3.RData")
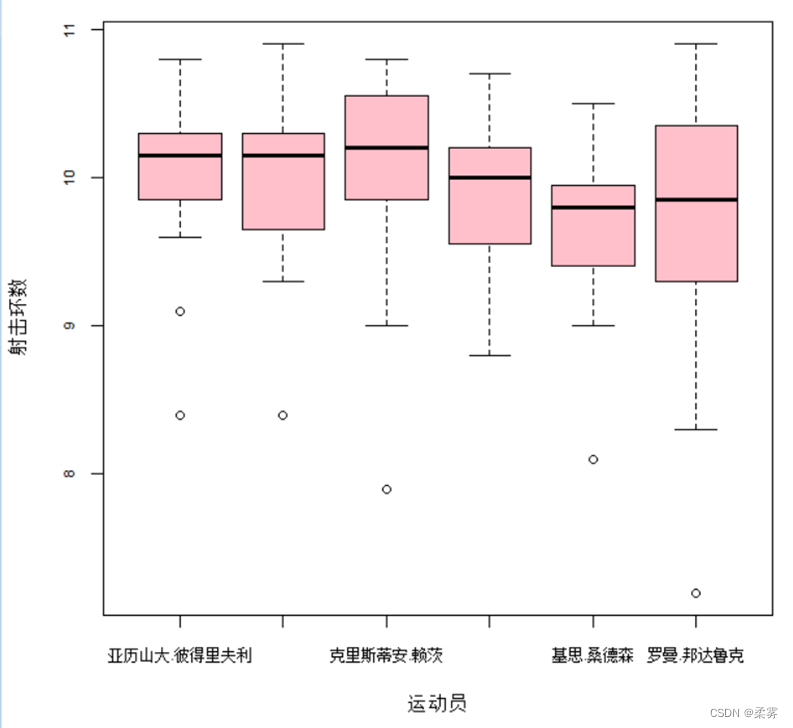
boxplot(example2_3,col="pink",ylab="射击环数",xlab="运动员")

小提琴图

从箱线图不易看出每名运动员射击成绩分布的实际形状。小提琴图（violin plot）作为箱线图的一个变种，将分布的核密度估计曲线与箱线图结合在一起，它在箱线图上以镜像方式叠加一条核密度估计曲线。从核密度估计曲线可以看出数据分布的大致形状。以例2-3的数据为例，绘制小提琴图的R代码和下所示

load("C:/example/ch2/example2_3.RData")
library(vioplot)
par(cex=0.8,mai=c(.7,.7,.1,.1))
x1<-example2_3$亚历山大.彼得里夫利
x2<-example2_3$拉尔夫.许曼
x3<-example2_3$克里斯蒂安.赖茨
x4<-example2_3$列昂尼德.叶基莫夫
x5<-example2_3$基思.桑德森
x6<-example2_3$罗曼.邦达鲁克
vioplot(x1,x2,x3,x4,x5,x6,col="lightblue",names=c("亚历山大.彼得里夫利","拉尔夫.许曼","克里斯蒂安.赖茨","列昂尼德.叶基莫夫","基思.桑德森","罗曼.邦达鲁克"))

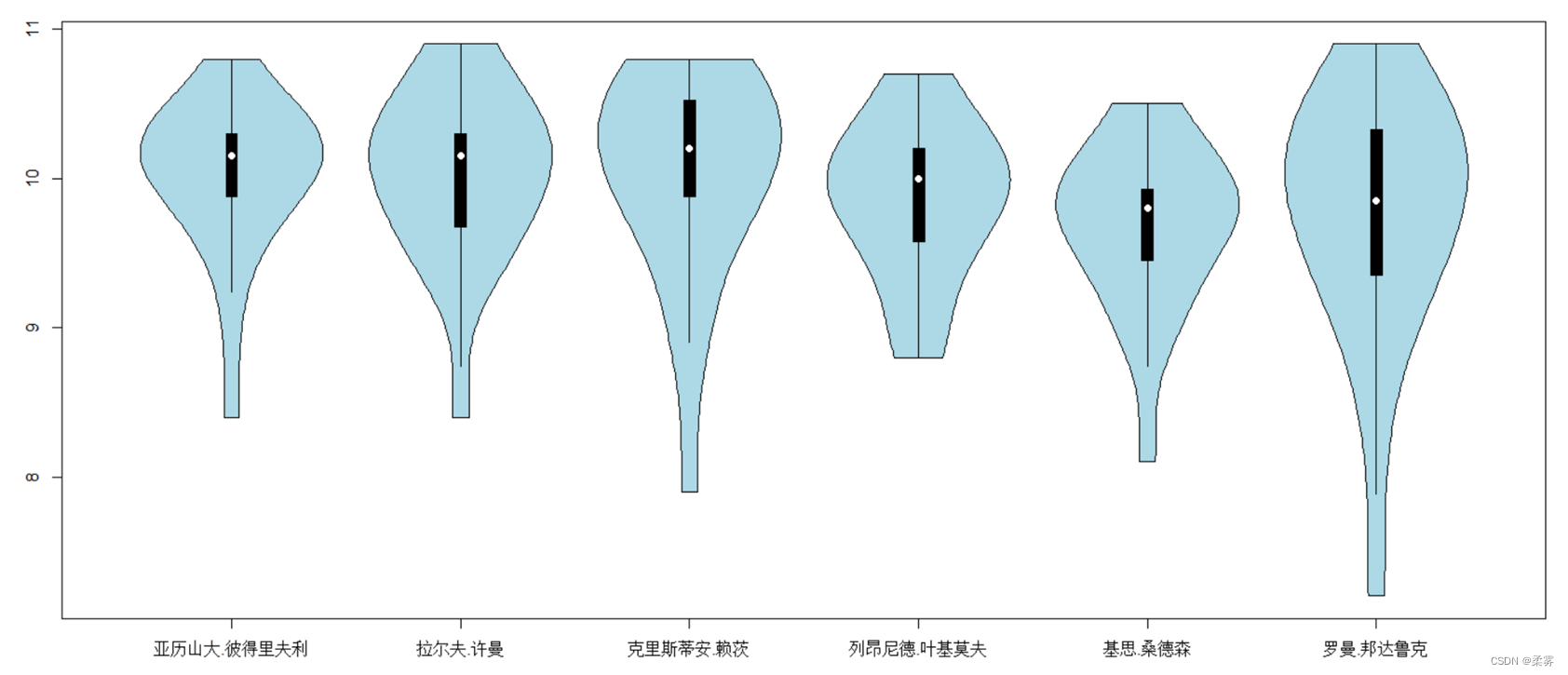
图中白点是中位数，黑色箱子是25%分位数和75%分位数之间的范围。两条黑线为须线。小提琴图显示了比箱线图更多的信息。从图中容易看出每名运动员射击成绩的分布均为左偏分布。

气泡图

对于3个变量之间的关系，可以绘制气泡图(bub-ble plot)，它可以看作散点图的一个变种。其中，第3个变量数值的大小用圆的大小表示。以例2-4中的销售收入、广告费用、销售网点数3个变量为例，绘制气泡图的R代码和结果如下所示：

load("C:/example/ch2/example2_4.RData")
attach(example2_4)
par(mai=c(0.9,0.9,0.1,0.1))
r<- sqrt(销售收入/pi) 
symbols(广告费用,销售网点数, circle=r,inches=0.3,fg="white",bg="lightblue", ylab="销售网点数",xlab="广告费用")
text(广告费用,销售网点数,rownames(example2_4),cex=0.6)
mtext("气泡大小 = 销售收入",line=-2.5,cex=.8,adj=0.1)

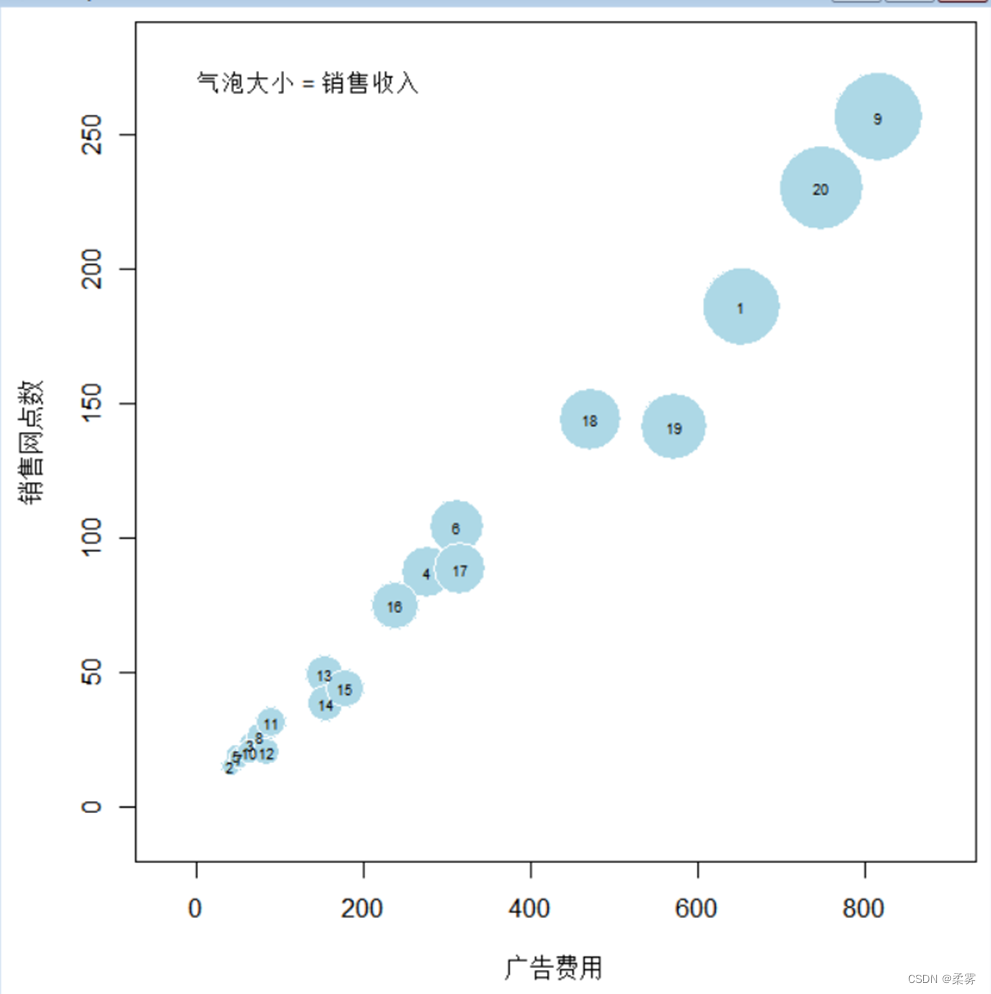
函数symbols(x，y=NULL，circles，inches=TRUE，…)中的x和y为x轴和y轴变量；circles= 第3个变量表示的圆的半径向量；inches=半径英寸；fg=圆的颜色；bg= 圆的填充颜色.text为气泡增加样本标签或编号。

图中的，圆中的数字是样本编号，销售收入越多，圆就越大。可以看出，随着广告费用和销售网点数的增加，销售收入也增加，三者之间均为线性关系。

---

总结

以上就是对数据可视化图形的补充内容，希望对大家的学习有所帮助。