基于时域有限差分法的FDTD的计算电磁学算法-YEE网格下的更新公式推导
基于时域有限差分法的FDTD的计算电磁学算法(含Matlab代码)-YEE网格下的更新公式推导
参考书籍:The finite-difference time-domain method for electromagnetics with MATLAB simulations(国内翻译版本:MATLAB模拟的电磁学时域有限差分法)
代码推荐:The finite-difference time-domain method for electromagnetics with MATLAB simulations的附件代码
我最初也是基于这个代码学习的
FDTD算法:采用差分直接离散时域Maxwell方程,电磁场的求解基于时间步的迭代,无需存储全空间的电磁场信息,内存消耗较小,同时采用立方体网格和差分算法,网格形式和算法均十分简单,计算速度快,基于时域算法,特别适合“宽带问题”的求解。但是,简单的立方体方体网格带来的弊端就是模型拟合精度较低,对于含有精细结构的模型,计算精度较低,同时基于“微分方程”,计算区域需要设置截断。
详细对比参考:常用计算电磁学算法特性与电磁软件分析
1、从麦克斯韦开始的FDTD时域有限差分法
1.1 麦克斯韦方程
FDTD叫时域有限差分法,显然,其依赖的麦克斯韦方程也是时域的。麦克斯韦时域微分方程为:
?
×
H
=
?
D
?
t
+
J
?
×
E
=
?
?
B
?
t
?
M
?
?
D
=
ρ
e
?
?
B
=
ρ
m
\begin{gathered} \nabla\times \mathbf{H}= {\frac{\partial \mathbf{D}}{\partial t}}+\boldsymbol{J} \\ \nabla\times \mathbf{E}=-{\frac{\partial \mathbf{B}}{\partial t}}-\mathbf{M} \\ \nabla\cdot\mathbf{D}=\rho_{\mathrm{e}} \\ \nabla\cdot \mathbf{B}=\rho_{m} \end{gathered}
?×H=?t?D?+J?×E=??t?B??M??D=ρe???B=ρm??
式中,E为电场强度(V/m);D为电位移(C/m);H为磁场强度(A/m);B为磁通量密度(Wb/m°);J为电流密度(A/m);M为磁流密度(V/m);
ρ
e
\rho_{e}
ρe?为电荷密度(C/m);
ρ
m
\rho_{m}
ρm?为磁荷密度(Wb/m)。
依稀记得当时老师说,麦克斯韦方程有其直观理解,分别是:
1. 变化的电场和电流会产生磁场
2. 变化的磁场和磁荷会产生电场(自然界无磁荷,一般是等效出来)
3. 电流源产生电场
4. 磁流源产生磁场
1.2 本构关系
本构关系对补充麦克斯韦方程和描述媒质的特性是必要的,本构关系对线性、各向同性和非色散媒质可以写成:
D
=
ε
E
B
=
μ
H
.
\begin{aligned}D&=\varepsilon E\\B&=\mu H\end{aligned}.
DB?=εE=μH?.
其中,
ε
\varepsilon
ε为媒质的介电常数;
μ
\mu
μ为媒质的磁导率。在自由空间,有:
ε
=
ε
0
=
8.854
×
1
0
?
12
F
/
m
μ
=
μ
0
=
4
π
×
1
0
?
7
H
/
m
\begin{aligned}\varepsilon=&\varepsilon_0=8.854\times10^{-12}\quad\mathrm{F/m}\\\mu=&\mu_0=4\pi\times10^{-7}\quad\mathrm{H/m}\end{aligned}
ε=μ=?ε0?=8.854×10?12F/mμ0?=4π×10?7H/m?
在常规的电磁学表述中,我们更多的使用相对介电常数。比如说耳熟能详的FR4板材,其相对介电常数大概是
ε
r
=
4.2
\varepsilon_r=4.2
εr?=4.2。 这就代表其实际的介电常数为
ε
F
R
4
=
ε
r
ε
0
\varepsilon_{FR4}=\varepsilon_r\varepsilon_0
εFR4?=εr?ε0?。但是,还有一个重要参数和本构关系相关,那就是损耗角正切
t
a
n
δ
tan \delta
tanδ。
对于FR4板材,一般认为其损耗角正切为
t
a
n
δ
=
0.02
tan \delta=0.02
tanδ=0.02,根据微波工程1.3小节的公式:
?
=
?
′
?
j
?
′
′
=
?
′
(
1
?
j
tan
?
δ
)
=
?
0
?
r
(
1
?
j
tan
?
δ
)
\epsilon=\epsilon^{\prime}-j\epsilon^{\prime\prime}=\epsilon^{\prime}(1-j\tan\delta)=\epsilon_{0}\epsilon_{r}(1-j\tan\delta)
?=?′?j?′′=?′(1?jtanδ)=?0??r?(1?jtanδ),其对应的介电常数应该是:
ε
F
R
4
=
ε
r
(
1
?
j
tan
?
δ
)
ε
0
=
(
4.2
?
j
0.02
)
ε
0
\varepsilon_{FR4}=\varepsilon_r(1-j\tan\delta)\varepsilon_0=(4.2-j0.02)\varepsilon_0
εFR4?=εr?(1?jtanδ)ε0?=(4.2?j0.02)ε0?
其对应的相对介电常数为:4.2-j0.02
在进行FDTD的推导时,因为在 FDTD 的更新方程的过程中满足散度方程,所以只需要考虑两个旋度方程即可。麦克斯韦中的电流密度
J
\boldsymbol{J}
J等于导体电流密度
J
c
\boldsymbol{J_c}
Jc?与施加电流密度
J
i
\boldsymbol{J_i}
Ji?之和,即:
J
=
J
c
+
J
i
\boldsymbol{J}=\boldsymbol{J_{\mathrm{c}}}+\boldsymbol{J_{\mathrm{i}}}
J=Jc?+Ji?
对于磁流密度,也类似:
M
=
M
c
+
M
i
\boldsymbol{M}=\boldsymbol{M_{\mathrm{c}}}+\boldsymbol{M_{\mathrm{i}}}
M=Mc?+Mi?
因此,对原来的麦克斯韦方程拆分一下,就是:
?
×
H
=
ε
?
E
?
t
+
σ
e
E
+
J
i
\nabla\times \boldsymbol{H}=\varepsilon\frac{\partial \boldsymbol{E}}{\partial t}+\sigma^{e}\boldsymbol{E}+\boldsymbol{J_{i}}
?×H=ε?t?E?+σeE+Ji?
和:
?
×
E
=
?
μ
?
H
?
t
?
σ
m
H
?
M
i
\nabla\times \boldsymbol{E}=-\mu\frac{\partial \boldsymbol{H}}{\partial t}-\sigma^{m}\boldsymbol{H}-\boldsymbol{M_{i}}
?×E=?μ?t?H??σmH?Mi?
旋度的计算公式大家还记得不:
?
×
F
(
x
,
y
,
z
)
=
∣
i
^
j
^
k
^
?
?
x
?
?
y
?
?
z
F
x
F
y
F
z
∣
=
(
?
F
z
?
y
?
?
F
y
?
z
)
i
^
+
(
?
F
x
?
z
?
?
F
z
?
x
)
j
^
+
(
?
F
y
?
x
?
?
F
x
?
y
)
k
^
\begin{aligned} &\nabla\times\mathbf{F}(x,y,z)=\begin{vmatrix}\hat{\boldsymbol{i}}&\hat{\boldsymbol{j}}&\hat{\boldsymbol{k}}\\\frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\F_x&F_y&F_z\end{vmatrix} \\ &=\left(\frac{\partial F_z}{\partial y}-\frac{\partial F_y}{\partial z}\right)\hat{\boldsymbol{i}}+\left(\frac{\partial F_x}{\partial z}-\frac{\partial F_z}{\partial x}\right)\hat{\boldsymbol{j}}+\left(\frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y}\right)\hat{\boldsymbol{k}} \end{aligned}
??×F(x,y,z)=
?i^?x??Fx??j^??y??Fy??k^?z??Fz??
?=(?y?Fz????z?Fy??)i^+(?z?Fx????x?Fz??)j^?+(?x?Fy????y?Fx??)k^?
把麦克斯韦旋度方程按照三个方向x,y,z全部展开,就可以得到6个方程:
?
E
x
?
t
=
1
ε
x
(
?
H
z
?
y
?
?
H
y
?
z
?
σ
x
e
E
x
?
J
i
x
)
?
E
y
?
t
=
1
ε
y
(
?
H
x
?
z
?
?
H
z
?
x
?
σ
y
e
E
y
?
J
i
y
)
?
E
z
?
t
=
1
ε
z
(
?
H
y
?
x
?
?
H
x
?
y
?
σ
z
e
E
z
?
J
i
z
)
?
H
x
?
t
=
1
μ
x
(
?
E
y
?
z
?
?
E
z
?
y
?
σ
x
m
H
x
?
M
i
x
)
?
H
y
?
t
=
1
μ
y
(
?
E
x
?
x
?
?
E
x
?
z
?
σ
y
m
H
y
?
M
i
y
)
?
H
z
?
t
=
1
μ
z
(
?
E
x
?
y
?
?
E
y
?
x
?
σ
z
m
H
z
?
M
i
z
)
\begin{gathered} \frac{\partial\boldsymbol{E}_x}{\partial t}= \frac1{\varepsilon_x}\Big(\frac{\partial H_z}{\partial y}-\frac{\partial H_y}{\partial z}-\sigma_x^eE_x-J_{ix}\Big) \\ \frac{\partial E_y}{\partial t}= \frac1{\varepsilon_y}\Big(\frac{\partial H_x}{\partial z}-\frac{\partial H_z}{\partial x}-\sigma_y^eE_y-J_{iy}\Big) \\ \frac{\partial E_z}{\partial t}= \frac{1}{\varepsilon_{z}}\Big(\frac{\partial H_{y}}{\partial x}-\frac{\partial H_{x}}{\partial y}-\sigma_{z}^{e}E_{z}-J_{iz}\Big) \\ \frac{\partial H_x}{\partial t}= \frac1{\mu_x}\Big(\frac{\partial E_y}{\partial z}-\frac{\partial E_z}{\partial y}-\sigma_x^mH_x-M_{ix}\Big) \\ \frac{\partial H_y}{\partial t}= \frac1{\mu_y}\Big(\frac{\partial\boldsymbol{E}_x}{\partial x}-\frac{\partial\boldsymbol{E}_x}{\partial\boldsymbol{z}}-\boldsymbol{\sigma}_y^\mathfrak{m}H_y-\boldsymbol{M}_{iy}\Big) \\ \frac{\partial H_z}{\partial t}= \frac{1}{\mu_{z}}\Big(\frac{\partial\boldsymbol{E}_{x}}{\partial y}-\frac{\partial\boldsymbol{E}_{y}}{\partial x}-\sigma_{z}^{\mathfrak{m}}H_{z}-\boldsymbol{M}_{iz}\Big) \end{gathered}
?t?Ex??=εx?1?(?y?Hz????z?Hy???σxe?Ex??Jix?)?t?Ey??=εy?1?(?z?Hx????x?Hz???σye?Ey??Jiy?)?t?Ez??=εz?1?(?x?Hy????y?Hx???σze?Ez??Jiz?)?t?Hx??=μx?1?(?z?Ey????y?Ez???σxm?Hx??Mix?)?t?Hy??=μy?1?(?x?Ex????z?Ex???σym?Hy??Miy?)?t?Hz??=μz?1?(?y?Ex????x?Ey???σzm?Hz??Miz?)?
2、空间差分与时间差分
2.1、非常简单的差分方程
FDTD是在离散网格中进行迭代的,上面的麦克斯韦公式有大量的求导计算,这该如何解决呢?答案是差分近似。大家学高数都学过导数的近似吧:
f
′
(
x
)
=
lim
?
Δ
x
→
0
f
(
x
+
Δ
x
)
?
f
(
x
)
Δ
x
f^{'}(x)=\underset{\Delta x\to0}{\operatorname*{lim}}\frac{f(x+\Delta x)-f(x)}{\Delta x}
f′(x)=Δx→0lim?Δxf(x+Δx)?f(x)?
如果
Δ
x
\Delta x
Δx非常小,那么:
f
′
(
x
)
≈
f
(
x
+
Δ
x
)
?
f
(
x
)
Δ
x
f^{'}(x)\approx\frac{f(x+\Delta x)-f(x)}{\Delta x}
f′(x)≈Δxf(x+Δx)?f(x)?
但是为了实现更高的精度,所以采用FDTD都会采用双向差分公式:
f
′
(
x
)
≈
f
(
x
+
Δ
x
)
?
f
(
x
?
Δ
x
)
2
Δ
x
f^{^{\prime}}(x){\approx}\frac{f(x+\Delta x)-f(x-\Delta x)}{2\Delta x}
f′(x)≈2Δxf(x+Δx)?f(x?Δx)?
实际上,此处使用的是近似,也存在高阶的FDTD的算法,对于此近似考虑了更多项,精度会更高(参考“基于高阶时域有限差分法平面波及完全匹配层的研究”等):
f
′
(
x
)
=
f
(
x
+
Δ
x
)
?
f
(
x
?
Δ
x
)
2
Δ
x
?
(
Δ
x
2
)
6
+
.
.
.
=
f
(
x
+
Δ
x
)
?
f
(
x
?
Δ
x
)
2
Δ
x
+
O
(
(
Δ
x
)
2
)
f^{\prime}(x)=\frac{f(x+\Delta x)-f(x-\Delta x)}{2\Delta x}-\frac{(\Delta x^{2})}{6}+...=\frac{f(x+\Delta x)-f(x-\Delta x)}{2\Delta x}+O((\Delta x)^{2})
f′(x)=2Δxf(x+Δx)?f(x?Δx)??6(Δx2)?+...=2Δxf(x+Δx)?f(x?Δx)?+O((Δx)2)
2.2、差分方程的运用
在FDTD算法中,网格被剖分为YEE网格的形式,电场和磁场元胞差半个身位,其更新的时间步也是差
0.5
Δ
t
0.5\Delta t
0.5Δt:
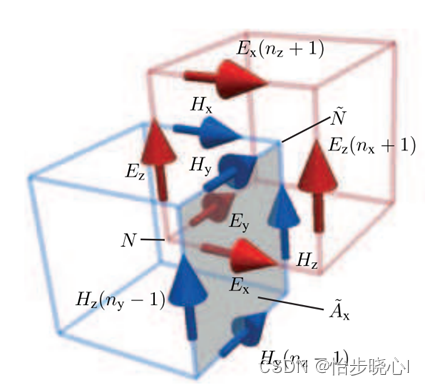
具体来讲,实际的电场网格和磁场网格的位置是:
E
x
(
i
,
j
,
k
)
?
(
(
i
?
0
,
5
)
Δ
x
,
(
j
?
1
)
Δ
y
,
(
k
?
1
)
Δ
z
)
E
y
(
i
,
j
,
k
)
?
(
(
i
?
1
)
Δ
x
,
(
j
?
0.5
)
Δ
y
,
(
k
?
1
)
Δ
z
)
E
z
(
i
,
j
,
k
)
?
(
(
i
?
1
)
Δ
x
,
(
j
?
1
)
Δ
y
,
(
k
?
0.5
)
Δ
z
)
H
x
(
i
,
j
,
k
)
?
(
(
i
?
1
)
Δ
x
,
(
j
?
0.5
)
Δ
y
,
(
k
?
0.5
)
Δ
z
)
H
y
(
i
,
j
,
k
)
?
(
(
i
?
0.5
)
Δ
x
,
(
j
?
1
)
Δ
y
,
(
k
?
0.5
)
Δ
z
)
H
z
(
i
,
j
,
k
)
?
(
(
i
?
0.5
)
Δ
x
,
(
j
?
0.5
)
Δ
y
,
(
k
?
1
)
Δ
z
)
\begin{aligned} E_x(i,j,k)\Rightarrow\left((i-0,5)\Delta x,(j-1)\Delta y,(k-1)\Delta z\right)\\ E_y(i,j,k)\Rightarrow\left((i-1)\Delta x,(j-0.5)\Delta y,(k-1)\Delta z\right)\\ E_z(i,j,k)\Rightarrow\left((i-1)\Delta x,(j-1)\Delta y,(k-0.5)\Delta z\right)\\ H_x(i,j,k)\Rightarrow\left((i-1)\Delta x,(j-0.5)\Delta y,(k-0.5)\Delta z\right)\\ H_y(i,j,k)\Rightarrow((i-0.5)\Delta x,(j-1)\Delta y,(k-0.5)\Delta z) \\ H_z(i,j,k)\Rightarrow((i-0.5)\Delta x,(j-0.5)\Delta y,(k-1)\Delta z) \end{aligned}
Ex?(i,j,k)?((i?0,5)Δx,(j?1)Δy,(k?1)Δz)Ey?(i,j,k)?((i?1)Δx,(j?0.5)Δy,(k?1)Δz)Ez?(i,j,k)?((i?1)Δx,(j?1)Δy,(k?0.5)Δz)Hx?(i,j,k)?((i?1)Δx,(j?0.5)Δy,(k?0.5)Δz)Hy?(i,j,k)?((i?0.5)Δx,(j?1)Δy,(k?0.5)Δz)Hz?(i,j,k)?((i?0.5)Δx,(j?0.5)Δy,(k?1)Δz)?
更新的时间步也是差 0.5 Δ t 0.5\Delta t 0.5Δt:FDTD算法在离散的时间瞬间取样和计算场值,但是电场和磁场取样计算并不是在相同的时刻。对时间步 Δ t \Delta t Δt,电场E的取样时刻为:0, Δ t \Delta t Δt,2 Δ t \Delta t Δt,3 Δ t \Delta t Δt,…,n Δ t \Delta t Δt;而磁场H取样时刻为:0.5 Δ t \Delta t Δt,1.5 Δ t \Delta t Δt,2.5 Δ t \Delta t Δt,…(n+0.5) Δ t \Delta t Δt。即电场取样在时间的整数步长时刻,而磁场取样时刻为半整数时间步时刻。它们之间的时间差为半个时间步。
因此,考虑一个上面得到的麦克斯韦的方程(以Ex方向为例):
?
E
x
?
t
=
1
ε
x
(
?
H
z
?
y
?
?
H
y
?
z
?
σ
x
e
E
x
?
J
i
r
)
\frac{\partial E_x}{\partial t}=\frac1{\varepsilon_x}\left(\frac{\partial H_z}{\partial y}-\frac{\partial H_y}{\partial z}-\sigma_x^eE_x-J_{ir}\right)
?t?Ex??=εx?1?(?y?Hz????z?Hy???σxe?Ex??Jir?)
观察其导数项,分别有时间的差分项
?
E
x
?
t
\frac{\partial E_x}{\partial t}
?t?Ex??和空间的差分项
?
H
z
?
y
\frac{\partial H_z}{\partial y}
?y?Hz??和
?
H
y
?
z
\frac{\partial H_y}{\partial z}
?z?Hy??。
方程中的导数可以用中心差分来近似,此时
E
x
n
(
i
,
j
,
k
)
E_x^n(i,j,k)
Exn?(i,j,k)的位置为中心差分公式的中心点,而时间上应以
(
n
+
0.5
)
Δ
t
(n+0.5)\Delta t
(n+0.5)Δt作为中心点(因为电场E的取样时刻为:0,
Δ
t
\Delta t
Δt,2
Δ
t
\Delta t
Δt,3
Δ
t
\Delta t
Δt,…,n
Δ
t
\Delta t
Δt,而
(
n
+
0.5
)
Δ
t
(n+0.5)\Delta t
(n+0.5)Δt差分后可以得到n和n+1,符合取样时刻)。因此,第一项
?
E
x
?
t
\frac{\partial E_x}{\partial t}
?t?Ex??可以写成如下的差分形式:
E
x
n
+
0.5
(
i
,
j
,
k
)
=
E
x
n
+
1
(
i
,
j
,
k
)
?
E
x
n
(
i
,
j
,
k
)
Δ
t
E_x^{n+0.5}(i,j,k)=\frac{E_x^{n+1}(i,j,k)-E_x^n(i,j,k)}{\Delta t}
Exn+0.5?(i,j,k)=ΔtExn+1?(i,j,k)?Exn?(i,j,k)?
而空间的差分项
?
H
z
?
y
\frac{\partial H_z}{\partial y}
?y?Hz??可以写成:
?
H
z
?
y
=
H
z
n
+
1
2
(
i
,
j
,
k
)
?
H
z
n
+
1
2
(
i
,
j
?
1
,
k
)
Δ
y
\frac{\partial H_z}{\partial y}=\frac{H_z^{n+\frac12}(i,j,k)-H_z^{n+\frac12}(i,j-1,k)}{\Delta y}
?y?Hz??=ΔyHzn+21??(i,j,k)?Hzn+21??(i,j?1,k)?
2.3、得到差分方程
把所有项都写成差分形式,就可以得到3D的FDTD更新方程:
E
x
n
+
1
(
i
,
j
,
k
)
=
C
e
x
e
(
i
,
j
,
k
)
×
E
x
n
(
i
,
j
,
k
)
+
C
e
x
h
z
(
i
,
j
,
k
)
×
(
H
z
n
+
1
2
(
i
,
j
,
k
)
?
H
z
n
+
1
2
(
i
,
j
?
1
,
k
)
)
+
C
e
x
h
y
(
i
,
j
,
k
)
×
(
H
y
n
+
1
2
(
i
,
j
,
k
)
?
H
y
n
+
1
2
(
i
,
j
,
k
?
1
)
)
+
C
e
x
j
(
i
,
j
,
k
)
×
J
i
x
n
+
1
2
(
i
,
j
,
k
)
\begin{aligned} E_{x}^{n+1}\left(i,j,k\right)& =C_{exe}(i,j,k)\times E_x^n(i,j,k) \\ &+C_{exhz}(i,j,k)\times(H_{z}^{n+\frac12}(i,j,k)-H_{z}^{n+\frac12}(i,j-1,k)) \\ &+C_{\mathrm{exhy}}(i,j,k)\times(H_y^{n+\frac12}(i,j,k)-H_y^{n+\frac12}(i,j,k-1)) \\ &+C_{exj}\left(i,j,k\right)\times J_{ix}^{n+\frac12}(i,j,k) \end{aligned}
Exn+1?(i,j,k)?=Cexe?(i,j,k)×Exn?(i,j,k)+Cexhz?(i,j,k)×(Hzn+21??(i,j,k)?Hzn+21??(i,j?1,k))+Cexhy?(i,j,k)×(Hyn+21??(i,j,k)?Hyn+21??(i,j,k?1))+Cexj?(i,j,k)×Jixn+21??(i,j,k)?
C开头的都是系数,为了书写方便,其实际的值为:
C
e
x
e
(
i
,
j
,
k
)
=
2
ε
z
(
i
,
j
,
k
)
?
Δ
t
σ
z
e
(
i
,
j
,
k
)
2
ε
z
(
i
,
j
,
k
)
+
Δ
t
σ
z
e
(
i
,
j
,
k
)
C
e
x
h
y
(
i
,
j
,
k
)
=
2
Δ
t
(
2
ε
z
(
i
,
j
,
k
)
+
Δ
t
σ
z
e
(
i
,
j
,
k
)
)
Δ
x
C
e
x
h
y
(
i
,
j
,
k
)
=
?
2
Δ
t
(
2
ε
z
(
i
,
j
,
k
)
+
Δ
t
σ
z
e
(
i
,
j
,
k
)
)
Δ
y
C
e
x
j
(
i
,
j
,
k
)
=
?
2
Δ
t
2
ε
z
(
i
,
j
,
k
)
+
Δ
t
σ
z
e
(
i
,
j
,
k
)
\begin{gathered} C_{exe}(i,j,k)= \frac{2\varepsilon_z(i,j,k)-\Delta t\sigma_z^e(i,j,k)}{2\varepsilon_z(i,j,k)+\Delta t\sigma_z^e(i,j,k)} \\ C_{exhy}(i,j,k)= \frac{2\Delta t}{(2\varepsilon_z(i,j,k)+\Delta t\sigma_z^e(i,j,k))\Delta x} \\ C_{{exhy}}(i,j,k)= -\frac{2\Delta t}{(2\varepsilon_z(i,j,k)+\Delta t\sigma_z^e(i,j,k))\Delta y} \\ C_{exj}\left(i,j,k\right) =-\frac{2\Delta t}{2\varepsilon_z(i,j,k)+\Delta t\sigma_z^e(i,j,k)} \end{gathered}
Cexe?(i,j,k)=2εz?(i,j,k)+Δtσze?(i,j,k)2εz?(i,j,k)?Δtσze?(i,j,k)?Cexhy?(i,j,k)=(2εz?(i,j,k)+Δtσze?(i,j,k))Δx2Δt?Cexhy?(i,j,k)=?(2εz?(i,j,k)+Δtσze?(i,j,k))Δy2Δt?Cexj?(i,j,k)=?2εz?(i,j,k)+Δtσze?(i,j,k)2Δt??
当然,这只是6个方程中的一个,更加详细的方程参考:
MATLAB模拟的电磁学时域有限差分法的1.3。看看对应的matlab代码是怎么写的(没有电流就可以省略Cexj):
current_time = current_time + dt/2;
Ex(1:nx,2:ny,2:nz) = Cexe(1:nx,2:ny,2:nz).*Ex(1:nx,2:ny,2:nz) ...
+ Cexhz(1:nx,2:ny,2:nz).*...
(Hz(1:nx,2:ny,2:nz)-Hz(1:nx,1:ny-1,2:nz)) ...
+ Cexhy(1:nx,2:ny,2:nz).*...
(Hy(1:nx,2:ny,2:nz)-Hy(1:nx,2:ny,1:nz-1));
% General electric field updating coefficients
% Coeffiecients updating Ex
Cexe = (2*eps_r_x*eps_0 - dt*sigma_e_x) ...
./(2*eps_r_x*eps_0 + dt*sigma_e_x);
Cexhz = (2*dt/dy)./(2*eps_r_x*eps_0 + dt*sigma_e_x);
Cexhy = -(2*dt/dz)./(2*eps_r_x*eps_0 + dt*sigma_e_x);
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!