【MATLAB】数据拟合第12期-基于高斯核回归的拟合算法
有意向获取代码,请转文末观看代码获取方式~也可转原文链接获取~

1 基本定义
基于高斯核回归的拟合算法是一种处理回归问题的机器学习方法。以下是该算法的简单介绍:
-
核心思想:高斯核回归的核心思想是利用高斯核函数对数据点进行非线性映射,将数据从原始空间映射到一个高维特征空间。
-
优势:通过引入高斯核函数,可以将原始数据从低维空间映射到高维空间,从而捕捉更多的特征信息。这种非线性映射的方式使得高斯回归在处理复杂的非线性关系时表现出更好的性能。
-
拟合过程:在高维空间中,通过最小化损失函数来拟合数据点的概率分布,从而得到回归模型。
总的来说,基于高斯核回归的拟合算法通过非线性映射和最小化损失函数来实现对数据的拟合,对于处理复杂的非线性关系问题有较好的效果。
基于高斯核回归的拟合算法具有以下优点:
-
具有平滑性质,能够拟合非线性数据。
-
天然支持得到模型关于预测的不确定性(置信区间),直接输出关于预测点值的概率分布。
-
通过最大化边缘似然这一简洁的方式,可以在不需要交叉验证的情况下给出比较好的正则化效果。
然而,基于高斯核回归的拟合算法也存在一些缺点:
-
计算复杂度高:随着数据量的增加,计算复杂度也相应增加,需要大量的计算资源。
-
对数据采样要求高:需要大量的数据采样才能准确地估计函数的形状,因此对数据采样的要求比较高。
-
参数选择困难:需要选择合适的核函数和超参数,这需要大量的经验和调试。
基于高斯核回归的拟合算法适用于处理复杂的非线性关系问题,尤其在需要拟合平滑曲线或曲面时表现尤为突出。同时,它也适用于对数据采样要求较高的问题,以及需要预测不确定性和概率分布的问题。然而,对于计算资源有限或对算法效率要求较高的问题,可能需要考虑其他更高效的算法。
高斯核回归拟合算法的原理主要基于高斯核函数和核方法。
首先,高斯核函数是一种特殊的核函数,它可以将输入数据映射到一个高维特征空间。高斯核函数具有一些重要的性质,例如对称性、正定性和可微性等。这些性质使得高斯核函数在处理非线性问题时具有很好的效果。
其次,核方法是一种通过核函数将输入数据映射到高维特征空间的方法。核方法的核心思想是将输入数据映射到高维特征空间,然后在这个高维空间中进行线性回归。由于高维特征空间中的数据点具有更好的线性可分性,因此可以更好地拟合数据。
在高斯核回归拟合算法中,首先使用高斯核函数将输入数据映射到一个高维特征空间,然后在高维特征空间中进行线性回归。在拟合过程中,通过最小化损失函数来拟合数据点的概率分布,从而得到回归模型。
高斯核回归拟合算法的优点包括能够处理复杂的非线性关系、能够给出预测的不确定性等。然而,该算法也存在一些缺点,例如计算复杂度高、对数据采样要求高等。
总之,高斯核回归拟合算法是一种处理复杂非线性关系的有效方法,适用于需要预测不确定性和概率分布的问题。然而,在应用时需要根据具体问题和数据特点进行选择和调整。
2 出图效果
附出图效果如下:

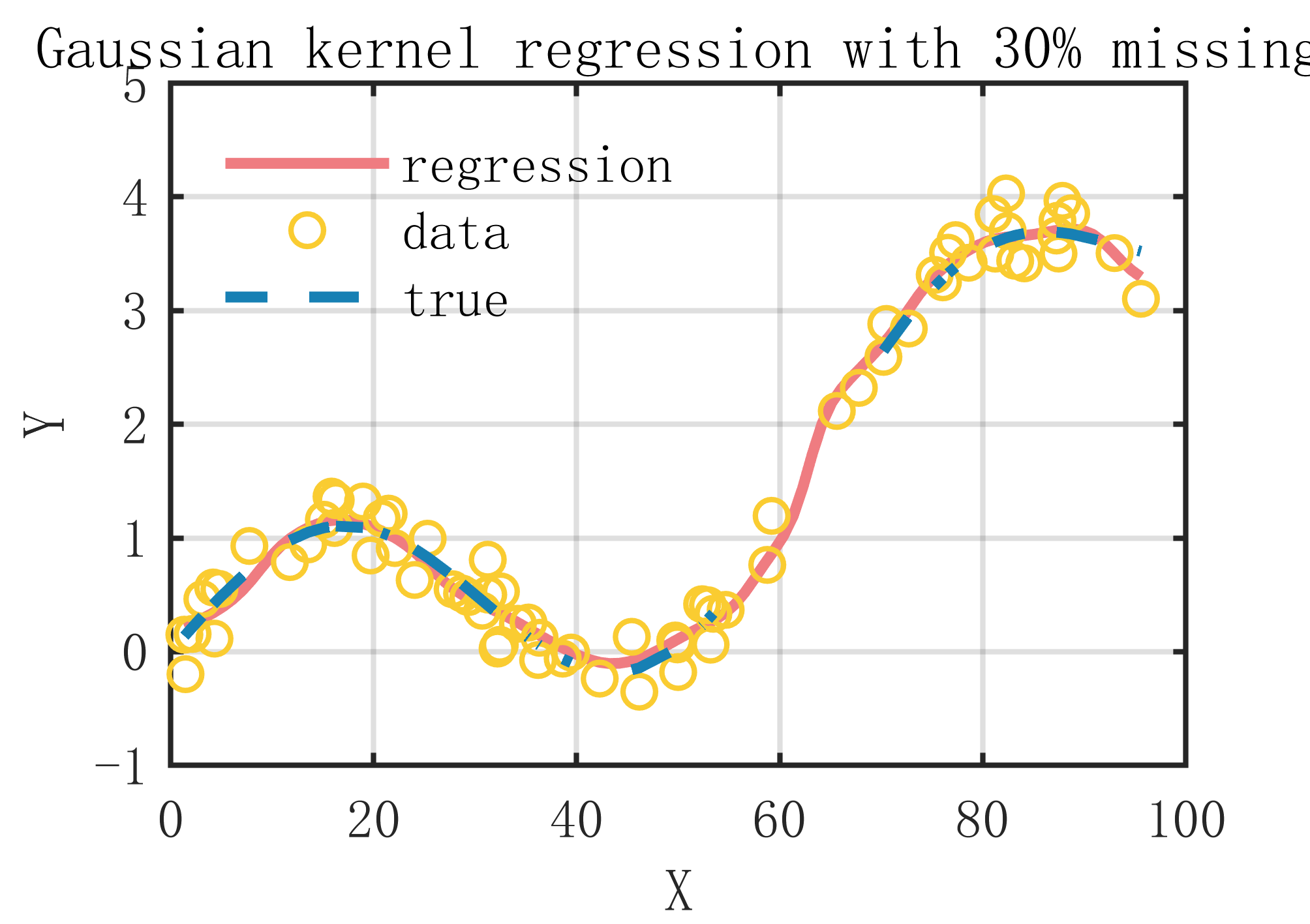
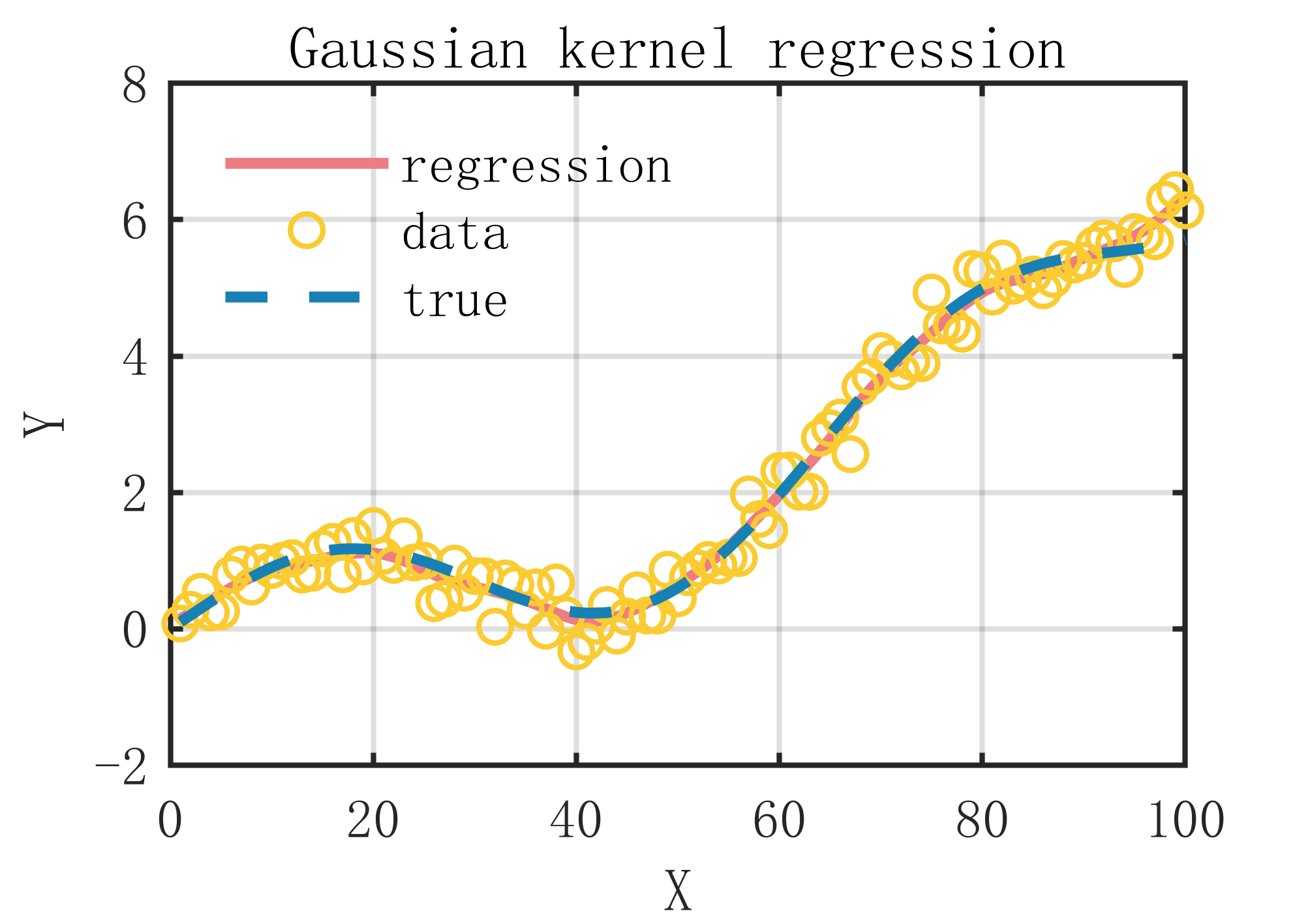
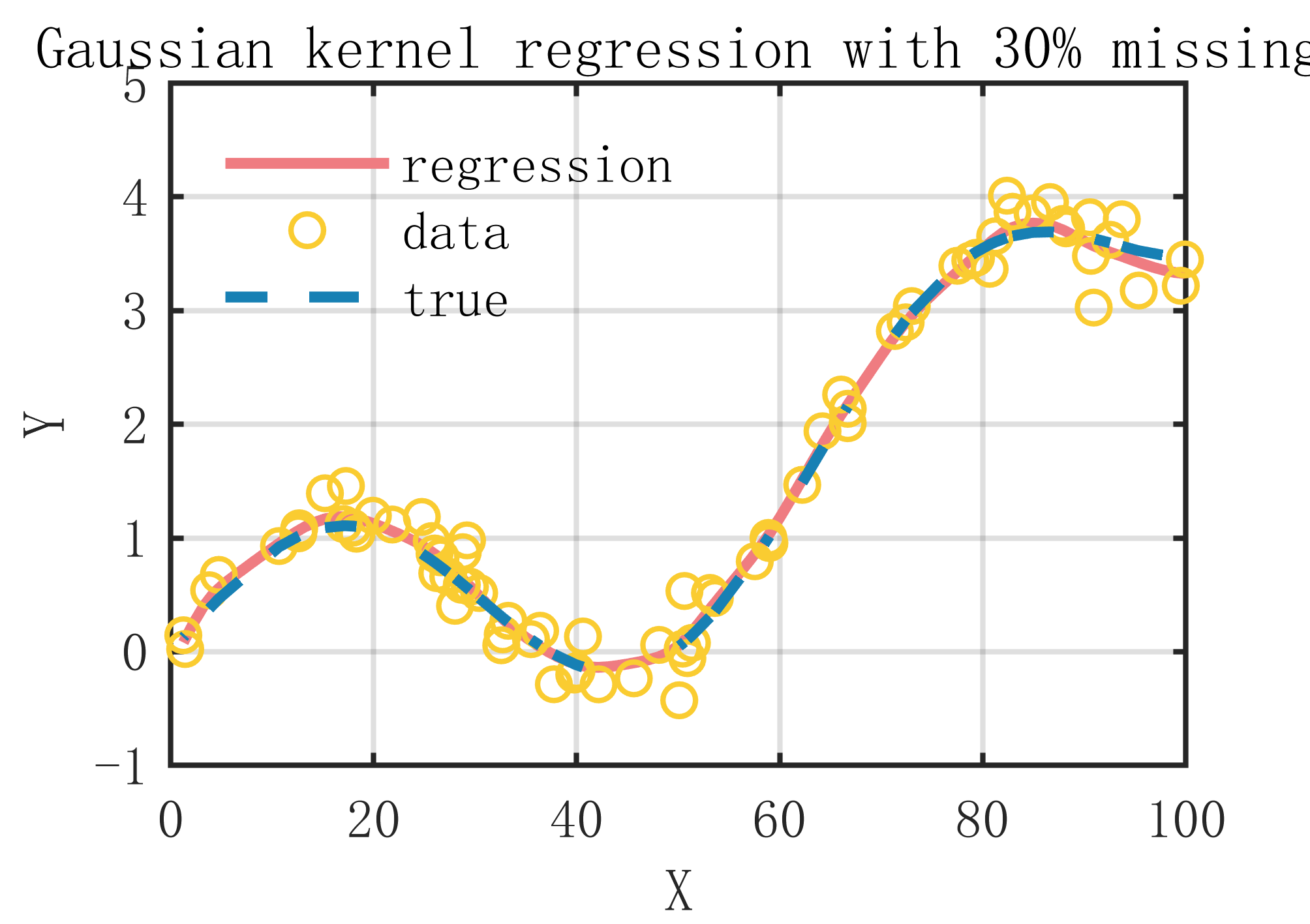
附视频教程操作:
【MATLAB】数据拟合第12期-基于高斯核回归的拟合算法
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- JavaScript读写NFC Ntag标签源码
- thingsboard规则引擎统计频率调整
- java 为什么使用多线程
- 如何修复卡在恢复模式的Android 手机并恢复丢失的数据
- [开发语言][C++]:递增递减运算符
- 【笔记】使用fetch进行流式数据接收,仿chatGPT智能对话,文字依次输入
- MySQL中的行锁、临建锁、间隙锁和表锁中的意向锁
- 迅为RK3568开发板-实时系统烧写(Preemption 系统/ Xenomai系统烧写)
- 系列四十一、MyBatis配置文件模板
- jQuery Ajax 缓存