BP神经网络

神经网络得典型结构

输入层：取决于输入样本的数量。假设m个样本，每个样本n个维度。

隐藏层：连接到输入层和输出层。神经元的个数自定义，无硬性要求。

输出层：神经网络的最终输出结果，可以用来分类和回归预测

用于拟合（预测）和分类

因此权值和阈值得确定尤为重要

接下来是神经元的信息传递

f是信号加工，建立x和y之间关系的过程

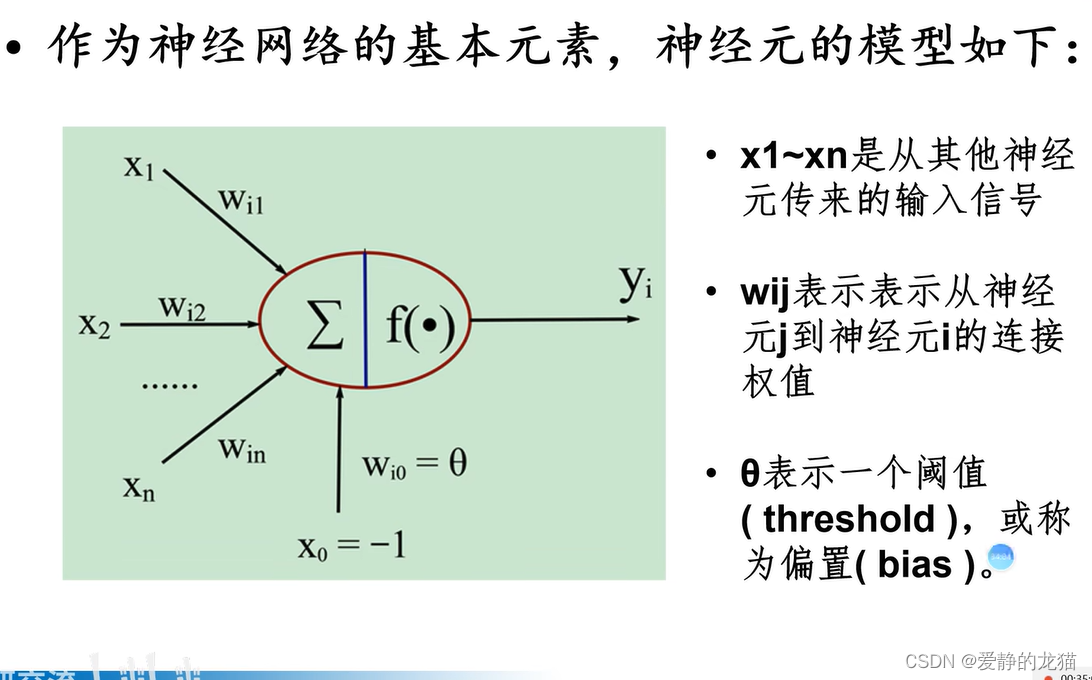
激活量和净激活量

激活函数是对净激活量与输出进行映射的函数

一般用这两个

网络模型分类

前馈

反馈

自组织

前馈没有反馈的，很容易造成大的误差，没有调整的过程，只往上传

工作状态

分为学习和工作两种状态

利用学习算法来调整神经元之间的连接权重，使得网络输出更符合实际

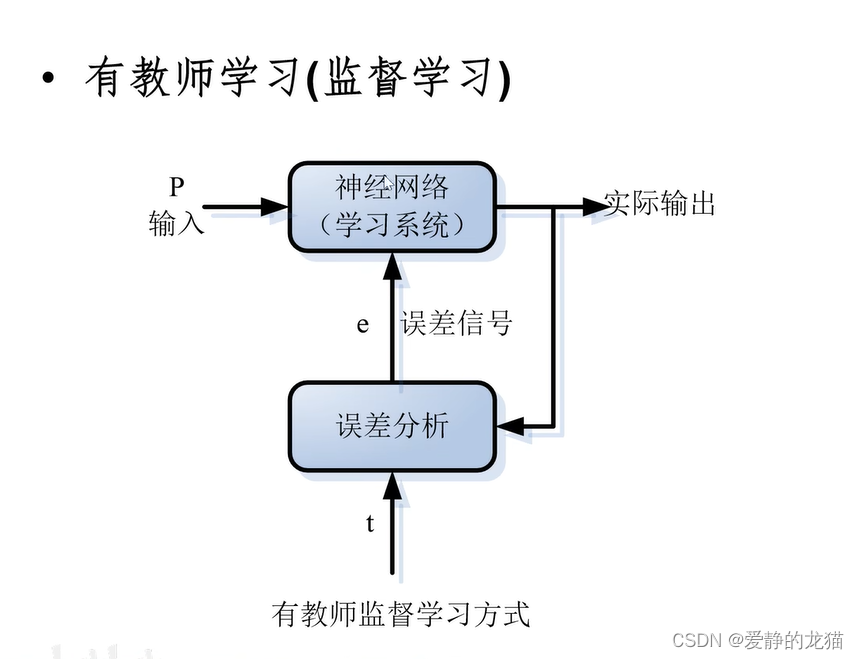
学习是有导师学习

把一组训练集送入网络，根据网络的实际输出与期望输出之间的差别来调整连接权。

工作

神经元之间的连接权值不变，可以作分类器或预测数据之用。

工作往往是在学习的基础之上进行的。

讲重头戏

BP算法

利用BP学习算法的前馈神经网络称为BP神经网络

什么是不固定的呢？

就是权值。

BP算法，利用输出后的误差估计输出层的直接前导层的误差，再用这个误差估计更前一层的误差，如此一层一层的反传下去，就获得了其他各层的误差估计。

信号是正向传播的。

误差反传，修复各神层单元的权值。

要求解模型

就是f(x)-A最小的时候，即是误差最小的

(A是实际值）

就是导函数的点（但是容易取得局部最优值）

标准输出-输出向量平方求和再×二分之一即可。

隐含层神经元需要用权值取×再求和

代入函数就可以求出隐含层输出

同理，输出层也是一样的