【42页动态规划学习笔记分享】动态规划核心原理详解及27道LeetCode相关经典题目汇总
????《博主简介》
小伙伴们好,我是阿旭。专注于人工智能AI、python、计算机视觉相关分享研究。
?更多学习资源,可关注公-仲-hao:【阿旭算法与机器学习】,共同学习交流~
👍感谢小伙伴们点赞、关注!
《------往期经典推荐------》
一、AI应用软件开发实战专栏【链接】
二、机器学习实战专栏【链接】,已更新31期,欢迎关注,持续更新中~~
三、深度学习【Pytorch】专栏【链接】
四、【Stable Diffusion绘画系列】专栏【链接】
《------正文------》
这篇文章是博主在学习动态规划系列算法过程中精心总结的42页学习笔记,其中包含了动态规划的原理详解以及LeetCode中的动态规划题目汇总。
免费分享给需要的下伙伴。原版文档获取方式见文末。
目录
 ?
?
介绍??
定义??
动态规划时一种运筹学方法,是在多轮决策过程中的最优方法。
应用场景??
动态规划问题的一般形式就是求最值。动态规划其实是运筹学的一种最优化方法,只不过在计算机问题上应用比较多,比如说让你求最长递增子序列呀,最小编辑距离呀等等。
核心??
求解动态规划的核心问题是穷举。因为要求最值,肯定要把所有可行的答案穷举出来,然后在其中找最值。
动态规划特点(三要素)??
1.最优子结构:原问题的最优解所包含的子问题的解也是最优的,通过子问题的最值得到原问题的最值。
2.存在重叠子问题:子问题间不独立(这是动态规划区别于分治的最大不同);如果暴力穷举的话效率会极其低下,所以需要「备忘录」或者「DP table」来优化穷举过程,避免不必要的计算
3.无后效性:即后续的结果不会影响当前结果。
通常的思考过程??
动态规划没有标准的解题方法,但在宏观上有通用的方法论:
下面的 k 表示多轮决策的第 k 轮
1.分阶段,将原问题划分成几个子问题。一个子问题就是多轮决策的一个阶段,它们可以是不满足独立性的。?? ?
2.找状态,选择合适的状态变量 Sk。它需要具备描述多轮决策过程的演变,更像是决策可能的结果。
3.做决策,确定决策变量 uk。每一轮的决策就是每一轮可能的决策动作,例如 D2 的可能的决策动作是 D2 -> E2 和 D2 -> E3。
4.状态转移方程。这个步骤是动态规划最重要的核心,即 sk+1= uk(sk)?。
5.定目标。写出代表多轮决策目标的指标函数 Vk,n。
6.寻找终止条件。
状态转移方程一般过程??
状态转移方程:一般思考过程,明确「状态」?->?定义 dp 数组/函数的含义?->?明确「选择」->?明确 base case。方程本质是数学的递推式
解题方法??
递归是一种自顶向下的求解方式,DP数组是一种自底向上的求解方式。
1.递归寻找暴力解:自顶向下求解;
2.通过备忘录memo优化递归过程,剔除重复计算,消除一下重叠子问题;
3.通过DP table?自底向上求解:主要是需要明确DP数组的含义定义,然后通过递推进行推导。
DP数组注意事项??
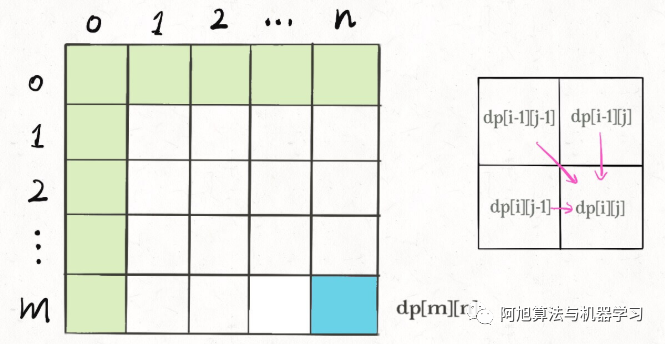
数组的遍历方向
| # 正向遍历 int[][] dp = new int[m][n]; for (int i = 0; i < m; i++)?? ? ? ? ????for?(int j = 0; j < n; j++) ????????//?计算 dp[i][j] # 反向遍历 for (int i = m - 1; i >= 0; i--) ????for?(int j = n - 1; j >= 0; j--) ????????//?计算 dp[i][j] # 斜向遍历 for (int l = 2; l <= n; l++) ????for?(int i = 0; i <= n - l; i++) ????????int?j = l + i - 1; ????????//?计算 dp[i][j] |
? ? ? ? ??
DP数组的递推计算过程需要注意两点:
1、遍历的过程中,所需的状态必须是已经计算出来的。
2、遍历的终点必须是存储结果的那个位置
主要就是看 base case 和最终结果的存储位置。
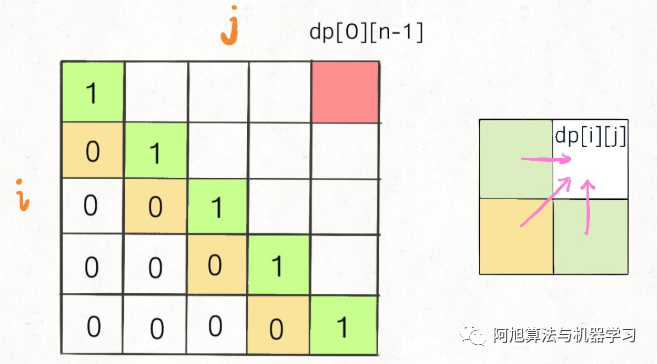
如:编辑距离问题:正向遍历?? ?
 ?
?
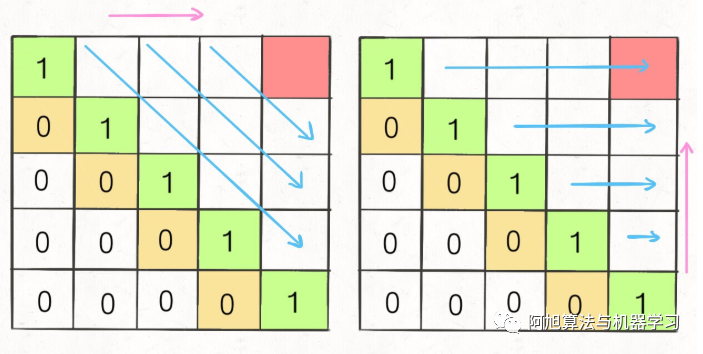
回文子序列问题:从左至右斜着遍历,或从下向上从左到右遍历,都可以
 ?
?
 ?
?
?? ?
举例??
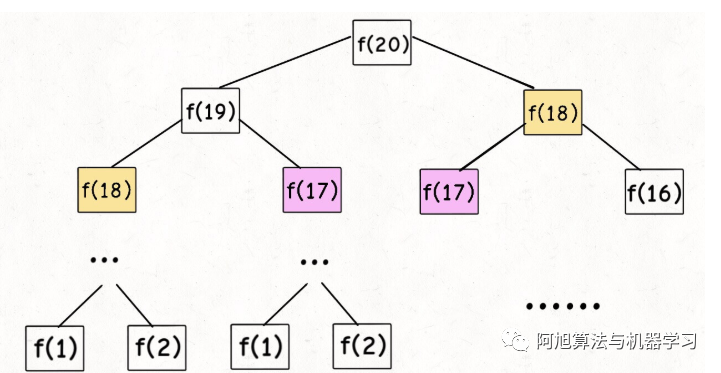
1.斐波拉契数列??
暴力递归:时间复杂度2^n指数级??
| def?fib(n): ????if?n?<=?2: ????????return?1 ????return?fib(n-1)?+?fib(n-2) |
 ?
?
带备忘录的递归??
| def?fib(n): ????def?helper(n): ????????if?n?<=?2: ????????????return?1 ????????if?n?in?memo: ????????????return?memo[n] ????????memo[n]?=?fib(n-1)?+?fib(n-2) ????????return?memo[n] ????memo?=?{} # 记录已经计算过的值,防止重复计算 ????return?helper(n) |
DP数组的迭代解法??
上述递归过程是自顶向下求解的,dp数组则是自底向上求解的。
| def?fib(n): ????dp?=?[0?for?_?in?range(n+1)]?? ? ? ? ????dp[1]?=?dp[2]?=?1 ????for?i?in?range(3, n?+?1): ????????dp[i]?=?dp[i-1]?+?dp[i-2] ????return?dp[n] |
根据斐波那契数列的状态转移方程,当前状态只和之前的两个状态有关,其实并不需要那么长的一个 DP table 来存储所有的状态,只要想办法存储之前的两个状态就行了。所以,可以进一步优化,把空间复杂度降为 O(1):
| def?fib(n): ????if?n?<=?2: ????????return?1 ????prev?=?1 ????curr?=?1 ????for?i?in?range(3,n+1): ????????prev,?curr?=?curr, prev?+?curr ????return?curr |
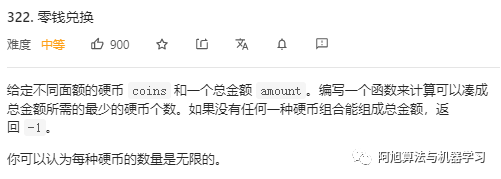
2.零钱兑换问题??
 ?
?
题目:给你?k?种面值的硬币,面值分别为?c1, c2 ... ck,每种硬币的数量无限,再给一个总金额?amount,问你最少需要几枚硬币凑出这个金额,如果不可能凑出,算法返回 -1 。
状态转移方程:
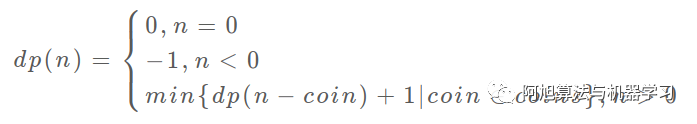 ?
?
| # 伪码框架 def coinChange(coins: List[int], amount: int):?? ? ? ? ????#?定义:要凑出金额 n,至少要 dp(n) 个硬币 ????def?dp(n): ????????#?做选择,选择需要硬币最少的那个结果 ????????for?coin in coins: ????????????res?= min(res, 1 + dp(n - coin)) ????????return?res ????#?我们要求的问题是 dp(amount) ????return?dp(amount) |
实际代码:
暴力解法??
| def?coinChange(coins, amount): ????def?dp(n): ????????# 函数定义为目标金额为n时,所需的最少硬币数量 ????????# base case ????????# 目标金额为 0 时,所需硬币数量为 0;当目标金额小于 0 时,无解,返回 -1 ????????if?n?==?0:?return?0 ????????if?n?<?0:?return?-1 ????????# 求最小值,所以初始化结果为正无穷 ????????res?=?float('inf') ????????for?coin?in?coins: ????????????subpro?=?dp(n-coin) ????????????if?subpro?==?-1: ????????????????# 子问题无解,跳过 ????????????????continue ????????????res?=?min(res,?1?+?subpro) ????????return?res?if?res?!=?float('inf')?else?-1 ????return?dp(amount) |
带备忘录的递归??
| def?coinChange(coins, amount):?? ? ? ? ????def?dp(n): ????????# 函数定义为目标金额为n时,所需的最少硬币数量 ????????# base case ????????# 目标金额为 0 时,所需硬币数量为 0;当目标金额小于 0 时,无解,返回 -1 ????????if?n?==?0:?return?0 ????????if?n?<?0:?return?-1 ????????if?n?in?memo: ????????????return?memo[n] ????????# 求最小值,所以初始化结果为正无穷 ????????res?=?float('inf') ????????for?coin?in?coins: ????????????subpro?=?dp(n-coin) ????????????if?subpro?==?-1: ????????????????# 子问题无解,跳过 ????????????????continue ????????????res?=?min(res,?1?+?subpro) ????????memo[n]?=?res?if?res?!=?float('inf')?else?-1 ????????return?memo[n] ????memo?=?{} ????return?dp(amount) |
DP数组迭代解法??
dp[i] = x?表示,当目标金额为?i?时,至少需要?x?枚硬币。
| def?coinChange(coins, amount): # 数组大小为 amount + 1,初始值也为 amount + 1 # 因为总的零钱个数不会超过amount,所以初始化amount + 1即可 ????dp?=?[amount?+?1?for?_?in?(amount?+?1)] ????dp[0]?=?0 ????for?i?in?range(len(dp)): ????????#??内层 for循环,求解的是所有子问题 + 1 的最小值 ????????for?coin?in?coins: ????????????# 子问题无解,跳过 ????????????if?i?-?coin?<?0: ????????????????continue ????????????dp[i]?=?min(dp[i],1+dp[i-coin])?? ? ? ? ????if?dp[amount]?==?amount?+?1: ????????return??-1 ????else: ????????return?dp[amount] |
注:dp?数组初始化为?amount + 1?呢,因为凑成?amount?金额的硬币数最多只可能等于?amount(全用 1 元面值的硬币),所以初始化为?amount + 1?就相当于初始化为正无穷,便于后续取最小值。
 ?
?
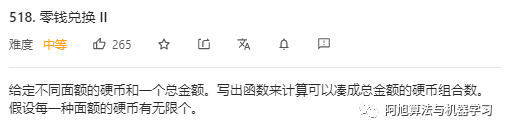
这个题目相当于是组合问题,每个硬币可以用多次,一共有多少种组合。
说明:前k个硬币凑齐金额i的组合数等于前k-1个硬币凑齐金额i的组合数加上在原来i-k的基础上使用硬币的组合数。说的更加直白一点,那就是用前k的硬币凑齐金额i,要分为两种情况开率,一种是没有用前k-1个硬币就凑齐了,一种是前面已经凑到了i-k,现在就差第k个硬币了。
DP[i] = DP[i] + DP[i-k]:
式子右边的DP[i]表示不使用第K个金币的和为i的组合, DP[i-k]表示使用金币k的和为i的组合数。
? ? ? ? ??
第 39 题问的是所有的组合列表,需要知道每一个组合是什么?,应该使用?回溯算法?求解,并且存储每一个组合;
第 518 题问的是组合有多少种,而不是问具体的解。应该使用?动态规划?求解
| class?Solution: ????def?change(self, amount:?int, coins:?List[int])?->?int:?? ? ? ? ????????# 子问题:对于硬币从0到k,我们必须使用第k个硬币的时候,当前金额的组合数 ????????# 状态数组DP[i]表示对于第k个硬币能凑的组合数 ????????# 转移方程DP[i] = DP[i] + DP[i-k] ????????dp?=?[0]?*?(amount?+?1) ????????dp[0]?=?1 ????????for?coin?in?coins: ????????????for?x?in?range(1,?amount?+?1): ?????????????????if?x < coin: continue???#?coin不能大于amount ????????????????dp[x]?+=?dp[x?-?coin] ????????return?dp[amount] |
 ?
?
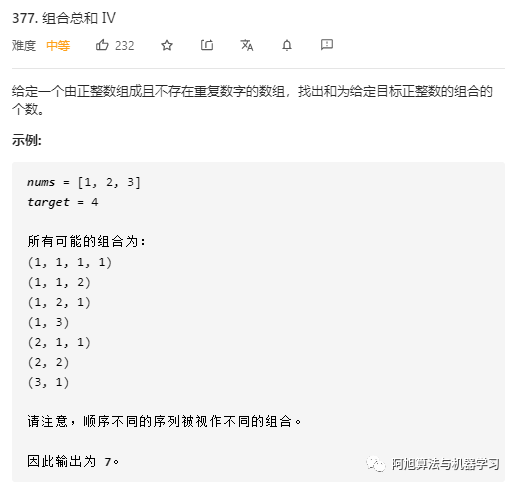
这个题实际上是排列问题,因为顺序不同的话视为不同的组合。
| class?Solution: ????def?combinationSum4(self, nums:?List[int],?target:?int)?->?int: ????????dp?=?[0]?*?(target?+?1)?? ? ? ? ????????dp[0]?=?1 ????????for?x?in?range(1, target?+?1): ????????????for?num?in?nums: ????????????????if?x?<?num:continue ????????????????dp[x]?+=?dp[x?-?num] ????????return?dp[target] |
? ? ? ? ??
参考:
https://leetcode-cn.com/problems/coin-change-2/solution/ling-qian-dui-huan-iihe-pa-lou-ti-wen-ti-dao-di-yo/
https://leetcode-cn.com/problems/coin-change-2/solution/ling-qian-dui-huan-ii-by-leetcode/
总结:
518零钱兑换2是一个组合问题,DP先遍历零钱列表,再遍历amount金额数;
| def?change(coins,amount): ????# 求的是组合数 ????dp?=?[0?for?_?in?range(amount+1)] ????dp[0]?=?1 ????for?coin?in?coins:??# 枚举硬币 ????????for?i?in?range(amount?+?1):??# 枚举金额 ????????????if?i?<?coin:?continue?#coin不能大于amount ????????????dp[i]?=?dp[i]?+?dp[i?-?coin] ????return?dp[amount] |
? ? ? ? ??
377组合个数是一个排列问题, DP先遍历amount金额数,再遍历零钱列表。
| def?change(coins,amount): ????# 求的是排列数 ????dp?=?[0?for?_?in?range(amount+1)] ????dp[0]?=?1?? ? ? ? ????for?i?in?range(amount?+?1):??# 枚举金额 ????????for?coin?in?coins:??#枚举硬币 ????????????if?i?<?coin:?continue?#coin不能大于amount ????????????dp[i]?=?dp[i]?+?dp[i?-?coin] ????return?dp[amount] |
举例:
在LeetCode上有两道题目非常类似,分别是
70.爬楼梯??--排列问题
518. 零钱兑换 II??-- 组合问题
如果我们把每次可走步数/零钱面额限制为[1,2], 把楼梯高度/总金额限制为3. 那么这两道题目就可以抽象成"给定[1,2], 求组合成3的组合数和排列数"。
爬台阶问题通用模板
| def?climbStairs(n): ????# 爬台阶问题通用模板 ????dp?=?[0?for?_?in?range(n?+?1)] ????dp[0]?=?1 ????steps?=?[1,2,4,5] ????for?i?in?range(n+1): ????????for?j?in?range(len(steps)): ????????????if?i?<?steps[j]:?continue?# 台阶少于跨越的步数 ????????????dp[i]?=?dp[i]?+?dp[i-steps[j]] ????return?dp[n] |
? ? ? ? ???? ?
经典题目??
*最长回文子串??
 ?
?
? ? ? ? ??
| # 动态规划 # 用 P(i,j)P(i,j) 表示字符串 s的第 i 到 j 个字母组成的串(下文表示成 s[i:j])是否为回文串 class?Solution: ????def?longestPalindrome(self, s:?str)?->?str: ????????n?=?len(s) ????????dp?=?[[False]?*?n?for?_?in?range(n)] ????????ans?=?"" ????????# 枚举子串的长度 l+1 ????????for?l?in?range(n): ????????????# 枚举子串的起始位置 i,这样可以通过 j=i+l 得到子串的结束位置 ????????????for?i?in?range(n-l): ????????????????j?=?i?+?l ????????????????if?l?==?0: ????????????????????dp[i][j]?=?True?? ? ? ? ????????????????elif?l?==?1: ????????????????????dp[i][j]?=?(s[i]?==?s[j]) ????????????????else: ????????????????????dp[i][j]?=?(dp[i?+?1][j?-?1]?and?s[i]?==?s[j]) ????????????????if?dp[i][j]?and?l?+?1?>?len(ans): ????????????????????ans?=?s[i:j+1] ????????return?ans ? ? ? ? ? ? ? ? ?? ? ? ? ? ? ? ? ? ?? # 中心扩展法 class?Solution: ????def?expandAroundCenter(self, s, left, right): ????????while?left?>=?0?and?right?<?len(s)?and?s[left]?==?s[right]: ????????????left?-=?1 ????????????right?+=?1 ????????return?left?+?1, right?-?1 ? ? ? ? ? ? ? ? ?? ????def?longestPalindrome(self, s:?str)?->?str: ????????# 中心扩展法,每个字符从中心往两边扩展,分奇偶 ????????start,?end?=?0,?0 ????????for?i?in?range(len(s)): ????????????left1,?right1?=?self.expandAroundCenter(s, i, i)?# 以当前字符为中心 ????????????left2,?right2?=?self.expandAroundCenter(s, i, i?+?1)?# 以当前字符与后面一个字符为中心 ????????????if?right1?-?left1?>?end?-?start: ????????????????start,?end?=?left1, right1 ????????????if?right2?-?left2?>?end?-?start: ????????????????start,?end?=?left2, right2 ????????return?s[start:?end?+?1] |
? ? ? ? ???? ?
*最长有效括号??
 ?
?
法一:动态规划
| class?Solution: ????def?longestValidParentheses(self, s:?str)?->?int: ????????# 动态规划 ????????# dp[i] 表示以i结尾的最长有效括号长度,‘(’对应的一定是0 ????????n?=?len(s) ????????if?n?==?0: ????????????return?0 ????????dp?=?[0]?*?n ????????for?i?in?range(1,n): ????????????#?i- dp[i-1] -1是与当前')'对称的位置 ????????????# dp[i-dp[i-1]-2] 表示与当前')'对称的位置前面的有效括号长度,需加上 ????????????if?s[i]==')'?and?i?-?dp[i-1]?-?1>=0?and?s[i?-?dp[i-1]?-?1]?==?'(': ????????????????dp[i]?=?dp[i-1]?+?dp[i-dp[i-1]-2]?+?2 ????????return?max(dp) |
? ? ? ? ??
法二:栈
| class?Solution: ????def?longestValidParentheses(self, s:?str)?->?int: ????????# 栈来实现 ????????stack?=?[-1] ????????length?=?0 ????????max_length?=?0?? ? ? ? ????????for?i?in?range(len(s)): ????????????if?s[i]?==?'(': ????????????????stack.append(i) ????????????else: ????????????????stack.pop() ????????????????if?not?stack: ????????????????# 栈为空,则添加当前右括号的索引入栈,为分割标识 ????????????????????stack.append(i) ????????????????else: ????????????????????length?=?i?-?stack[-1] ????????????????????max_length?=?max(max_length, length) ????????return?max_length |
? ? ? ? ??
*不同的子序列??
 ?
?
? ? ? ? ???? ?
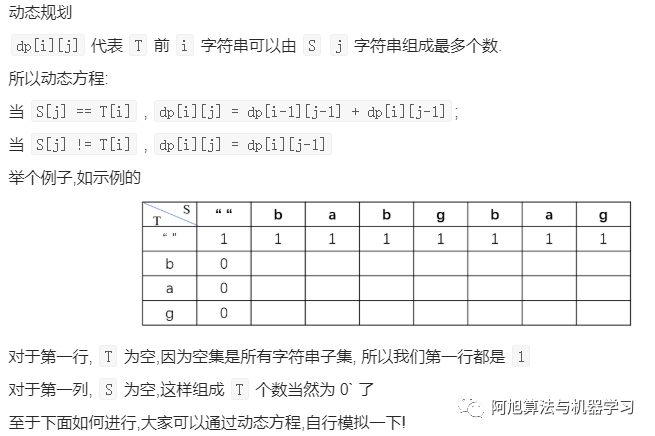 ?
?
| class?Solution: ????def?numDistinct(self, s:?str, t:?str)?->?int: ????????# S中T出现的个数 ????????# dp[i][j]表示t的前i个字符串可以由s的前j个字符串组成多少个 ????????n?=?len(s)?# 列 ????????m?=?len(t)?# 行 ????????dp?=?[[0]?*?(n+1)?for?_?in?range(m+1)] ????????for?j?in?range(n+1): ????????????dp[0][j]?=?1 ????????for?i?in?range(1,m?+?1): ????????????for?j?in?range(1, n?+?1): ????????????????if?t[i-1]?==?s[j-1]: # 对应于两种情况,s选择当前字母和不选择当前字母 # s选择当前字母dp[i-1][j-1] # s不选择当前字母 dp[i][j-1] ????????????????????dp[i][j]?=?dp[i-1][j-1]?+?dp[i][j-1] ????????????????else: ????????????????????dp[i][j]?=?dp[i][j-1] ????????return?dp[-1][-1] |
? ? ? ? ???? ?
? ? ? ? ??
*最长公共子序列??
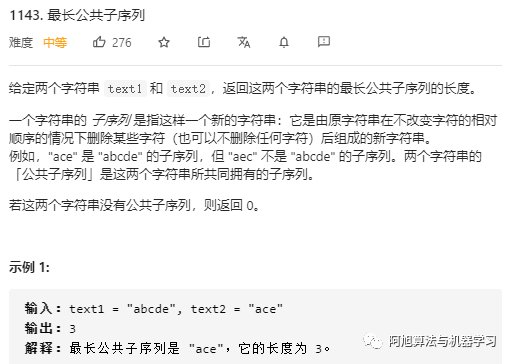 ?
?
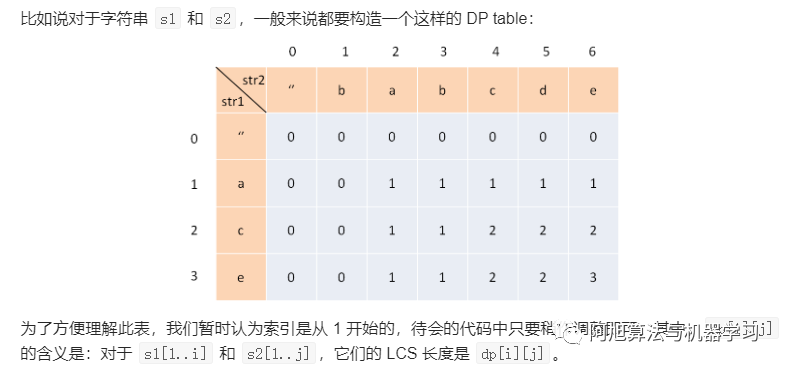 ?
?
参考:https://leetcode-cn.com/problems/longest-common-subsequence/solution/dong-tai-gui-hua-zhi-zui-chang-gong-gong-zi-xu-lie/?? ?
| # 动态规划 class?Solution: ????def?longestCommonSubsequence(self, text1:?str, text2:?str)?->?int: ????????m?=?len(text1) ????????n?=?len(text2) ????????dp?=?[[0]?*?(n?+?1)?for?_?in?range(m?+?1)] ????????for?i?in?range(1, m+1): ????????????for?j?in?range(1, n+1): ????????????????if?text1[i-1]?==?text2[j-1]: ????????????????????dp[i][j]?=?dp[i-1][j-1]?+?1 ????????????????else: ????????????????????dp[i][j]?=?max(dp[i][j-1],dp[i-1][j]) ????????return?dp[-1][-1] ? ? ? ? ? ? ? ? ?? # 递归 class?Solution: ????def?longestCommonSubsequence(self, text1:?str, text2:?str)?->?int: ????????# 递归 ????????memo?=?{}?#备忘录 ????????def?dp(i, j): ????????????if?i?==?-1?or?j?==?-1: ????????????????return?0 ????????????if?(i,j)?in?memo: ????????????????return?memo[(i,j)] ????????????if?text1[i]?==?text2[j]: ????????????????memo[(i,j)]?=?dp(i-1, j-1)?+?1 ????????????else: ????????????????memo[(i,j)]?=?max(dp(i-1, j),?dp(i,j-1)) ????????????return?memo[(i,j)] ????????return?dp(len(text1)-1,len(text2)-1) |
? ? ? ? ??
*最长公共子串??
注意:与子序列不相同的是子串是连续的,子序列可以是不连续的。?? ?
 ?
?
| def?LCS(s1,s2): ????#dp[i][j]表示以s1的i及s2的j结尾的最长公共子串长度 ????#如果s1[i-1] != s2[j-1] 则,dp[i][j] = 0 ????m?=?len(s1) ????n?=?len(s2) ????dp?=?[[0]?*(n+1)?for?_?in?range(m?+?1)] ????maxLen?=?0 ????end?=?0 ????for?i?in?range(1,m+1): ????????for?j?in?range(1,n+1): ????????????if?s1[i-1]?==?s2[j-1]: ????????????????dp[i][j]?=?dp[i-1][j-1]?+?1 ????????????else: ????????????????dp[i][j]?=?0 ????????????if?dp[i][j]?>?maxLen: ????????????????maxLen?=?dp[i][j] ????????????????end?=?j-1 ????if?maxLen?==?0: ????????return?'' ????else: ????????return?s2[end?-?maxLen?+?1:end?+?1] |
? ? ? ? ???? ?
? ? ? ? ??
*最长上升子序列??
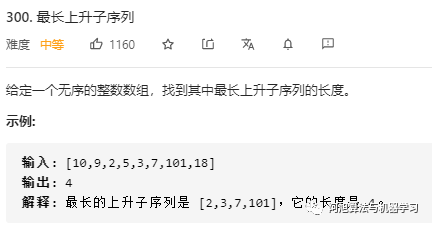 ?
?
| class?Solution: ????def?lengthOfLIS(self, nums:?List[int])?->?int: ????????if?not?nums: ????????????return?0 ????????# dp[i]表示以第i个元素结尾的最长递增子序列长度 ????????n?=?len(nums) ????????dp?=?[1?for?_?in?range(n)] ????????for?i?in?range(n): ????????????for?j?in?range(i): ????????????????if?nums[i]?>?nums[j]: ????????????????????dp[i]?=?max(dp[i],dp[j]?+?1) ????????return?max(dp) |
? ? ? ? ???? ?
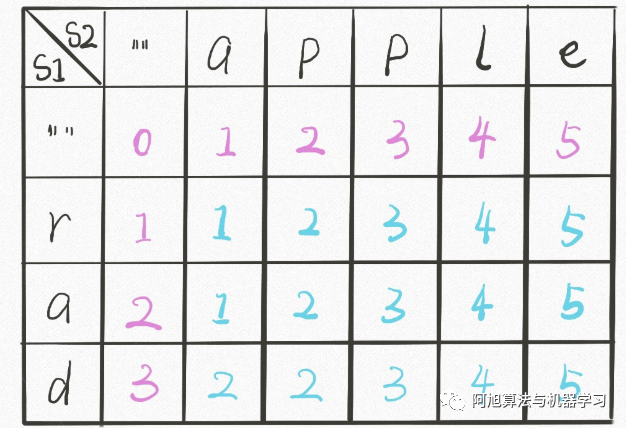
**编辑距离??
 ?
?
 ?
?
| class?Solution: ????def?minDistance(self, word1:?str, word2:?str)?->?int: ????????# DP递推方程?? ? ? ? ????????#?存储 s1[0..i] 和 s2[0..j] 的最小编辑距离 ????????m?=?len(word1) ????????n?=?len(word2) ????????dp?=?[[0]*(n+1)?for?i?in?range(m+1)] ????????for?i?in?range(m+1): ????????????dp[i][0]?=?i ????????for?j?in?range(n+1): ????????????dp[0][j]?=?j ????????for?i?in?range(1, m+1): ????????????for?j?in?range(1,n+1): ????????????????if?word1[i-1]?==?word2[j-1]: ????????????????????dp[i][j]?=?dp[i-1][j-1] ????????????????else: ????????????????????dp[i][j]?=?min(dp[i-1][j]+1, ????????????????????dp[i][j-1]+1, ????????????????????dp[i-1][j-1]+1) ????????return?dp[m][n] # 递归写法 class?Solution: ????def?minDistance(self, word1:?str, word2:?str)?->?int: ? ? ? ? ? ? ? ? ?? ????????def?dp(i,j): ????????????if?i?==?-1: ????????????????return?j?+?1 ????????????if?j?==?-1: ????????????????return?i?+?1 ????????????if?(i,j)?in?memo: ????????????????return?memo[(i,j)] ????????????if?word1[i]?==?word2[j]: ????????????????memo[(i,j)]?=?dp(i-1,j-1) ????????????else: ????????????????memo[(i,j)]?=?min(dp(i-1,j)+?1, ????????????????dp(i,j-1)?+?1, ????????????????dp(i-1,j-1)?+?1) ????????????return?memo[(i,j)] ????????memo?=?{} ????????res?=?dp(len(word1)-1,len(word2)-1) ????????return?res |
? ? ? ? ???? ?
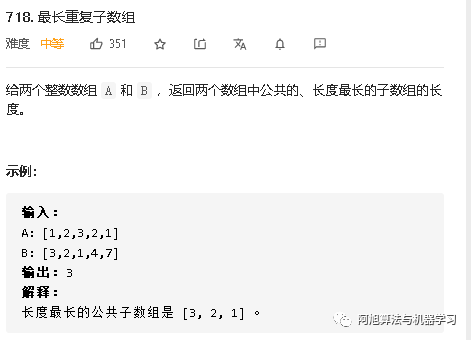
最长重复子数组??
 ?
?
| class?Solution: ????def?findLength(self, A:?List[int],?B:?List[int])?->?int: ????????# p[i][j] 表示 A[i:] 和 B[j:] 的最长公共前缀,那么答案即为所有 dp[i][j] 中的最大值。 ????????# 如果 A[i] == B[j],那么 dp[i][j] = dp[i + 1][j + 1] + 1,否则 dp[i][j] = 0。 ????????# 考虑到这里 dp[i][j] 的值从 dp[i + 1][j + 1] 转移得到,所以我们需要倒过来,首先计算 dp[len(A) - 1][len(B) - 1],最后计算 dp[0][0] ????????n,?m?=?len(A),?len(B) ????????dp?=?[[0]?*?(m?+?1)?for?_?in?range(n?+?1)] ????????ans?=?0 ????????for?i?in?range(n?-?1,?-1,?-1): ????????????for?j?in?range(m?-?1,?-1,?-1):?? ? ? ? ????????????????dp[i][j]?=?dp[i?+?1][j?+?1]?+?1?if?A[i]?==?B[j]?else?0 ????????????????ans?=?max(ans, dp[i][j]) ????????return?ans |
? ? ? ? ??
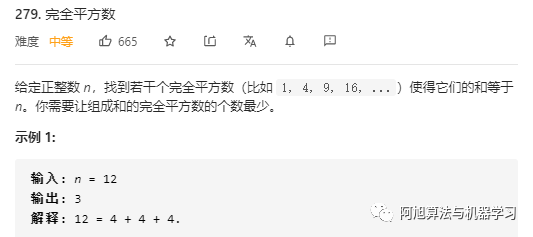
完全平方数??
 ?
?
| class?Solution: ????def?numSquares(self, n:?int)?->?int: ????????dp?=?[0]?*?(n?+?1) ????????for?i?in?range(1, n?+?1): ????????????dp[i]?=?i??#最坏的情况就是全是1 ????????????j?=?1 ????????????while?i?-?j*j?>=?0: ????????????????dp[i]?=?min(dp[i],?dp[i?-?j?*?j]?+?1) ????????????????j?+=?1 ????????return?dp[n] |
? ? ? ? ???? ?
不同路径1??
 ?
?
| class?Solution: ????def?uniquePaths(self, m:?int, n:?int)?->?int: ????????dp?=?[[0?for?i?in?range(n)]?for?_?in?range(m)] ????????for?i?in?range(m): ????????????dp[i][0]?=?1 ????????for?j?in?range(n): ????????????dp[0][j]?=?1 ????????for?i?in?range(1,m): ????????????for?j?in?range(1,n): ????????????????dp[i][j]?=?dp[i-1][j]?+?dp[i][j-1] ????????return?dp[-1][-1] |
不同路径2?? ?
 ?
?
| class?Solution: ????def?uniquePathsWithObstacles(self, obstacleGrid:?List[List[int]])?->?int: ????????m?=?len(obstacleGrid) ????????n?=?len(obstacleGrid[0]) ????????zero_loc?=?{(i,j)?for?i?in?range(m)?for?j?in?range(n)?if?obstacleGrid[i][j]?==?1} ????????dp?=?[[0]?*?n?for?i?in?range(m)] ????????for?i?in?range(m): ????????????# 初始化第一列,只要碰到一个1,那么后边都无法走到 ????????????if?obstacleGrid[i][0]?==?1: ????????????????break ????????????dp[i][0]?=?1 ????????for?j?in?range(n): ????????????#初始化第一行,只要碰到一个1,那么后边都无法走到 ????????????if?obstacleGrid[0][j]?==?1: ????????????????break ????????????dp[0][j]?=?1 ????????for?i?in?range(1,m): ????????????for?j?in?range(1,n): ????????????????if?(i,j)?in?zero_loc:?? ? ? ? ????????????????????dp[i][j]?=?0 ????????????????else: ????????????????????dp[i][j]?=?dp[i-1][j]?+?dp[i][j-1] ????????return?dp[-1][-1] ? ? ? ? ? ? ? ? ?? class?Solution: ????def?uniquePathsWithObstacles(self, obstacleGrid:?List[List[int]])?->?int: ????????m?=?len(obstacleGrid) ????????n?=len(obstacleGrid[0]) ????????if?obstacleGrid[0][0]?==?1?or?obstacleGrid[-1][-1]?==?1: ????????????return?0 ????????dp?=?[[0]?*?n?for?_?in?range(m)] ????????for?i?in?range(m): ????????????if?obstacleGrid[i][0]?==?0: ????????????????dp[i][0]?=?1 ????????????else: ????????????????break ????????for?j?in?range(n): ????????????if?obstacleGrid[0][j]?==?0: ????????????????dp[0][j]?=?1 ????????????else: ????????????????break ????????for?i?in?range(1,m): ????????????for?j?in?range(1,n):?? ? ? ? ????????????????if?obstacleGrid[i][j]?==?1: ????????????????????dp[i][j]?=?0 ????????????????????continue ????????????????dp[i][j]?=?dp[i-1][j]?+?dp[i][j-1] ????????return?dp[-1][-1] |
? ? ? ? ??
不同路径3(回溯)??
 ?
?
| class?Solution: ????def?uniquePathsIII(self, grid:?List[List[int]])?->?int: ????????# 注意每一个无障碍的格子都需要通过一次 ????????start_x?=?0?? ? ? ? ????????start_y?=?0 ????????steps?=?1 ????????m?=?len(grid) ????????n?=?len(grid[0]) ????????# 遍历获取起始位置和统计总步数 ????????for?i?in?range(m): ????????????for?j?in?range(n): ????????????????if?grid[i][j]?==?1: ????????????????????start_x?=?i ????????????????????start_y?=?j ????????????????????continue ????????????????if?grid[i][j]?==?0: ????????????????????steps?+=?1 ????????def?DFS(x,y,cur_step, grid): ????????????# 排除越界的情况和遇到障碍的情况 ????????????if?x?<?0?or?x?>=?m?or?y?<?0?or?y?>=?n?or?grid[x][y]?==?-1: ????????????????return?0 ????????????if?grid[x][y]?==?2: ????????????????# 走到2的位置,且步数为0,表示经过了所有的无障碍格子,是一种方案 ????????????????return?1?if?cur_step?==?0?else?0 ????????????grid[x][y]?=?-1?# 将已经走过的标记为障碍 ????????????res?=?DFS(x?-?1, y, cur_step?-?1, grid)?+?DFS(x?+?1, y, cur_step?-?1, grid)?\ ???????????????????+?DFS(x, y?-?1, cur_step?-?1, grid)?\ ???????????????????+?DFS(x, y?+?1, cur_step?-?1, grid) ????????????# 回溯 ????????????grid[x][y]?=?0 ????????????return?res ????????return?DFS(start_x,start_y,steps,grid) |
? ? ? ? ???? ?
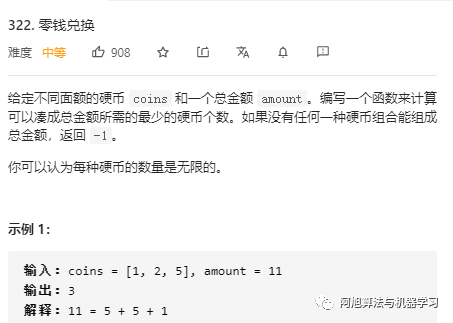
零钱兑换1??
 ?
?
| class?Solution: ????def?coinChange(self, coins:?List[int],?amount:?int)?->?int: ????????#dp[i] = x 表示金额i最少需要x个金币 ????????dp?=?[amount?+?1?for?i?in?range(amount?+?1)] ????????dp[0]?=?0 ????????for?i?in?range(amount+1): ????????????for?coin?in?coins: ????????????????if?i?-?coin?<?0: ????????????????????continue ????????????????dp[i]?=?min(dp[i],dp[i-coin]?+?1) ????????if?dp[amount]?==?amount?+?1: ????????????return?-1 ????????else: ????????????return?dp[amount] |
? ? ? ? ???? ?
零钱兑换2??
 ?
?
| class?Solution: ????def?change(self, amount:?int, coins:?List[int])?->?int: ????????# 子问题:对于硬币从0到k,我们必须使用第k个硬币的时候,当前金额的组合数 ????????# 状态数组DP[i]表示对于第k个硬币能凑的组合数 ????????# 转移方程DP[i] = DP[i] + DP[i-k] ????????dp?=?[0]?*?(amount?+?1) ????????dp[0]?=?1 ????????for?coin?in?coins: ????????????for?x?in?range(coin, amount?+?1): ????????????????dp[x]?+=?dp[x?-?coin] ????????return?dp[amount] |
最大正方形?? ?
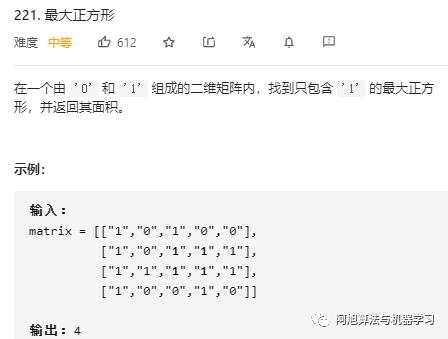 ?
?
| class?Solution: ????def?maximalSquare(self, matrix:?List[List[str]])?->?int: ????????# 用 dp(i, j) 表示以 (i, j)为右下角,且只包含 1的正方形的边长最大值 ????????if?len(matrix)?==?0?or?len(matrix[0])?==?0: ????????????return?0 ????????maxSide?=?0 ????????rows,?columns?=?len(matrix),?len(matrix[0]) ????????dp?=?[[0]?*?columns?for?_?in?range(rows)] ????????for?i?in?range(rows): ????????????for?j?in?range(columns): ????????????????if?matrix[i][j]?==?'1': ????????????????????if?i?==?0?or?j?==?0: ????????????????????????dp[i][j]?=?1 ????????????????????else: ????????????????????????dp[i][j]?=?min(dp[i?-?1][j],?dp[i][j?-?1],?dp[i?-?1][j?-?1])?+?1 ????????????????????maxSide?=?max(maxSide, dp[i][j]) ????????maxSquare?=?maxSide?*?maxSide ????????return?maxSquare |
? ? ? ? ???? ?
最大矩形??
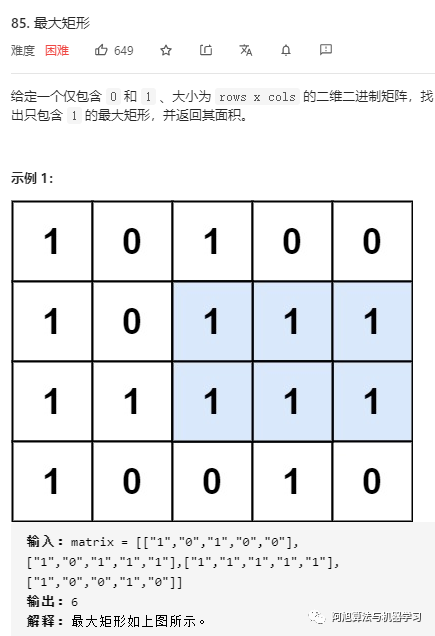 ?
?
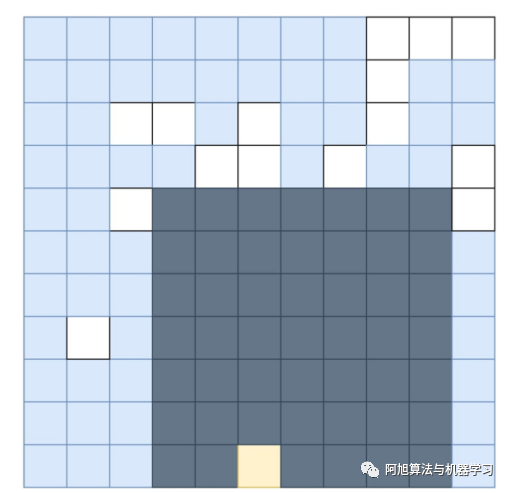 ?
?
| class?Solution: ????def?maximalRectangle(self, matrix:?List[List[str]])?->?int: ????????#时间复杂度 : O(NM)。每次对于N的迭代我们会对M迭代常数次 ????????if?not?matrix:?return?0 ????????m?=?len(matrix) ????????n?=?len(matrix[0]) ? ? ? ? ? ? ? ? ?? ????????left?=?[0]?*?n?# initialize left as the leftmost boundary possible ????????right?=?[n]?*?n?# initialize right as the rightmost boundary possible ????????height?=?[0]?*?n ????????maxarea?=?0 ????????for?i?in?range(m): ????????????cur_left,?cur_right?=?0, n ????????????# update height ????????????for?j?in?range(n): ????????????????if?matrix[i][j]?==?'1':?height[j]?+=?1 ????????????????else:?height[j]?=?0 ????????????# update left?? ? ? ? ????????????for?j?in?range(n): ????????????????if?matrix[i][j]?==?'1':?left[j]?=?max(left[j],?cur_left) ????????????????else: ????????????????????left[j]?=?0 ????????????????????cur_left?=?j?+?1 ????????????# update right ????????????for?j?in?range(n-1,?-1,?-1): ????????????????if?matrix[i][j]?==?'1':?right[j]?=?min(right[j],?cur_right) ????????????????else: ????????????????????right[j]?=?n ????????????????????cur_right?=?j ????????????# update the area ????????????for?j?in?range(n): ????????????????maxarea?=?max(maxarea, height[j]?*?(right[j]?-?left[j])) ? ? ? ? ? ? ? ? ?? ????????return?maxarea |
? ? ? ? ??
? ? ? ? ??
最大子序和??
 ?
?
| class?Solution: ????def?maxSubArray(self, nums:?List[int])?->?int: ????????# dp[i] 表示以小标i为结尾的最大连续子序列的和dp[j] = max(nums[j],dp[j-1] + nums[j]) ????????if?len(nums)?==?0: ????????????return?0 ????????if?len(nums)?==?1: ????????????return?nums[0] ????????n?=?len(nums)?? ? ? ? ????????dp?=?[float('-inf')]?*?n ????????dp[0]?=?nums[0] ????????for?j?in?range(1,n): ????????????dp[j]?=?max(nums[j],dp[j-1]?+?nums[j]) ????????return?max(dp) |
三角形最小路径和??
 ?
?
| #法一 class?Solution: ????def?minimumTotal(self, triangle:?List[List[int]])?->?int: ????????n?=?len(triangle) ????????f?=?[[0]?*?n?for?_?in?range(n)] ????????f[0][0]?=?triangle[0][0] ? ? ? ? ? ? ? ? ?? ????????for?i?in?range(1, n):?? ? ? ? ????????????f[i][0]?=?f[i?-?1][0]?+?triangle[i][0] ????????????for?j?in?range(1, i): ????????????????f[i][j]?=?min(f[i?-?1][j?-?1],?f[i?-?1][j])?+?triangle[i][j] ????????????f[i][i]?=?f[i?-?1][i?-?1]?+?triangle[i][i]????? ????????return?min(f[n?-?1]) ? ? ? ? ? ? ? ? ?? #法二 class?Solution: ????def?minimumTotal(self, triangle:?List[List[int]])?->?int: ????????n?=?len(triangle) ????????f?=?[0]?*?n ????????f[0]?=?triangle[0][0] ? ? ? ? ? ? ? ? ?? ????????for?i?in?range(1, n): ????????????f[i]?=?f[i?-?1]?+?triangle[i][i] ????????????for?j?in?range(i?-?1,?0,?-1): ????????????????f[j]?=?min(f[j?-?1],?f[j])?+?triangle[i][j] ????????????f[0]?+=?triangle[i][0] ????????return?min(f) |
? ? ? ? ??
? ? ? ? ???? ?
乘积最大子数组??
 ?
?
| class?Solution: ????def?maxProduct(self,?nums:?List[int])?->?int: ????????n?=?len(nums) ????????if?n?==?0: ????????????return?0 ????????dpMax?=?[float('-inf')]?*?n??#?存储以i结尾的最大连续子数组乘积 ????????dpMax[0]?=?nums[0] ????????dpMin?=?[float('inf')]?*?n?#?存储以i结尾的最小连续子数组乘积,存在负负得正的情况 ????????dpMin[0]?=?nums[0] ????????for?i?in?range(1,n): ????????????dpMax[i]?=?max(dpMin[i?-?1]?*?nums[i],?dpMax[i?-?1]?*?nums[i],?nums[i]) ????????????dpMin[i]?=?min(dpMin[i?-?1]?*?nums[i],?dpMax[i?-?1]?*?nums[i],?nums[i]) ????????return?max(dpMax) |
? ? ? ? ???? ?
打家劫舍??
 ?
?
| class?Solution: ????def?rob(self, nums:?List[int])?->?int: ????????#dp[i] 表示前 i间房屋能偷窃到的最高总金额 ????????#dp[i]?=?max(dp[i-1],dp[i-2]+nums[i])? ????????n?=?len(nums) ????????if?n==0: ????????????return?0 ????????if?n==1: ????????????return?nums[0] ????????dp?=?[0]*?n ????????dp[0]?=?nums[0] ????????dp[1]?=?max(nums[0],nums[1]) ????????for?i?in?range(2,n): ????????????dp[i]?=?max(dp[i-1],dp[i-2]+nums[i]) ????????return?dp[n-1] |
? ? ? ? ???? ?
最小路径和??
 ?
?
| class?Solution: def?minPathSum(self, grid:?List[List[int]])?->?int: ????#?dp[i][j]表示达到i,j点的最小路径和 ????????m?=?len(grid) ????????n?=?len(grid[0]) ????????dp?=?[[0]*n?for?_?in?range(m)] ????????dp[0][0]?=?grid[0][0] ????????for?i?in?range(1, m): ????????????dp[i][0]?=?dp[i-1][0]?+?grid[i][0] ????????for?i?in?range(1, n): ????????????dp[0][i]?=?dp[0][i-1]?+?grid[0][i] ????????for?i?in?range(1, m): ????????????for?j?in?range(1, n): ????????????????dp[i][j]?=?min(dp[i][j-1],?dp[i-1][j])?+?grid[i][j] ????????return?dp[-1][-1] |
? ? ? ? ???? ?
买卖股票问题??
 ?
?
| # 动态规划 ?class?Solution: ????def?maxProfit(self, prices:?List[int])?->?int: ????????# 动态规划dp[i] 表示前 i 天的最大利润 ????????n?=?len(prices) ????????if?n?==?0:?return?0?# 边界条件 ????????dp?=?[0]?*?n ????????minprice?=?prices[0] ????????for?i?in?range(1, n): ????????????minprice?=?min(minprice, prices[i]) ????????????dp[i]?=?max(dp[i?-?1],?prices[i]?-?minprice) ????????return?dp[-1] ? ? ? ? ? ? ? ? ?? # 方法二 def?maxProfit(self, prices:?List[int])?->?int: ????minprice?=?float('inf')?# 正无穷??负无穷 float("-inf") ????maxprofit?=?0 ????for?p?in?prices: ????????minprice?=?min(minprice, p) ????????maxprofit?=?max(maxprofit, p-minprice) ????return?maxprofit |
买卖股票的最佳时机2?? ?
 ?
?
? ? ? ? ??
| def?maxProfit(self, prices:?List[int])?->?int: ????#在第二次买的时候,价格其实是考虑用了第一次赚的钱去补贴一部分的 ????buy_1?=?buy_2?=?float('inf')?# 第一二次买之前的最低价 ????pro_1?=?pro_2?=?0 ??? ????for?p?in?prices: ????????buy_1?=?min(buy_1, p) ????????pro_1?=?max(pro_1, p?-?buy_1) ????????buy_2?=?min(buy_2, p?-?pro_1)?# p - pro_1 是用第一次的钱抵消了一部分第二次买的钱 ????????pro_2?=?max(pro_2, p?-?buy_2) ????return?pro_2 ? ? ? ? ? ? ? ? ?? |
? ? ? ? ???? ?
使用最小花费爬楼梯??
 ?
?
| class?Solution: ????def?minCostClimbingStairs(self, cost:?List[int])?->?int: ????????# 踏上第i级台阶的最小花费,用dp[i]表示 ????????# 初始条件: ????????# 最后一步踏上第0级台阶,最小花费dp[0] = cost[0]。 ????????# 最后一步踏上第1级台阶有两个选择: ????????# 可以分别踏上第0级与第1级台阶,花费cost[0] + cost[1]; ????????# 也可以从地面开始迈两步直接踏上第1级台阶,花费cost[1]。 ????????n?=?len(cost) ????????dp?=?[0]?*?n ????????dp[0],?dp[1]?=?cost[0],?cost[1] ????????for?i?in?range(2, n): ????????????dp[i]?=?min(dp[i?-?2],?dp[i?-?1])?+?cost[i] ????????return?min(dp[-2],?dp[-1]) |
? ? ? ? ???? ?
解码方法??
 ?
?
 ?
?
| class?Solution: ????def?numDecodings(self, s:?str)?->?int: ????????if?s[0]?==?'0': ????????????return?0 ????????n?=?len(s) ????????dp?=?[0]?*?(n?+?1) ????????dp[0]?=?1 ????????dp[-1]?=?1 ????????for?i?in?range(1,n): ????????????# '0'只有10和20才有对应字母,不然 返回 0?? ? ? ? ????????????if?s[i]?==?'0': ????????????????if?s[i-1]=='1'?or?s[i-1]=='2': ????????????????????dp[i]?=?dp[i-2] ????????????????else: ????????????????????return?0 ????????????else: ????????????????if?s[i-1]?==?'1'?or?(s[i-1]?=='2'?and?s[i]?<?'7'): ????????????????????# i-1与i 可以结合或者分开 ????????????????????dp[i]?=?dp[i-1]?+?dp[i-2] ????????????????else: ????????????????????# i-1与i 必须分开 ????????????????????dp[i]?=?dp[i-1] ????????return?dp[-2] |
? ? ? ? ???? ?
赛车??
 ?
?
?? ?
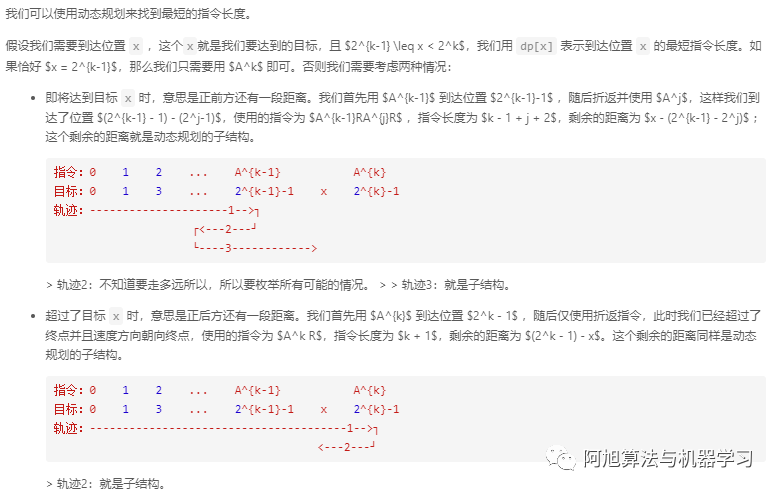 ?
?
![]() ?
?
 ?
?
?? ?
| # 动态规划 DP class?Solution(object): ????def?racecar(self, target): ????????# dp[x] 表示到达位置 x 的最短指令长度 ????????dp?=?[0,?1]?+?[float('inf')]?*?target ????????for?t?in?range(2, target?+?1): ????????????k?=?t.bit_length() ????????????if?t?==?2**k?-?1: ????????????????dp[t]?=?k ????????????????continue ????????????for?j?in?range(k?-?1): ????????????????# t - (2**(k-1)-2**j) 为剩余距离,dp[t - 2**(k - 1) + 2**j]表示这个剩余距离需要使用的最少命令数,加上已经使用的 k - 1 + j + 2 ????????????????# 由于返回使用的j不确定,因此需要通过遍历【0,k-2】确定dp[t]的最小值?? ? ? ? ????????????????dp[t]?=?min(dp[t],?dp[t?-?2**(k?-?1)?+?2**j]?+?k?-?1?+?j?+?2) ????????????# 2**k - 1 - t 表示剩余需要按返回的距离,dp[2**k - 1 - t]表示走剩余距离需要要使用的最少命令数,加上已经使用的k+1 ????????????dp[t]?=?min(dp[t],?dp[2**k?-?1?-?t]?+?k?+?1) ????????return?dp[target] ? ? ? ? ? ? ? ? ?? # 递归写法 class?Solution: ????dp?=?{0:?0} ????def?racecar(self, target:?int)?->?int: ????????t?=?target ????????if?t?in?self.dp: ????????????return?self.dp[t] ????????n?=?t.bit_length() ????????if?2**n?-?1?==?t: ????????????self.dp[t]?=?n ????????else: ????????????self.dp[t]?=?self.racecar(2**n?-?1?-?t)?+?n?+?1 ????????????for?m?in?range(n?-?1): ????????????????self.dp[t]?=?min(self.dp[t],?self.racecar(t?-?2**(n?-?1)?+?2**m)?+?n?+?m?+?1) ????????return?self.dp[t] |
? ? ? ? ??
? ? ? ? ???? ?
播放列表的数量??
 ?
?
| class?Solution: ????def?numMusicPlaylists(self, N:?int, L:?int, K:?int)?->?int: ????????mod?=?10?**?9?+?7 ????????# dp[i][j] 表示用j首不同的歌填充长度为i的歌单数目 ????????dp?=?[[0]?*?(N?+?1)?for?_?in?range(L?+?1)] ????????dp[0][0]?=?1 ????????for?i?in?range(1, L?+?1): ????????????for?j?in?range(1, N?+?1): ????????????????# 分成两种情况,我们可以播放没有播放过的歌也可以是播放过的 ????????????????# 如果当前的歌和前面的都不一样,歌单前i-1首歌只包括了j-1首不同的歌曲, ????????????????# 那么当前的选择有dp[i-1][j-1] * (N-j+1) ????????????????# 如果不是,那么就是选择之前的一首歌,之前最近的K首是不能选的,只能选择j-K前面的歌曲,(j 首歌,最近的 K 首不可以播放) ????????????????# 所以选择就是dp[i-1][j] * max(0, j-K)?? ? ? ? ????????????????dp[i][j]?=?(dp[i-1][j-1]?*?(N?-?j?+?1)?+?dp[i-1][j]?*?max(0, j?-?K))?%?mod ????????return?dp[-1][-1] |
? ?
关于本篇文章大家有任何建议或意见,欢迎在评论区留言交流!
觉得不错的小伙伴,感谢点赞、关注加收藏哦!
欢迎关注下方GZH:阿旭算法与机器学习,发送:【动态规划】,即可获取原版文档。欢迎小伙伴共同学习交流~
? ? ???? ?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Windows 10如何关闭系统自动更新(实用教程)
- Rust开发环境搭建
- 设计模式之避免共享的设计模式Immutability(不变性)模式
- 初学电音制作用FL Studio21怎么进行混音编曲?
- Linux下找到网络端口并杀死
- 基于CTF探讨Web漏洞的利用与防范
- 如何在水经微图中加载调用长光卫星影像
- 十三、W5100S/W5500+RP2040之MicroPython开发<MQTT&新版OneNET示例>
- 【Mybatis-Plus】mybatisplus更新时,实体字段为空,数据库不更新的解决方案
- 微信小程序map组件如何使用?