利用矩阵特征值解决微分方程

目录

一. 特征值介绍

二. 单变量常微分方程

三. 利用矩阵解决微分方程问题

四. 小结

4.1 矩阵论

4.2 特征值与特征向量内涵

4.3 应用

---

一. 特征值介绍

线性代数有两大基础问题：

如果A为对角阵的话，那么问题就很好解决。需要注意的是，矩阵的基础行变换会改变特征值的大小。

在已知解的情况下，可以利用矩阵行列式解决问题。根据Cramer定则：

将以下矩阵的行列式看成一个多项式：

该多项式的根即为特征值。当矩阵维度较高时，这个方法就很难计算。

二. 单变量常微分方程

假定某函数为u(t)，其中t为自变量，满足如下微分方程：

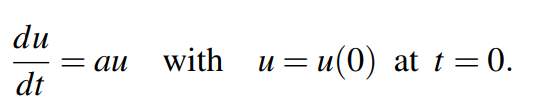
回忆：

很容易求出该单变量常微分方程的解为：

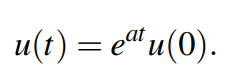
当a大于0，函数无界（unstable）；当a等于0，函数为常函数（stable）；当a小于0时，函数趋近于0（stable）；

当a为复数时，如下：

实数部分的分析与以上类似。虚数部分则会产生振荡，如下：

三. 利用矩阵解决微分方程问题

给出以下常微分方程问题：

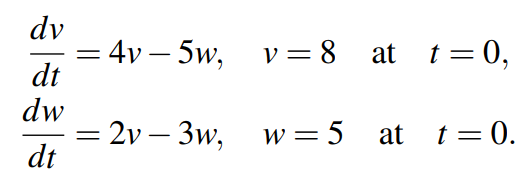
因为初始条件都是t=0，所以这类问题又被称之为初值问题（initial value problem），其中初值在这个地方指的就是8和5。

如果将t看成时间的话，该问题的本质则是寻找v(t)和w(t)，其中t大于0

一个常微分方程问题是怎么样跟矩阵联系在一起的呢？

首先，我们将两个未知的函数写成向量的形式，叫做u(t)，如下：

那么初始值则是u(0)，如下：

系数矩阵叫做A，如下：

那么原始的两个微分方程则可以合并成一个向量形式的微分方程，如下：

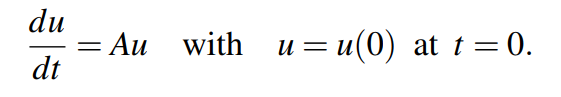
很明显这是一阶求导的方程，整个运算都是线性关系。系数均为常数结构，也就是矩阵A与时间t无关。

根据经验，v(t)和w(t)均为指数函数的结果，如果可以设两个函数的形式如下：

将两者合并为向量形式，如下：

很明显该结果满足我们想要的du/dt=Au的结构。将函数和带入原微分方程中，可得：

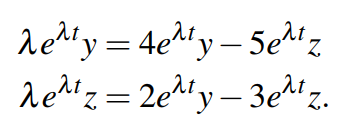
可以发现这两个方程都出现了，可以直接约简。这个时候最神奇的地方就出现了，当约简完后，你会发现：

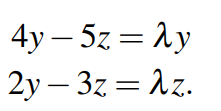
这不就是特征值方程！形式如下：

该特征值方程A已知，和x未知。也就是为矩阵A的特征值，x为矩阵A的特征向量。接下来就可以直接利用我们熟悉的线性代数知识直接求解即可。

四. 小结

4.1 矩阵论

矩阵论是一个重要的数学分支，属于代数学范畴，需要抽象思维能力、数学建模能力以及科学计算能力。目前矩阵论的思想方法已经渗透到网络安全、经济管理以及军事学等各个领域，尤其是上世纪五六十年代以来，随着计算机科学技术的发展，网络工程、信息工程、测绘工程以及密码工程等各个专业都需要利用矩阵论课。矩阵论包括线性空间与线性变换、矩阵的范数理论、矩阵分析、矩阵分解、矩阵的特征值估计以及矩阵的广义逆等。

矩阵论有几个细节很重要，比如特征值理论、线性空间和线性变换、矩阵运算、多项式理论等，然后将其应用于行列式的计算、矩阵的初等变换以线性方程组解的判定和解的结构等。借助数值计算软件 matlab等，可以用来建立数学模型，然后构建算法，利用科学计算方法最终解决实际问题。

方阵的特征值与特征向量是一个重要的数学概念，在数据处理的统计方法、通信网络中的信息检索、图像压缩与恢复、机械振动等多个方面都有广泛的应用，例如，工程技术中的振动问题和稳定性问题，在数值上大都归结为矩阵的特征值与特征向量的问题。

4.2 特征值与特征向量内涵

矩阵的特征值和特征向量定义高度抽象，设 A 是 n 阶方阵，若存在数λ 和 n 维非零向量 x，使得 Ax = λx 成立，则称数λ 是方阵 A 的特征值，非零向量 x 为方阵 A 的特征向量。

这个时候可以引入谱分解定理。

设矩阵A可以做如下分解：

其中矩阵P的列是A的单位正交特征向量：

相应的特征值为:

可以将这n个特征值形成n阶的对角阵。因为矩阵P为单位正交矩阵，所以可得：

由此以上可得：

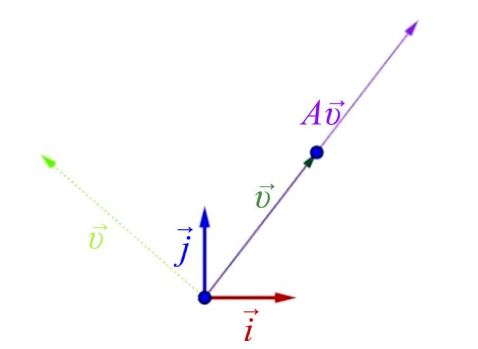
由上述定义可知，方阵的特征向量是经过矩阵变换后，保持方向不变，只是进行长度扩大或者缩小的向量，而特征值反映了特征向量在矩阵变换时的扩大或者缩小的倍数。结合谱分解定理可得，一个方阵完全可以由它的特征向量表示，特征值即是方阵在对应特征方向上的贡献率大小，即一个方阵可由特征值与特征向量组成的“特征”来表示，特征向量的几何直观如图 下所示：

4.3 应用

矩阵的各种分解形式为矩阵的科学计算提供了强有力的理论支撑，通过矩阵分解可以达到对矩阵进行降维的目的，从而减小内存量，简化运算。这时特征值与特征向量可以应用于图像压缩技术。

假定一幅图像有 m*n个像素，如果将这 mn 个数据一起传送，往往数据量会很大。因此，我们考虑在信息的发送端传送比较少的数据，并且在接收端利用这些传送数据对图像进行重构。这就是图像压缩的最初想法，不过图像压缩要求较高的压缩比，同时不产生失真。矩阵的奇异值分解可以将任意一个矩阵和一个只包含几个(非零)奇异值的矩阵对应。把“大”的矩阵对应到“小”的矩阵，这就产生了“压缩”的思想，并且利用矩阵的计算可以恢复压缩前的数据。