【动态规划】12简单多状态dp问题_打家劫舍II_C++ (medium)
题目链接:leetcode打家劫舍II
目录
题目解析:

题目让我们求在不触动警报装置的情况下?,能够偷窃到的最高金额。
由题可得:
第一个房屋和最后一个房屋是紧挨着的
如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警?(所以不能偷相邻的位置)
我们用示例二分析:
因为第一个房屋和最后一个房屋是紧挨着的
所以如果我们在这里选了第一个,那么第二个和最后一个就不能选。
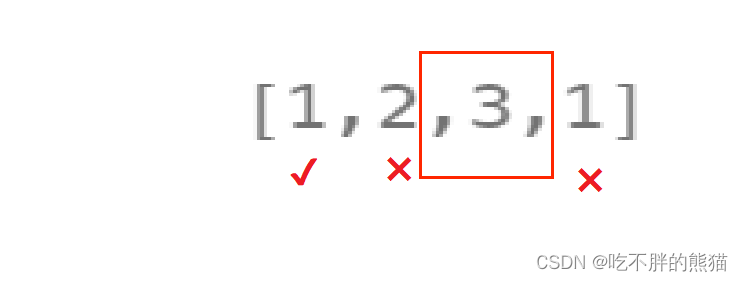
此时我们就只能在第三个和n-1个中选择;
如果我们在这里不选第一个,那么最后一个就能选。

此时我们就只能在第二个和n个中选择;
算法原理:
1.状态表示
先创建一个dp表
首先先思考dp表里面的值所表示的含义(是什么?)
因为我们这里的每个位置可以选或者不选,
所以这里我们一个位置就有两种状态
这里就要创建两个dp表来表示这两种状态:
f[i]表示到i位置选,此时到i位置能够偷窃到的最高金额;
g[i]表示到i位置不选,此时到i位置能够偷窃到的最高金额;
这种状态表示怎么来的?
1.经验+题目要求
用之前或者之后的状态,推导出dp[i][j]的值;
根据最近的最近的一步,来划分问题
经验:以i位置为结尾;
题目让我们求能够偷窃到的最高金额,且该位置可选可不选
这里我们需要用两个表来同时表示这种状态;
2.状态转移方程
dp[i]等于什么?
?因为i位置可选可不选,所有两种情况:
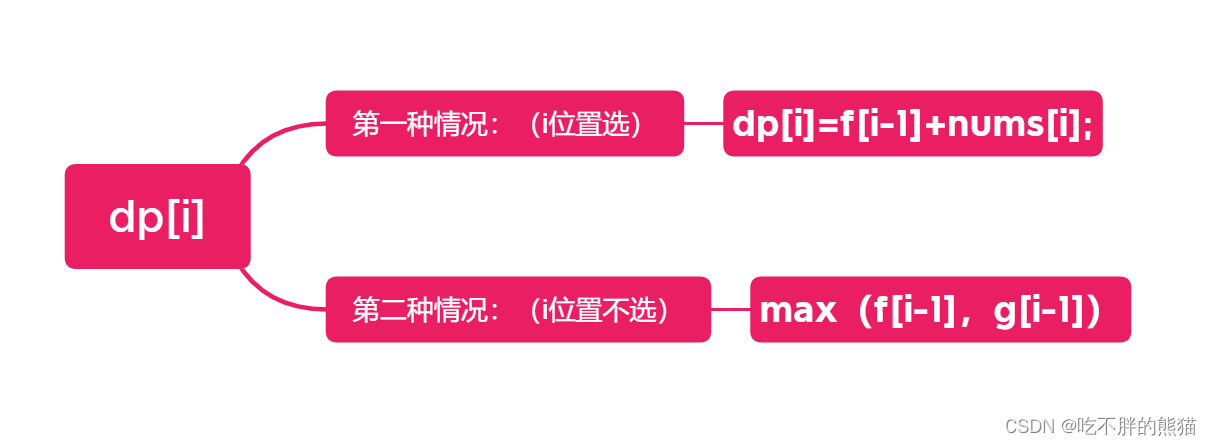
第一种情况:(i位置选)
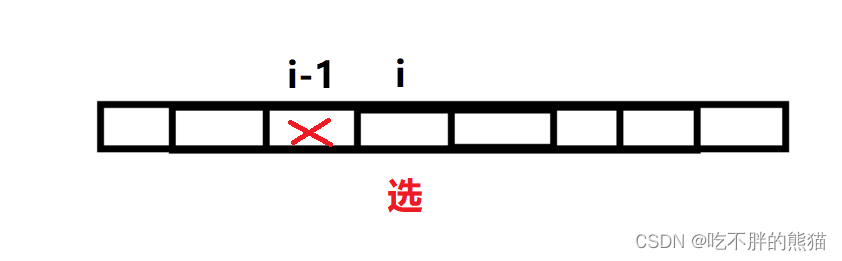
那么i-1位置必然不选:
此时我们只要知道在i-1之前所能够偷窃到的最高金额(g[i-1])+i位置的金额(nums[i])
所以这种情况下的状态转移方程为:
dp[i]=f[i-1]+nums[i];
第二种情况:(i位置不选)
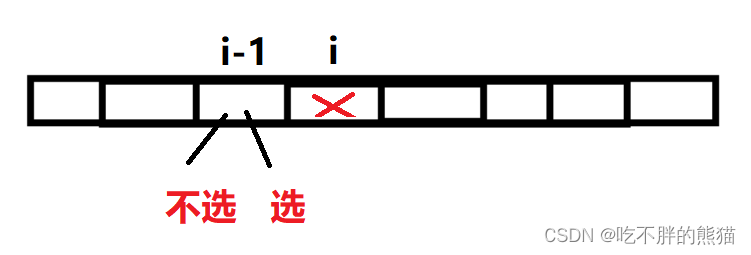
那么i-1位置可以选也可以不选,
这里会分两种情况:
情况a:(i-1选)
此时我们只要知道在i-1之前所能够偷窃到的最高金额(f[i-1])
所以这种情况下的状态转移方程为:
dp[i]=f[i-1];
情况b:(i-1不选)
此时我们只要知道在i-1之前所能够偷窃到的最高金额(g[i-1])
所以这种情况下的状态转移方程为:
dp[i]=g[i-1];
最后取a,b情况的最大值:max(f[i-1],g[i-1])
综上:
3.初始化
(保证填表的时候不越界)
由状态转移方程得:
我们在f[0]和g[0]会越界,所以需要把这两个位置初始化;
当第一个位置选,那么它能够偷窃到的最高金额f[0]为该位置的时长(f[0]=nums[0]);
当第一个位置不选,那么它能够偷窃到的最高金额g[0]为0(g[0]=0);
4.填表顺序
(为了填写当前状态的时候,所需要的状态已经计算过了)
这里所需要的状态是:
这里所需要的状态是:i-1
所以填表顺序:从左到右
5.返回值
(根据题目要求和状态表示)
综上分析:
最后一个位置可选可不选,所以返回这两个状态的最小值
返回值为:max(f[n-1],g[n-1]);
编写代码:

class Solution {
public:
int rob(vector<int>& nums) {
//1.创建dp表
//2.初始化
//3.填表
//4.返回结果
int n=nums.size();
return max(rod1(nums,2,n-2)+nums[0],rod1(nums,1,n-1));
}
int rod1(vector<int>& nums,int left,int right)
{
//处理边界问题
if(left>right)
return 0;
int n=nums.size();
vector<int> f(n);
auto g=f;
f[left]=nums[left];
for(int i=left;i<=right;i++)
{
f[i]=g[i-1]+nums[i];
g[i]=max(f[i-1],g[i-1]);
}
return max(f[right],g[right]);
}
};本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!