论文阅读：基于MCMC的能量模型最大似然学习剖析

On the Anatomy of MCMC-Based Maximum Likelihood Learning of Energy-Based Models

本文只介绍关于MCMC训练的部分，由此可知，MCMC常常被用于训练EBM。最后一张图源于Implicit Generation and Modeling with Energy-Based Models

本研究调查了马尔可夫链蒙特卡罗 (MCMC) 采样在无监督最大似然 (ML) 学习中的效果。 我们的注意力仅限于非归一化概率密度族，其中负对数密度（或能量函数）是 ConvNet。 我们发现，之前研究中用于稳定训练的许多技术都是不必要的。 具有 ConvNet 潜力的 ML 学习只需要几个超参数，并且不需要正则化。 使用这个最小框架，我们确定了仅取决于 MCMC 采样实施的各种 ML 学习成果。

一方面，我们表明训练基于能量的模型很容易，该模型可以使用短期 Langevin 对真实图像进行采样。 即使 MCMC 样本在整个训练过程中比真正的稳态样本具有更高的能量，ML 也可以是有效且稳定的。 基于这一见解，我们引入了一种 ML 方法，该方法具有纯噪声初始化的 MCMC、高质量短期合成，以及与具有信息性 MCMC 初始化（例如 CD 或 PCD）的 ML 相同的预算。 与以前的模型不同，我们的能量模型可以在训练后从噪声信号中获得真实的高多样性样本。

另一方面，使用非收敛 MCMC 学习的 ConvNet 势不具有有效的稳态，并且不能被视为近似训练数据的非标准化密度，因为长期运行的 MCMC 样本与观察到的图像有很大差异。 我们表明，训练 ConvNet 学习真实图像稳态的潜力要困难得多。 据我们所知，所有先前模型的长期 MCMC 样本都失去了短期样本的真实性。 通过正确调整 Langevin 噪声，我们训练了第一个 ConvNet 电位，其中长期和稳态 MCMC 样本是真实图像。

1 Introduction

1.1 诊断基于能量的模型

高维信号的统计建模是许多学科和实际应用中遇到的一项具有挑战性的任务。 我们在这项工作中研究图像信号。 当图像没有注释或标签时，深度监督学习的有效工具就无法应用，而必须使用无监督技术。 这项工作重点关注具有 ConvNet 势函数 (2) 的基于能量的模型 (1) 的无监督范式。

之前研究ConvNet势的最大似然（ML）训练的工作，例如（Xie et al. 2016；2018a；Gao et al. 2018），在学习过程中使用Langevin MCMC样本来近似未知且棘手的对数划分函数的梯度。 作者普遍发现，经过足够的模型更新后，短期 Langevin 从信息初始化（参见第 2.3 节）生成的 MCMC 样本是与数据相似的真实图像。

图 2：Oxford Flowers 102 数据集从数据样本到亚稳态样本的长期 MH 调整 Langevin 路径。 使用算法 1 的两种变体来训练模型：使用来自噪声初始化的 $L=100$ MCMC 步骤训练的非收敛 ML（顶部），以及使用来自持久初始化的 $L=500$ MCMC 步骤训练的收敛 ML（底部）。

然而，我们发现，无论 MCMC 初始化、网络结构和辅助训练参数如何，先前工作学习的能量函数都存在重大缺陷。先前所有实现的能量函数的长期和稳态 MCMC 样本都是过饱和图像，具有显着的过饱和图像。 能量低于观测到的数据（见图 2 顶部和图 3）。 在这种情况下，将学习模型描述为训练集的近似密度是不合适的，因为该模型将不成比例的高概率质量分配给与观察数据显着不同的图像。 高质量短期样本和低质量长期样本之间的系统差异是一个关键现象，但在之前的研究中似乎没有被注意到。

图 3：近期基于能量的模型的长期 Langevin 样本。 概率质量集中在具有不真实外观的图像上。 从左到右：牛津花上的 Wasserstein-GAN 评论家（Arjovsky、Chintala 和 Bottou，2017 年）、牛津花上的 WINN（Lee 等人，2018 年）、ImageNet 上的条件 EBM（Du 和 Mordatch，2019 年）。 W-GAN 批评者并未接受非标准化密度训练，但我们提供了样本以供参考。

1.2 Our Contributions

在这项工作中，我们提出了对通过基于 MCMC 的 ML 学习 ConvNet 潜力的基本理解。 我们诊断学习过程中出现的以前未识别的并发症，并提炼我们的见解来训练具有新功能的模型。 我们的主要贡献是：

• 识别两个不同的轴，它们表征基于MCMC的ML学习中的每个参数更新：1）正负样本的能量差异，以及2）MCMC收敛或不收敛。 与普遍预期相反，高质量合成不需要收敛。 参见图 1 和第 3 节。
• 第一个 ConvNet 势是使用 ML 和纯噪声初始化 MCMC 进行训练的。 与之前的模型不同，我们的模型在仅根据噪声进行训练后可以有效地生成真实且多样化的样本。 参见图 7。我们的配套工作（Nijkamp 等人，2019）进一步探讨了这种方法。
• 第一个具有真实稳态样本的 ConvNet 潜力。 据我们所知，所有以前的训练实现都无法获得在图像空间中具有真实 MCMC 采样的 ConvNet 潜力。 我们参考（Kumar et al. 2019）进行讨论。 请参见图 2（底部）和图 8（中栏和右栏）。
• 利用磁化能量景观中的扩散来映射图像空间能量函数的宏观结构，以进行无监督的簇发现。 见图9

1.3 Related Work

基于能量的图像模型 基于能量的模型定义状态空间上的非归一化概率密度，以表示给定系统中的状态分布。 Hopfield 网络（Hopfield 1982）将 Ising 能量模型改编为能够表示任意观测数据的模型。 RBM（受限玻尔兹曼机）（Hinton 2012）和 FRAME（滤波器、随机场和最大熵）（Zhu、Wu 和 Mumford 1998；Wu、Zhu 和 Liu 2000）模型引入了具有更大表征能力的能量函数。 RBM 使用与可观察图像像素具有联合密度的隐藏单元。 FRAME模型使用卷积滤波器和直方图匹配来学习数据特征。

开创性的工作（Hinton 等人，2006）研究了基于能量的分层模型。 （Ngiam 等人，2011）是一项重要的早期工作，提出了前馈神经网络来模拟能量函数。 (2) 形式的基于能量的模型在 (Dai, Lu, and Wu 2015) 中介绍。 FRAME 模型的深度变体（Xie 等人，2016 年；Lu、Zhu 和 Wu，2016 年）是第一个通过 ConvNet 势和 Langevin 采样实现真实合成的模型。 (Du and Mordatch 2019) 中应用了类似的方法。多网格模型（Gao et al. 2018）学习不同尺度图像的 ConvNet 势的集合。 (Kim and Bengio 2016; Dai et al. 2017; Xie et al. 2018b; 2018a; Han et al. 2019; Kumar et al. 2019) 中探讨了使用生成器网络作为近似直接采样器来学习 ConvNet 势。 这些作品（Jin、Lazarow 和 Tu 2017；Lazarow、Jin 和 Tu 2017；Lee 等人 2018）在判别框架中学习 ConvNet 潜力。

尽管其中许多工作声称将能量 (2) 训练为观察图像的近似非标准化密度，但生成的能量函数不具有反映数据的稳态（见图 3）。 来自信息初始化的短期 Langevin 样本呈现为近似稳态样本，但进一步的研究表明长期 Langevin 始终破坏短期图像的真实性。 我们的工作首先是解决和纠正所有先前实现的系统性不收敛问题。

2. Learning Energy-Based Models

在本节中，我们回顾了先前作品中基于 MCMC 的 ML 学习的既定原则（Hinton 2002；Zhu、Wu 和 Mumford 1998；Xie 等人 2016）。

2.1 Maximum Likelihood Estimation

基于能量的模型是吉布斯-玻尔兹曼密度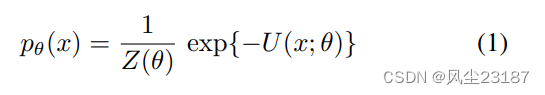

在信号 $x\in X?R^N$ 上。 势能 $U(x;\theta )$ 属于参数族 u = { U ( ? ; θ ) : θ ∈ θ } u = \{U(· ; θ) : θ ∈ θ\} u={U(?;θ):θ∈θ}。 棘手的常数 $Z(\theta )$ 从未被明确使用，因为势 $U(x;\theta )$ 为 MCMC 采样提供了足够的信息。 在本文中，我们将注意力集中在形式为的能量势上

其中 $F(x;\theta )$ 是具有单个输出通道和权重 $\theta \in R^D$ 的卷积神经网络.
在机器学习中，我们寻求找到 $\theta \in \Theta$，使得参数模型 $p_{\theta }(x)$ 非常接近数据分布 $q(x)$。 衡量接近程度的一种方法是 KullbackLeibler (KL) 散度。 学习通过解决问题来进行

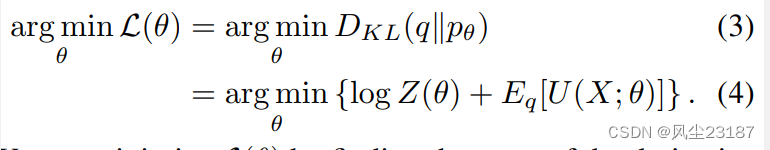
我们可以通过求导数的根来最小化 $L(\theta )$

其中 { X i + } i = 1 n \{X^+_i \} ^n_{i=1} {Xi+?}i=1n? 是 $i.i.d.$ 来自数据分布 $q$ 的样本（称为正样本，因为概率增加），并且 { X i ? } i = 1 m \{X^?_i \} ^m_{i=1} {Xi??}i=1m? 是 $i.i.d$ 来自当前学习分布 $p_{\theta }$ 的样本（称为负样本，因为概率降低了）。 实际上，正样本 { X i + } i = 1 n \{X^+_i \} ^n_{i=1} {Xi+?}i=1n?是一批训练图像，负样本 { X i ? } i = 1 m \{X^?_i \} ^m_{i=1} {Xi??}i=1m? 是经过$L$ 次MCMC采样迭代后得到的。