二叉树简介
发布时间:2024年01月15日
二叉树
二叉树是每个节点最多有两个子树的树结构,通常子树被称作“左子树”和“右子树”。
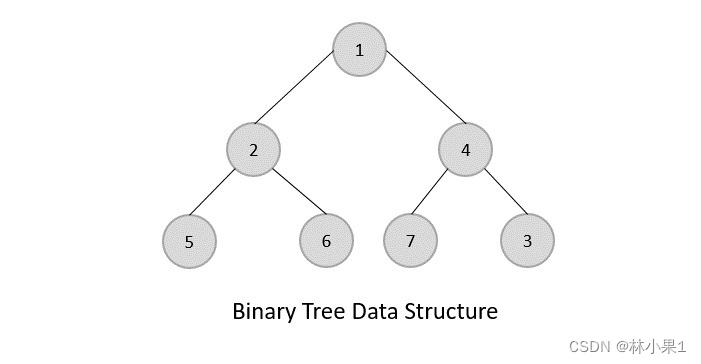
二叉树的遍历
二叉树的遍历主要有三种方式:前序遍历、中序遍历和后序遍历。
- 前序遍历:访问根节点 --> 遍历左子树 --> 遍历右子树
- 中序遍历:遍历左子树 --> 访问根节点 --> 遍历右子树
- 后序遍历:遍历左子树 --> 遍历右子树 --> 访问根节点
二叉树的实现
初始化二叉树
我们首先定义一个数组 arr 来存储二叉树的节点。然后在构造函数中,我们检查数组是否为空,如果为空则抛出异常。
public class ArrayBinaryTree<E> {
private E[] arr;
public ArrayBinaryTree(E[] arr){
if(arr.length == 0)
throw new IllegalArgumentException("数组不能为空");
this.arr = arr;
}
}
前序遍历
前序遍历的顺序是:访问根节点 --> 遍历左子树 --> 遍历右子树。下图展示了前序遍历的过程。
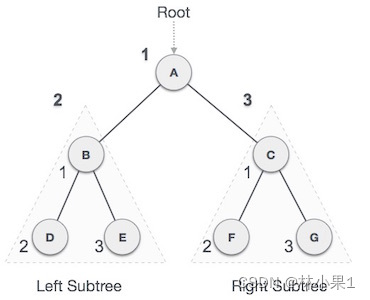
我们使用 preOrder 方法来实现前序遍历。该方法接受一个索引和一个结果列表作为参数,然后将遍历的结果添加到结果列表中。
public void preOrder(int index, List<E> result){
result.add(arr[index]);
if(2 * index + 1 < arr.length){
preOrder(2 * index + 1,result);
}
if(2 * index + 2 < arr.length){
preOrder(2 * index + 2,result);
}
}
中序遍历
中序遍历的顺序是:遍历左子树 --> 访问根节点 --> 遍历右子树。下图展示了中序遍历的过程。
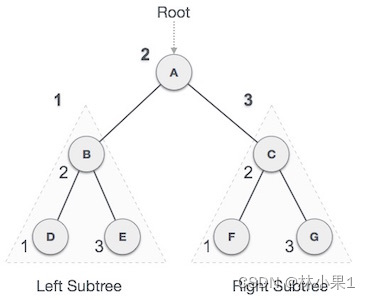
我们使用 infixOrder 方法来实现中序遍历。该方法接受一个索引和一个结果列表作为参数,然后将遍历的结果添加到结果列表中。
public void infixOrder(int index, List<E> result){
if(2 * index + 1 < arr.length){
infixOrder(2 * index + 1,result);
}
result.add(arr[index]);
if(2 * index + 2 < arr.length){
infixOrder(2 * index + 2,result);
}
}
后序遍历
后序遍历的顺序是:遍历左子树 --> 遍历右子树 --> 访问根节点。下图展示了后序遍历的过程。
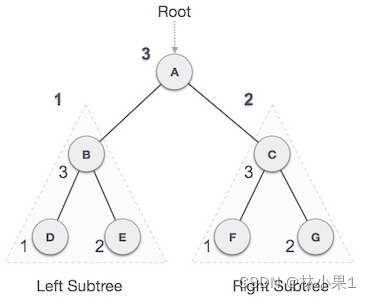
我们使用 postOrder 方法来实现后序遍历。该方法接受一个索引和一个结果列表作为参数,然后将遍历的结果添加到结果列表中。
public void postOrder(int index, List<E> result){
if(2 * index + 1 < arr.length){
postOrder(2 * index + 1,result);
}
if(2 * index + 2 < arr.length){
postOrder(2 * index + 2,result);
}
result.add(arr[index]);
}
文章来源:https://blog.csdn.net/weixin_74144099/article/details/135609836
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!