12- OpenCV：算子(Sobel和Laplance) 详解

目录

一、Sobel算子

1、卷积应用-图像边缘提取

2、Sobel算子（索贝尔算子）

3、相关的API（代码例子）

二、Laplance算子

1、理论

2、API使用（代码例子）

---

一、Sobel算子

1、卷积应用-图像边缘提取

?????????在这个红点变化最大，变化率很高的，梯度也是最陡。变化率做成一根曲线，所以变化率最大的就在顶点。

（1）边缘是什么 ：是像素值发生跃迁的地方，是图像的显著特征之一，在图像特征提取、对象检测、模式识别等方面都有重要的作用。

（2）如何捕捉/提取边缘 – 对图像求它的一阶导数 ?? ? ?

????????????????delta = ?f(x) – f(x-1), delta越大，说明像素在X方向变化越大，边缘信号越强，

（3）用Sobel算子就好！卷积操作！

2、Sobel算子（索贝尔算子）

（1）是离散微分算子（discrete differentiation operator），用来计算图像灰度的近似梯度；

（2）Soble算子功能集合高斯平滑和微分求导；

（3）又被称为一阶微分算子，求导算子，在水平和垂直两个方向上求导，得到图像X方法与Y方向梯度图像；

（4）求取导数的近似值，kernel=3时不是很准确，OpenCV使用改进版本Scharr函数，算子如下：放大了权重，差异性更加大了，不过也更加准确些。

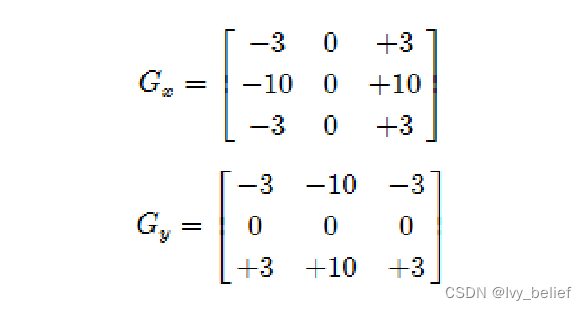
3、相关的API（代码例子）

（1）cv_Sobel函数原型

cv::Sobel (

InputArray Src // 输入图像

OutputArray dst// 输出图像，大小与输入图像一致

int depth // 输出图像深度.

int dx. ?// X方向，几阶导数

int dy // Y方向，几阶导数.

int ksize, SOBEL算子kernel大小，必须是奇数，1、3、5、7，一般是3

double scale ?= 1

double delta = 0

int borderType = BORDER_DEFAULT

)

（2）cv::Scharr

cv::Scharr (

InputArray Src // 输入图像

OutputArray dst// 输出图像，大小与输入图像一致

int depth // 输出图像深度.

int dx. ?// X方向，几阶导数

int dy // Y方向，几阶导数.

double scale ?= 1

double delta = 0

int borderType = BORDER_DEFAULT

)

（3）其他的API

— GaussianBlur( src, dst, Size(3,3), 0, 0, BORDER_DEFAULT );

— cvtColor( src, ?gray, COLOR_RGB2GRAY );

— addWeighted( A, 0.5,B, 0.5, 0, AB); convertScaleAbs(A, B)// 计算图像A的像素绝对值，输出到图像B

（4）代码演示

图像处理流程：

-高斯平滑（高斯模糊）GaussianBlur( )

-转灰度

-求梯度X和Y：做Sobel索贝尔计算

-得到振幅图像

#include <opencv2/opencv.hpp>
#include <iostream>
#include <math.h>

using namespace cv;
int main(int argc, char** argv) {
	Mat src, dst;
	src = imread("test.jpg");
	if (!src.data) {
		printf("could not load image...\n");
		return -1;
	}

	char INPUT_TITLE[] = "input image";
	char OUTPUT_TITLE[] = "sobel-demo";
	namedWindow(INPUT_TITLE, CV_WINDOW_AUTOSIZE);
	namedWindow(OUTPUT_TITLE, CV_WINDOW_AUTOSIZE);
	imshow(INPUT_TITLE, src);

	Mat gray_src;
	GaussianBlur(src, dst, Size(3, 3), 0, 0);
	cvtColor(dst, gray_src, CV_BGR2GRAY);
	imshow("gray image", gray_src);

	Mat xgrad, ygrad;
	Scharr(gray_src, xgrad, CV_16S, 1, 0);
	Scharr(gray_src, ygrad, CV_16S, 0, 1);

	// Sobel(gray_src, xgrad, CV_16S, 1, 0, 3);
	// Sobel(gray_src, ygrad, CV_16S, 0, 1, 3);

    // 转为绝对值
	convertScaleAbs(xgrad, xgrad);
	convertScaleAbs(ygrad, ygrad);
	imshow("xgrad", xgrad);
	imshow("ygrad", ygrad);

	Mat xygrad = Mat(xgrad.size(), xgrad.type());
	printf("type : %d\n", xgrad.type());
	int width = xgrad.cols;
	int height = ygrad.rows;
	for (int row = 0; row < height; row++) {
		for (int col = 0; col < width; col++) {
			int xg = xgrad.at<uchar>(row, col);
			int yg = ygrad.at<uchar>(row, col);
			int xy = xg + yg;
			xygrad.at<uchar>(row, col) = saturate_cast<uchar>(xy);
		}
	}
	//addWeighted(xgrad, 0.5, ygrad, 0.5, 0, xygrad);
	imshow(OUTPUT_TITLE, xygrad);

	waitKey(0);
	return 0;
}

效果展示：

二、Laplance算子

1、理论

解释：在二阶导数的时候，最大变化处的值为零即边缘是零值。通过二阶 导数计算，依据此理论我们可以计算图像二阶导数，提取边缘。

实际上就是：拉普拉斯算子操作（Laplance operator）-> cv::Laplance

2、API使用（代码例子）

（1）cv::Laplacian原型：

Laplacian(

InputArray src,

OutputArray dst,

int depth, //深度CV_16S

int kisze, // 3

double scale = 1,

double delta =0.0,

int borderType = 4

)

（2）代码演示

图像处理流程：

- 高斯模糊 – 去噪声GaussianBlur()

- 转换为灰度图像cvtColor()

- 拉普拉斯 – 二阶导数计算Laplacian()

-取绝对值convertScaleAbs()

-显示结果

#include <opencv2/opencv.hpp>
#include <iostream>
#include <math.h>

using namespace cv;
int main(int argc, char** argv) {
	Mat src, dst;
	src = imread("test.jpg");
	if (!src.data) {
		printf("could not load image");
	}
	char input_title[] = "input image";
	char output_title[] = "Laplaiance Result";
	namedWindow(input_title, CV_WINDOW_AUTOSIZE);
	imshow(input_title, src);

	Mat gray_src, edge_image;
	GaussianBlur(src, dst, Size(3, 3), 0, 0);
	cvtColor(dst, gray_src, CV_BGR2GRAY);

	Laplacian(gray_src, edge_image, CV_16S, 3);
	convertScaleAbs(edge_image, edge_image);

    // 边缘处理
	threshold(edge_image, edge_image, 0, 255, THRESH_OTSU | THRESH_BINARY);
	namedWindow(output_title, CV_WINDOW_AUTOSIZE);
	imshow(output_title, edge_image);

	waitKey(0);
	return 0;
}

效果展示：