最优化考试之黄金分割法

前言

最近要考最优化了，感觉时间有点赶，所以就直接学了解题方法，没去学习具体的原理了。

一、黄金分割法

1.解题条件

一般来说，题目会给出以下初始条件

1. 条件函数f(x)
2. 起始区间 [a0,b0]
3. 精度要求L

2.解题形式

先看下表格形式，我们解题就是在下列表格内不断迭代直至|a-b|<=L

迭代次数	a	b	x1	x2	f(x1)	f(x2)	|a-b|

1. a、b代表每次迭代时的左右区间;
2. x1、x2分别代表每次迭代的左右试点（这部分计算就会用到黄金分割）;
3. f(x1)、f(x2)分别代表左右试点的函数值，根据二者大小决定下一次迭代更新左端点a还是右端点b;
4. |a-b|代表达到的结果精度，当它小于等于L时迭代结束。

3.解题过程

1. 第一次迭代将初始点a0、a0作为a、b值；
2. 计算当前a、b绝对值之差，如果小于等于精度范围L，停止迭代；
3. 计算左试点x1，公式如下
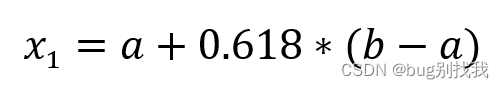
4. 计算右试点x2，公式如下
   
   5.分别计算f(x1)、f(x2)值，比较二者大小；
   若f(x1)大于f(x2)，则更新下一次迭代的a为x1;
   若f(x2)大于f(x1)，则更新下一次迭代的b为x2;
   总而言之，就是哪边试点的函数值大下一次就更新哪边的端点。
   6.迭代次数加一，回到第2步。

4.案例

这是网上找的一道题目，字写的丑就不丢人了，这道题没有具体说明它的精度范围，我就自行定义了精度范围为0.05，大家可以根据第三节的过程来跟着运算一下，最终写在纸张上的形式应该和下面代码结果截图的形式基本一样。

二、K-T点求解

1.问题形式

直接拿道题来举例子，以下是我们要求的目标函数f(x)，我们希望找到它的最小值。

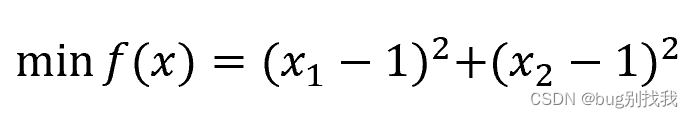
而它的约束如下，约束有等式也会有不等式，这里等式不用多说，直接用即可，主要是不等式的处理，我们要处理成统一的约束函数形式，这里的约束函数g(x)都小于等于0。

2.转化形式

对约束不等式g(x)进行合理的转化

min f(X)	max f(X)
g(X)<=0	g(X)>=0

3.解题过程

1. 构建拉格朗日函数，将目标函数放进去，再将约束函数乘以对应的拉格朗日乘子λ放入；
   
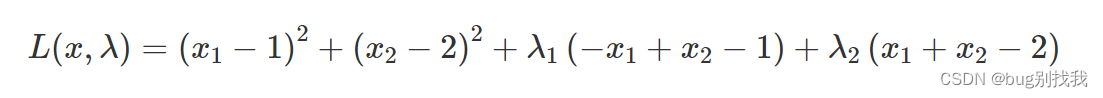
2. K_T条件约束如下
   
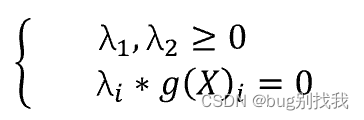
   3.对拉格朗日函数L求参数x1、x2的偏导，如下所示
   
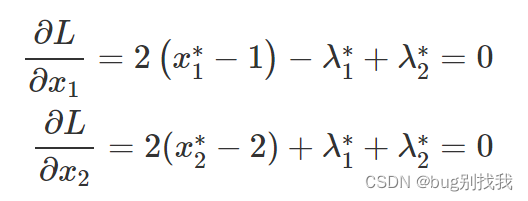
3. 这里就需要讨论一下λ _2是否等于0的情况了；
4. 当λ _2等于0时，算得x1、x2结果为4、-1,不满足约束x1+x2<=2;
5. 当λ_2不等于0，即x1+x2=2,算得x1、x2结果为1/2、3/2，约束条件均成立；
6. 因此x=(1/2,3/2)为最优解，f=1/2是最小值。