SICP : The Elements of Programming，Exercise 1.4、1.5、1.6、1.7、1.8

Exercise 1.4

function plus(a, b)
{
    return a + b;
}

function minus(a, b)
{
    return a - b;
}

function a_plus_abs_b(a, b)
{
    return (b >= 0 ? plus : minus) (a,b);
}

a_plus_abs_b(3,-4);

// out put 7

a_plus_abs_b(-7 , -3);

// out put -4

Exercise 1.5

function p()
{
    return p();
}

function test(x, y)
{
    return x === 0 ? 0 : y;
}

test(0,p());

Error: Line 11: The function p has encountered an infinite loop. It has no base case.，这题没搞懂！！！懂的同学可以评论里给大家分享这美好的知识，谢谢。

Example: Square Roots by Newton’s Method

function sqrt_iter(guess,x)
{
    return is_good_enough(guess,x)
    ? guess
    :sqrt_iter(improve(guess,x),x);
}

function improve(guess,x)
{
    return average(guess,x / guess);
}

function average(x,y)
{
    return (x + y) / 2;
}

function is_good_enough(guess,x)
{
    return abs(square(guess) - x) < 0.001;
}

function sqrt(x)
{
    return sqrt_iter(1,x);
}

function abs(x)
{
    return x > 0 ? x : -x;
}

function square(x)
{
    return x * x;
}

sqrt(9);

sqrt(100 + 37);

sqrt(sqrt(2) + sqrt(3));

square(sqrt(1000));

1000.000369924366

Exercise 1.6

function conditional(predicate,then_clause,else_clause)
{
    return predicate ? then_clause : else_clause;
}

conditional(2 === 3,0, 5);

conditional(1 === 1,0,5);

function improve(guess,x)
{
    return average(guess,x / guess);
}

function average(x,y)
{
    return (x + y) / 2;
}

function is_good_enough(guess,x)
{
    return abs(square(guess) - x) < 0.001;
}

function sqrt(x)
{
    return sqrt_iter(1,x);
}

function abs(x)
{
    return x > 0 ? x : -x;
}

function square(x)
{
    return x * x;
}

function sqrt_iter(guess,x)
{
    return conditional(is_good_enough(guess,x),
    guess,
    sqrt_iter(improve(guess,x),
    x));
}

sqrt_iter(1,3);

Line 49: The function sqrt_iter has encountered an infinite loop. It has the infinite cycle: (guess: 1.7320508075688772), (x: 3) -> (guess: 1.7320508075688772), (x: 3).
由于控制精度太小，所以出现无穷递归的逻辑，其实递归真的强大，递归可以实现遍历，类似for和while的逻辑处理用递归照样可以实现。

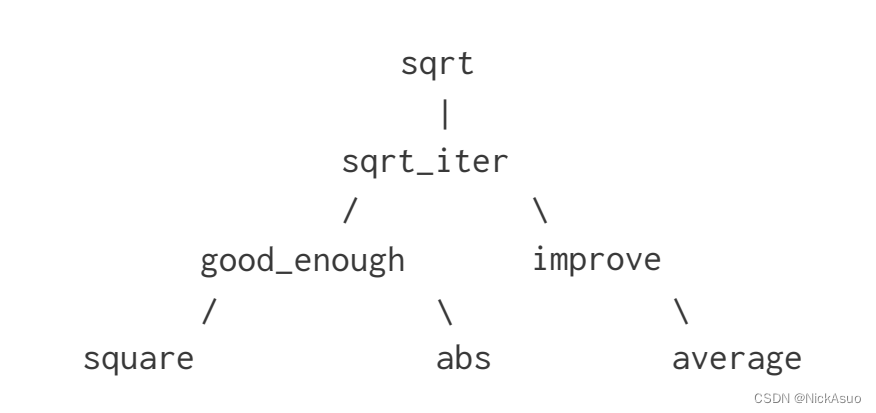
把一个计算机功能分解成多个更细粒度的子功能，是一种处理计算机问题非常好的思路

Exercise 1.8

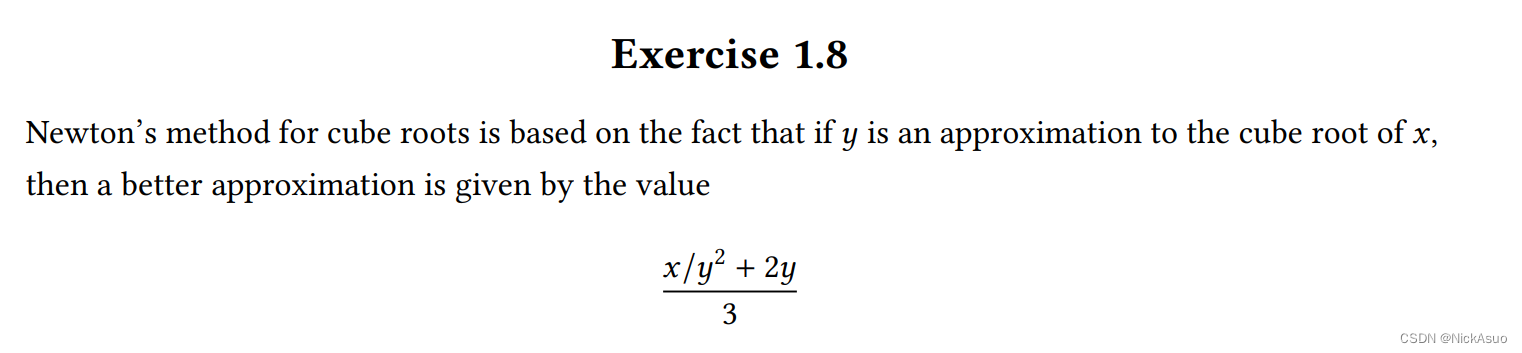
什么是扩展性极强的编程语言？，在写功能的时候，可以缺什么就去创造什么，而且创造的很便利，加 减 乘 除的接口可以作为数据输入，也可以成为操作接口，所以带来了极大便利。

function div(a,b)
{
    return a / b;
}

function multi(a,b)
{
    return a * b;
}

function add(a,b)
{
     return a + b;
}

function improve(guess,x)
{
    return div(add(div(x,square(guess)),multi(2,guess)),3);
}

function average(x,y)
{
    return (x + y) / 2;
}

function is_good_enough(guess,x)
{
    return abs(square(guess) - x) < 0.5;
}

function sqrt(x)
{
    return sqrt_iter(1,x);
}

function abs(x)
{
    return x > 0 ? x : -x;
}

function square(x)
{
    return x * x;
}

function sqrt_iter(guess,x)
{
    return is_good_enough(guess,x)?
    guess
    :
    sqrt_iter(improve(guess,x),
    x);
}

sqrt_iter(1,3);

1.6666666666666667

Functions as Black-Box Abstractions

// So a function should be able to suppress detail.
// 计算机功能接口应该设计成黑盒接口，隐藏其内部实现，不需要知道接口内部具体实现
function square(x)
{
    return x * x;
}

function square(x)
{
    return math_exp(double(math_log(x)));
}

function double(x)
{
    return x + x;
}