力扣算法-Day17

15. 三数之和

给你一个整数数组?nums?，判断是否存在三元组?[nums[i], nums[j], nums[k]]?满足?i != j、i != k?且?j != k?，同时还满足?nums[i] + nums[j] + nums[k] == 0?。请?

你返回所有和为?0?且不重复的三元组。

注意：答案中不可以包含重复的三元组。

思路：

双指针：首先要将nums数组进行排序。原因有以下几点：

1. 对比于两数之和，本题没有让我们返回数组的下标，如果返回下标的话，则不能够进行排序。
2. 排好序后方便我们对元素范围的收缩。

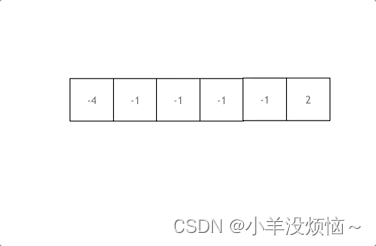
如下图：拿这个nums数组来举例，首先将数组排序，然后有一层for循环，i从下标0的地方开始，同时定一个下标left 定义在i+1的位置上，定义下标right 在数组结尾的位置上。

依然还是在数组中找到 abc 使得a + b +c =0，我们这里相当于 a = nums[i]，b = nums[left]，c = nums[right]。

接下来如何移动left 和right呢， 如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了，因为数组是排序后了，所以right下标就应该向左移动，这样才能让三数之和小一些。

如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了，left 就向右移动，才能让三数之和大一些，直到left与right相遇为止。

整体寻找三数之和的代码比较容易的，最重要的还是去重的操作。

首先是对a的去重：去重的话是与前一个比较呢还是与后一个比较？

例如{-1, -1 ,-1，2} 这组数据，当遍历到第一个-1 的时候，并且收集一个三元组之后发现一个也是-1，那这组数据就pass了。

????????????????if (i > 0 && nums[i] == nums[i - 1]) {
????????????????? ? continue;
????????????????}

其次就是b与c的去重：

当我们收集到一个三元组后，发现下一个元素和当前指向相同，则进行移动。

? ? ? ? ? ? ? ? while(right > left && nums[right] == nums[right - 1])
? ? ? ? ? ? ? ? ? ? right--;
? ? ? ? ? ? ? ? while(left < right && nums[left] == nums[left + 1])
? ? ? ? ? ? ? ? ? ? left++;

实现代码如下：

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
 int partition (int* a,int low, int high) {
	int key= a[low];
	while (low < high) {
		while (low < high && a[high] >= key) 
			--high;
		a[low] = a[high];
		while (low < high && a[low] <= key)
			++low;
		a[high] = a[low];
	}
	a[low] = key;
	return low;
}
void QSort (int* a,int low, int high) {
	if (low<high) {
		int pivotloc = partition(a,low,high);
		QSort(a,low,pivotloc-1);
		QSort(a,pivotloc+1,high);
	}
}

int** threeSum(int* nums, int numsSize, int* returnSize, int** returnColumnSizes) {
    //快速排序
    QSort(nums,0,numsSize-1);
    //开辟数组空间
    int **ans = (int **)malloc(sizeof(int*)*1000);
    int ansTop = 0;
    for (int i = 0; i < numsSize - 1; i++) {
        if (nums[i] > 0) break;
        //对a去重
        if (i > 0 && nums[i] == nums[i-1]) continue;
        //定义左右指针
        int left = i+1;
        int right = numsSize-1;
        //当右指针大于做指针时进行循环
        while (right > left) {
             //求出三数之和
            int sum = nums[right] + nums[left] + nums[i];
            //若和小于0，则左指针+1（因为左指针右边的数比当前所指元素大）
            if(sum < 0)
                left++;
            //若和大于0，则将右指针-1
            else if(sum > 0)
                right--;
            //若和等于0
            else {
                //存储
                int* arr = (int*)malloc(sizeof(int)*3);
                arr[0] = nums[i];
                arr[1] = nums[left];
                arr[2] = nums[right];
                ans[ansTop++] = arr;
                //去重
                while(right > left && nums[right] == nums[right - 1])
                    right--;
                while(left < right && nums[left] == nums[left + 1])
                    left++;
                //更新左右指针
                left++;
                right--;
            }
        }
    }
    //返回数组大小
    *returnSize = ansTop;
    *returnColumnSizes = (int*)malloc(sizeof(int)*ansTop);
    for (int z = 0; z < ansTop; z++) {
        (*returnColumnSizes)[z] = 3;
    }
    return ans;
}

?前段时间因为有点事情，从今天开始将继续同各位一起努力！！

?这一期专栏记录将我每天的刷题，希望各位的监督，也希望和各位共勉。

追光的人，终会光芒万丈！！