C++力扣题目46--全排列

46.全排列

力扣题目链接(opens new window)

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

• 输入: [1,2,3]
• 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]

#思路

此时我们已经学习了77.组合问题?(opens new window)、?131.分割回文串?(opens new window)和78.子集问题?(opens new window)，接下来看一看排列问题。

相信这个排列问题就算是让你用for循环暴力把结果搜索出来，这个暴力也不是很好写。

所以正如我们在关于回溯算法，你该了解这些！?(opens new window)所讲的为什么回溯法是暴力搜索，效率这么低，还要用它？

因为一些问题能暴力搜出来就已经很不错了！

我以[1,2,3]为例，抽象成树形结构如下：

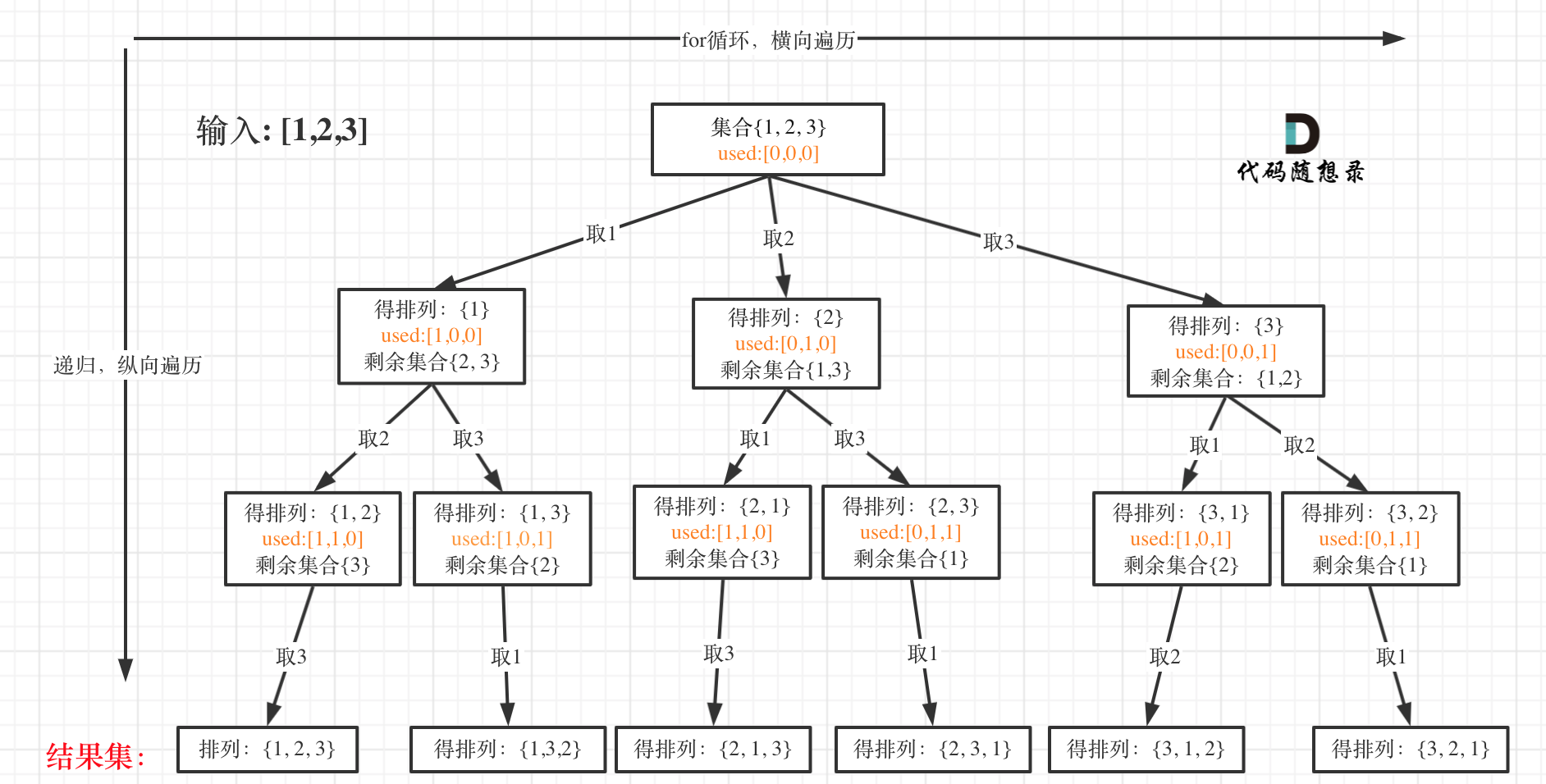
#回溯三部曲

• 递归函数参数

首先排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。

可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。

但排列问题需要一个used数组，标记已经选择的元素，如图橘黄色部分所示:

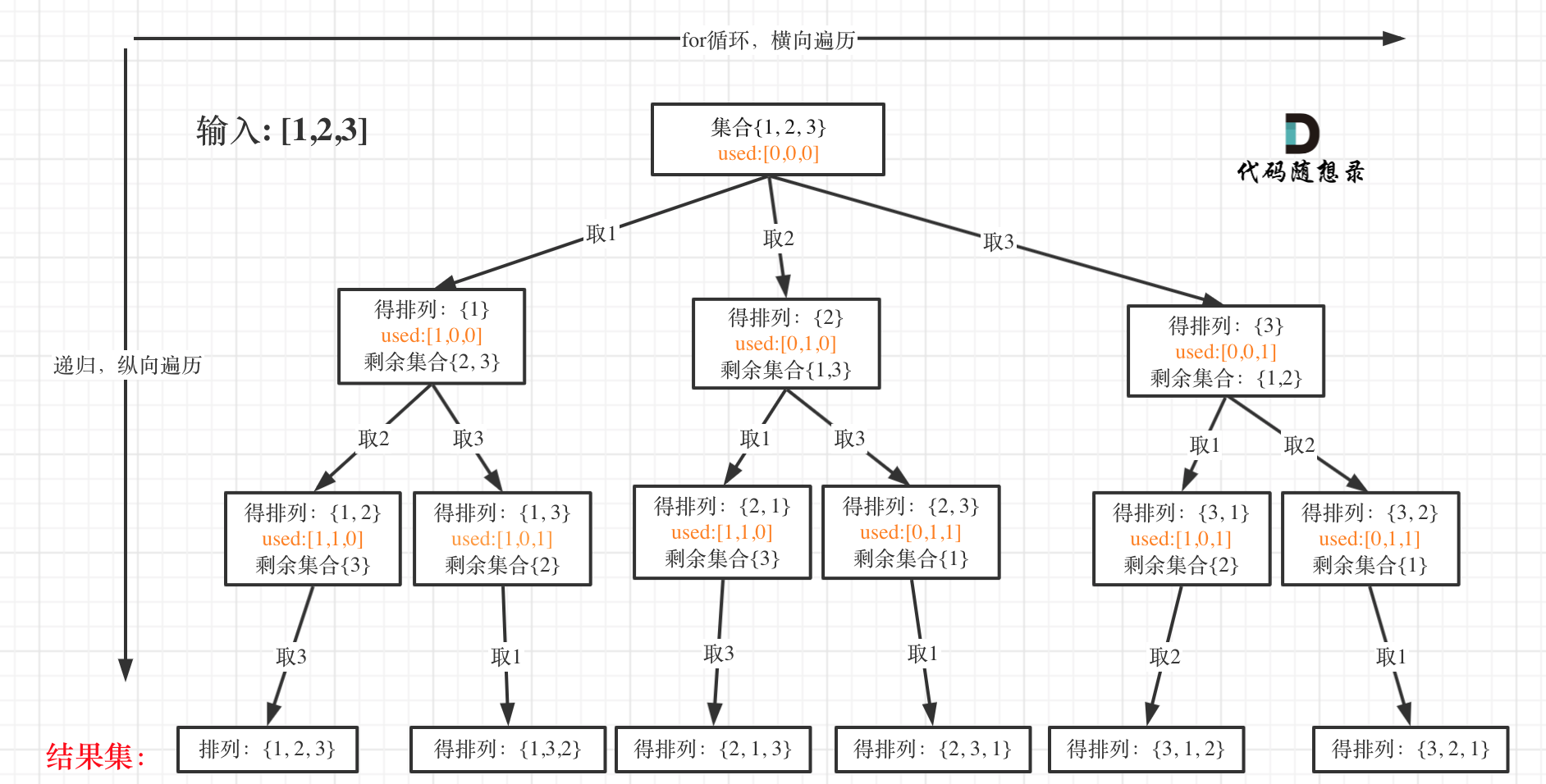
代码如下：

vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used)

• 递归终止条件

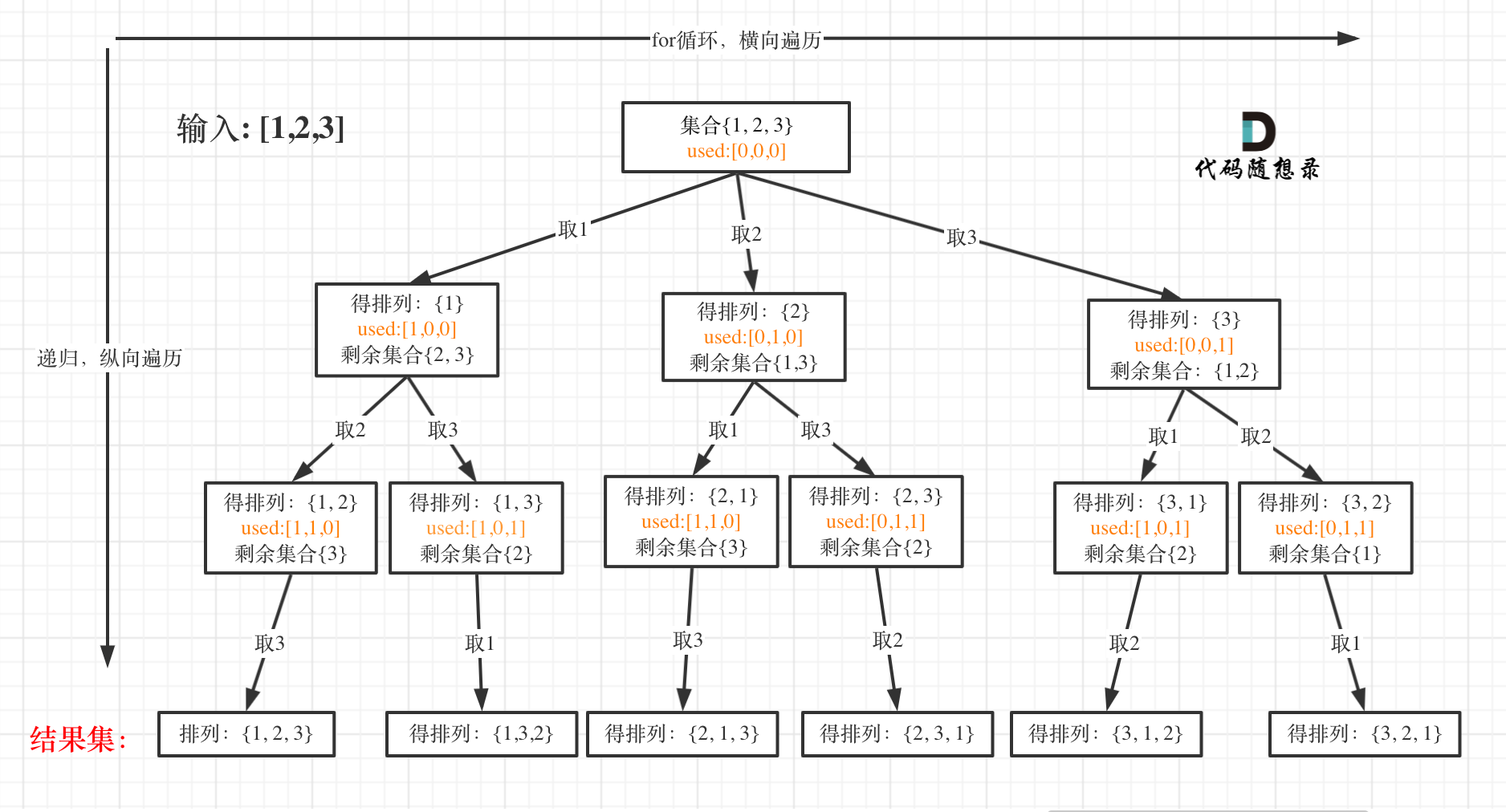
可以看出叶子节点，就是收割结果的地方。

那么什么时候，算是到达叶子节点呢？

当收集元素的数组path的大小达到和nums数组一样大的时候，说明找到了一个全排列，也表示到达了叶子节点。

代码如下：

// 此时说明找到了一组
if (path.size() == nums.size()) {
    result.push_back(path);
    return;
}

• 单层搜索的逻辑

这里和77.组合问题?(opens new window)、131.切割问题?(opens new window)和78.子集问题?(opens new window)最大的不同就是for循环里不用startIndex了。

因为排列问题，每次都要从头开始搜索，例如元素1在[1,2]中已经使用过了，但是在[2,1]中还要再使用一次1。

而used数组，其实就是记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次。

代码如下：

for (int i = 0; i < nums.size(); i++) {
    if (used[i] == true) continue; // path里已经收录的元素，直接跳过
    used[i] = true;
    path.push_back(nums[i]);
    backtracking(nums, used);
    path.pop_back();
    used[i] = false;
}

整体C++代码如下：

class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking (vector<int>& nums, vector<bool>& used) {
        // 此时说明找到了一组
        if (path.size() == nums.size()) {
            result.push_back(path);
            return;
        }
        for (int i = 0; i < nums.size(); i++) {
            if (used[i] == true) continue; // path里已经收录的元素，直接跳过
            used[i] = true;
            path.push_back(nums[i]);
            backtracking(nums, used);
            path.pop_back();
            used[i] = false;
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        result.clear();
        path.clear();
        vector<bool> used(nums.size(), false);
        backtracking(nums, used);
        return result;
    }
};

• 时间复杂度: O(n!)
• 空间复杂度: O(n)

#总结

大家此时可以感受出排列问题的不同：

• 每层都是从0开始搜索而不是startIndex
• 需要used数组记录path里都放了哪些元素了

排列问题是回溯算法解决的经典题目，大家可以好好体会体会