算法练习——盛最多水的容器

题目描述：

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明： 你不能倾斜容器。

示例 1：

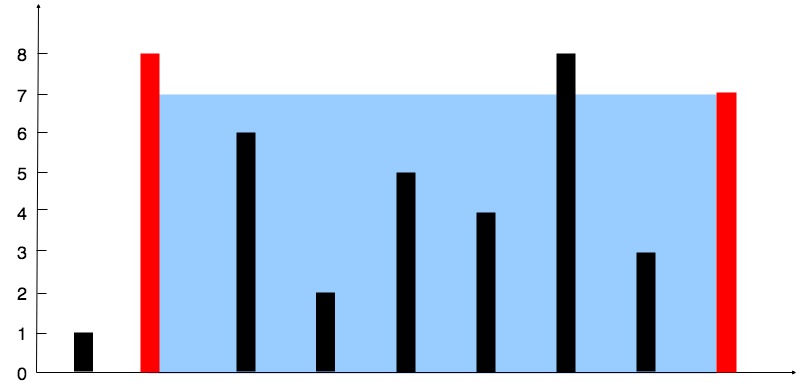
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

通过代码：

class Solution {
    public int maxArea(int[] height) {
        int left = 0;
        int right = height.length - 1;
        //  返回的最大值
        int result = 0;
        while( left < right ){
            //  记录此时组成的容积
            int volume = (height[left]<height[right]?height[left]:height[right]) * (right - left);
            if(volume > result) result = volume;
            if (height[left] <= height[right]) {
                ++left;
            }else{
                --right;
            }
        }
        return result;
    }
}

解析：

首先我们声明两个指针 left, right ，分别指向的水槽板两侧，高度为height[left], height[right]。

由于可容纳水的高度由两板中的 短板 决定，因此可得 此状态下水槽面积公式为 ：

$volume(i,j)=min(height[left],height[right])\times (right?left)$

在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽宽度 $(right?left)$ 变短：

若向内 移动短板 ，水槽的短板 $min(height[left],height[right])$ 可能 变大，因此下个水槽的面积 可能增大 。
若向内 移动长板 ，水槽的短板 $min(height[left],height[right])$ 不变 或 变小 ，因此下个水槽的面积 一定变小 。

因此，初始化双指针分列水槽左右两端，循环每轮将 短板 向内移动一格，并更新面积最大值result。当两指针相遇时结束循环，此时存储的 result 即为获得最大面积。

复杂度分析：

时间复杂度：$O(n)$；双指针遍历为 n == height.length

空间复杂度：$O(1)$.