【数据结构】查找与排序

发布时间：2023年12月25日

要查询信息，涉及两个问题：

在哪里查？——查找表

怎么查？——查找方法

一.查找

1.查找表的定义：

查找表是由同类型的数据元素构成的集合

2.对查找表的基本操作：

1）查询某个数据元素是否在查找表中

2）检索某个数据元素的各种属性

3）在查找表中插入一个数据元素

4）从查找表中删除某个元素

3.查找表的分类：

静态查找表：

仅作查询和检索操作的查找表

动态查找表：

可以进行“插入”和“删除”操作

4.关键字：

关键字：是数据元素中某个数据项的值，用以标识一个数据元素。

主关键字：若关键字能标识唯一的一个数据元素

次关键字：若关键字能标识若干个数据元素

5.查找：

根据给定的某个值，在查找表中确定一个其关键字等于给定值的数据元素。

6.查找方法评价：

算法本身的时间复杂度
临时变量占用存储空间的多少
平均查找长度ASL（Average Search Length）

对于含有n个记录的表， $ASL=\sum_{i=1}^{n}p_ic_i$

其中， $p_i$ 为查找表中第i个元素的概率， $\sum_{i=1}^{n}p_i=1$

$c_i$ 为找到表中第i个元素所需要比较的次数

7. 顺序表的查找：

7.1 基本思想：

从表中指定位置的记录开始，沿着某个方向将记录的关键字与给定值相比较，若某个记录的关键字与给定值相同，则查找成功。

反之，若找完整个顺序表，都没有与给定关键字值相同的记录，则查找失败。

7.2 顺序查找的性能分析：

查找第n个元素：1次

查找第n-1个元素：2次

...

查找第1个元素：n次

查找第i个元素：n+1-i次

查找失败：n+1次

空间复杂度：

需要一个辅助空间R[0]

时间复杂度：

$ASL=\sum_{i=1}^{n}p_ic_i$ ????????? $c_i=n-i+1$

等概率情况下： $ASL=\frac{n+1}{2}$

平均情况： $O(n)$

优点：算法简单，适用面广

缺点：平均查找长度较大

?8.折半查找

8.1 基本思想：

查找过程：每次将待查记录所在区间缩小一半。

适用条件：采用顺序存储的有序表

8.2 伪代码：

设表长为n，low、high和mid分别指向待查元素所在区间的上界、下界和中点，k为给定值。

初始时，令low=0，high=n-1，mid=(high+low)/2。

让k与mid指向的记录比较

若k==r[mid].key 查找成功
若k<r[mid].key 则high=mid-1
若k>r[mid].key 则low=mid+1

重复上述操作，直至low>high为止，查找失败。

int biserach(int r[],int n,int k){
    int low=0,high=n-1,mid=0;
    while(low<=high){
        mid=(low+high)/2;
        if(r[mid]==k){
            break;
        }
        else if(r[mid]>k){
            high=mid-1;
        }
        else{
            low=mid+1;
        }
    }
    if(low>high){
        return -1;
    }
    else{
        return mid;
    }
}

8.3 算法性能分析：

判定树：描述查找过程的二叉树

有n个结点的判定树的层次数为 $\lfloor log_2n\rfloor +1$

折半查找在查找过程中进行的比较次数最多不超过其判定树的深度。

折半查找的ASL：

设表长为 $2^h-1$ , $h=log_2{(n+1)}$ ,即判定树为深度为h的满二叉树

设表中每个记录的查找概率相等

$ASL=\sum_{i=1}^{n}p_ic_i=\frac{1}{n} \sum_{i=1}^{n}c_i=\frac{1}{n}\sum_{j=1}^{h}j*2^{j-1}=\frac{n+1}{n}log_2{(n+1)}-1\approx log_2(n+1)-1$ ?

8.4 折半查找的特点：

1）查找效率高

2）平均查找性能和最坏性能相当接近

3）要求查找表为有序表

4）只适用于顺序存储结构

9.索引表查找

9.1 索引表的构建

数据分块：

按关键字分成若干块 $R_1,R_2,...,R_L,R_k<R_{k+1}$ ，达到分块有序。

建索引项：

每一个块建立一个索引项，每个索引项包含最大关键字项，块的起始地址。

组成索引表：

所有索引项组成索引表

9.2 索引表的查找：

索引表内查找：确定关键字所在区块。

查找表内查找：查找表的某个块内查找

9.3 索引表查找的代码实现：

typedef struct{
    int key;
    int link;
}SD;
typedef struct{
    int key;
    float info;
}JD;
int block_search(JD r[],SD nd[],int b,int k,int n){//n个记录分成b块
    int i=0,j;
    while(k>nd[i].key&&i<b){
        i++;
    }
    if(i>=b){
        cout<<"not found"<<endl;
        return -1;
    }
    else{
        //在块内顺序查找
        j=nd[i].link;
        while(j<n&&k!=r[j].key){
            j++;
        }
        if(k!=r[j].key){
            cout<<"not found"<<endl;
            return -1;
        }
        else{
            return j;
        }
    }
}

9.4 分块查找方法评价：

$ASL=L_b+L_w$ ?

若将表长为n的表平均分成b块，每块含有s个记录，并设表中每个记录的查找概率相等。

则有：

1）用顺序查找确定所在块：

$ASL=\frac{1}{b}\sum_{j=1}^bj+\frac{1}{s}\sum_{i=1}^si=\frac{b+1}{2}+\frac{s+1}{2}=\frac{1}{2}(\frac{n}{s}+s)+1$

2)用折半查找确定所在块：

$ASL\approx log_2(\frac{n}{s}+1)+\frac{s}{2}$

10.查找方法比较

	顺序查找	折半查找	索引查找
ASL	最大	最小	两者之间
表结构	有序表、无序表	有序表	分块有序表
存储结构	顺序存储、单链表	顺序存储	顺序存储、单链表

11.哈希表查找?

ASL=1的查找算法。

如果可以确定关键字与存储位置的对应关系，就有可能让ASL=1.

11.1 哈希查找的基本定义：

哈希函数：在记录的关键字与记录的存储地址之间建立的一种对应关系

哈希查找：又叫散列查找，利用哈希函数进行查找的过程。

哈希函数是一种映射，即从关键字空间到存储地址空间的一种映射。

哈希函数可以写成：

$H(k_i)=addr(k_i)$

11.2 冲突

哈希函数通常是一种压缩映射，所以冲突不可避免。

冲突发生后，应该有处理冲突的方法。

（1）直接定址法（线性函数）：

例如：H(key)=key-1948

?直接定址法所得地址集合与关键字集合大小相等，不会发生冲突。

?(2)数字分析法：

对关键字进行分析，取关键字的若干位或其组合作为哈希地址。

适用于关键字位数比哈希地址位数大，且可能出现的关键字事先知道的情况。

（3）平方取中法：

取关键字平方后的中间几位作为哈希地址

为什么要取关键字的平方值？

扩大差别?
均衡贡献

（4）折叠法：

将关键字分割为位数相同的几部分，然后取这几部分的叠加和（舍去进位）作哈希地址。

适用于关键字位数很多，且每一位上数字分布大致均匀的情况

例如：关键字为 04 4220 5864 哈希地址位数为4

移位叠加：? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 间界叠加：

5? ? ? ? 8? ? ? ? 6? ? ? ? 4? ? ? ? ? ? ? ? ? ? ? ? 5? ? ? ? 8? ? ? ? 6? ? ? ? 4

4? ? ? ? 2? ? ? ? 2? ? ? ? 0? ? ? ? ? ? ? ? ? ? ? ? 0? ? ? ? 2? ? ? ? 2? ? ? ? 4

0? ? ? ? 0? ? ? ? 0? ? ? ? 4? ? ? ? ? ? ? ? ? ? ? ? 0? ? ? ? 0? ? ? ? 0? ? ? ? 4

---------------------------------------------------------------------------

（5）除留余数法：

H(key)=key MOD p,p<=m,m为hash表长。

p选取不好，容易产生同义词，通常选取一个质数。

（6）伪随机数法

取关键字的随机函数作哈希地址值，即：H(key)=random(key)

适用于关键字长度不等的情况。

11.3 选取哈希函数需要考虑的因素：

1）计算哈希函数所需的时间

2）关键字长度

3）哈希表长度

4）关键字分布情况

5）记录的查找频率

11.4 冲突处理

为出现哈希地址冲突的关键字寻找下一个新的哈希地址。

（1）开放定址法：

当冲突发生时，形成一个探查序列，沿着此序列逐个地址探查，直到找到一颗空位置，将发生冲突的记录放入该地址中，即 $H_i=(H(key)+di)MOD \quad m$

m 哈希表表长，di 增量序列。

增量序列分类：

线性探测再散列?di=1,2,3,...,m-1

平方探测再散列? $di=1^2,-1^2,2^2,-2^2,...,\pm k^2(k\leq m/2)$

伪随机探测再散列 di=伪随机数序列

例：

（2）再哈希法：

构造若干个哈希函数，当发生冲突时，计算下一个哈希地址。

（3）链地址法：

将所有关键字为同义词的记录存储在一个单链表中，并用一位数组存放头指针。

（4）公共溢出区法

假设某哈希函数的值域为[o,m-1]

向量HashTable[0,m-1]为基本表，每个分量存放一个记录，另设一个向量OverTable[0,v]为溢出表。将与基本表中的关键字发生冲突的所有记录都填入溢出表中。

11.5 例题分析

已知一组关键字（19，14，23，1，68，20，84，27，55，11，10，79）

哈希函数为H(key)=key MOD 13 ，哈希表长为16，设每个记录的查找概率相等。

1）线性探测再散列处理冲突

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
	14	1	68	27	55	19	20	84	79	23	11	10

1 1 1 2 1 1 3 4 3 1 3 9

ASL=30/12=2.5

2）链地址法处理冲突

ASL=（6*1+4*2+1*3+1*4）/12=1.75

11.6 哈希查找分析

哈希查找过程仍然是一个给定值与关键字进行比较的过程

评价哈希查找仍要用ASL

哈希查找过程与给定值进行关键字比较的次数取决于：

哈希函数
处理冲突的方法
哈希表的装载因子 $\alpha$

$\alpha =k/L$

k:表中填入的记录数

L:哈希表长度

二.排序

1.内部排序的方法：

内部排序的过程是一个逐步扩大有序区记录的过程

2.排序分为：

稳定排序
不稳定排序

3.直接插入排序（稳定）：

3.1 基本思想：

先将序列中第一个记录看成是一个有序子序列，然后从第二个记录开始，逐个进行插入，直至整个序列有序。整个排序过程为n-1躺插入。

3.2 具体例子：

i=1? ? ? ? 49 38 65 97 76 13 27

i=2? ? ? ? 38?49?65 97 76 13 27

i=3????????38?49?65 97 76 13 27

i=4????????38?49?65 97 76 13 27

i=5????????38?49?65 76 97 13 27

i=6? ? ? ? 13 38?49?65 97 76 27

i=7? ? ? ? 13 27 38?49?65 76 97

3.3 代码实现：

void insert_select(int r[],int n){
    int i,j,temp;
    for(i=1;i<n;i++){
        temp=r[i];
        j=i-1;
        while(temp<r[j]){
            r[j+1]=r[j];
            --j;
        }
        r[j+1]=temp;
    }
}

3.4 算法评价：

时间复杂度：

$O(n^2)$

空间复杂度：

$O(1 )$

4.折半插入排序（稳定）

4.1 基本思想：

用折半查找方法确定插入位置的排序

4.2 算法分析：

时间复杂度：

$O(n^2)$

空间复杂度：

$O(1 )$

5.希尔排序（缩小增量法）（非稳定）

5.1 基本思想：

希尔排序是对插入排序的改进。

(1) 插入排序对几乎已排好序的数据操作时，效率很高，可以达到线性排序的效率。?

(2) 插入排序在每次往前插入时只能将数据移动一位，效率比较低。

先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）。分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。

局部有序不能提高直接插入排序算法的时间性能

5.2 代码实现：

void shell_sort(int r[],int n){
    int di=n/2,i,j,temp;
    while(di>=1){
        for(i=di;i<n;i++){
            j=i-di;
            temp=r[i];
            while(temp>r[j]&&j>=0){
                r[j+di]=r[j];
                j-=di;
            }
            r[j+di]=temp;
        }
        di/=2;
    }
}

5.3 性能分析：

时间复杂度：

$O(nlog_2n)$

空间复杂度：

S(1)

6.冒泡排序（稳定）

6.1 基本思想：

两两比较相邻记录的关键码，如果反序则交换，直到没有反序的记录为止。

6.2 对冒泡排序的改进：

1）设变量exchange记载记录交换的位置。则一趟排序后，exchange记载的一定是这一趟排序中记录的最后一次交换的位置。且从此位置以后的记录均已有序。

2）设bound位置的记录是无序区的最后一个记录，则每趟冒泡排序的范围是r[0]~r[bound]。

在一趟排序后，从exchange位置之后的记录一定是有序的，所以bound=exchange。

3）令exchange初值为0，在以后的排序中，只要有记录交换，exchange的值就会大于0。则当exchange=0时，冒泡排序结束。

6.3 代码实现：

void buble_sort(int r[],int n){
    int exchange=n-1,bound,i,temp;
    while(exchange){
        bound=exchange;
        exchange=0;
        
        for(i=0;i<bound;i++){
            if(r[i]>r[i+1]){
                temp=r[i];
                r[i]=r[i+1];
                r[i+1]=temp;
                exchange=i;
            }
        }
        
    }
    
}

6.4 性能分析：

时间复杂度：

$O(n^2)$

空间复杂度：

$O(1 )$

7.快速排序

7.1 基本思想：

通过一趟排序将待排记录分隔成独立的两部分。其中一部分记录的关键码均比另一部分的关键码小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

首先选取一个轴值。通过一趟排序，将待排序记录分割成独立的两部分。前一部分记录的关键码均小于或等于轴值；后一部分记录的关键码均大于或等于轴值。然后分别对这两部分重复上述方法。

7.2 如何实现划分：

设待划分的序列是r[s]~r[t]。设参数i，j分别指向子序列左右两端的下标，s和t。令r[s]为轴值。

j从后向前扫描直到r[j]<r[i]，将r[j]移动到r[i]的位置，使关键码小的记录移动到前面。
i从前向后扫描直到r[i]>r[j]，将r[i]移动到r[j]的位置，使关键码大的记录移动到后面。
重复上述过程，直到i=j。

7.3 递归出口：

?若待排序序列中只有一个记录，则显然有序，否则进行一次划分后，再分别对所得的两个子序列进行快速排序。

7.4 代码实现：

int get_partition(int first,int end,int r[]){
    int i=first,j=end,temp;
    while(i<j){
        while(r[i]<=r[j]&&i<j){
            --j;
        }
        if(i<j){
            temp=r[j];
            r[j]=r[i];
            r[i]=temp;
            ++i;
        }
        while(r[i]<=r[j]&&i<j){
            ++i;
        }
        if(i<j){
            temp=r[j];
            r[j]=r[i];
            r[i]=temp;
            --j;
        }
    }
    return i;
}
void quick_sort(int r[],int first,int end){
    if(first<end){
        int pos=get_partition(first, end, r);
        quick_sort(r, first, pos-1);
        quick_sort(r, pos+1, end);
    }
}

7.5 性能分析：

时间复杂度与选取的轴值有关。

最好情况为：每次均选取到中间值作为轴值；最坏情况为：每次都选取到最大或最小元素最为轴值。

平均时间复杂度： $O(nlog_2n)$

最坏时间复杂度： $O(n^2)$

采用“三者取中”来确定轴值，即：第一个元素，最后一个元素，最中间的元素中的中间值作为划分元。

空间复杂度： $O(log_2n)$

8.选择排序

8.1 基本思想：

?每趟排序在当前待排序序列中选出关键码最小的记录，添加到有序序列中。

8.2 代码实现：

void select_sort(int r[],int n){
    int min,i,j,temp;
    for(i=0;i<n-1;i++){
        min=i;
        for(j=i+1;j<n;j++){
            if(r[j]<r[min]){
                min=j;
            }
        }
        if(min!=i){
            temp=r[min];
            r[min]=r[i];
            r[i]=temp;
        }
    }
}

8.3 性能分析：

时间复杂度:

$O(n^2)$

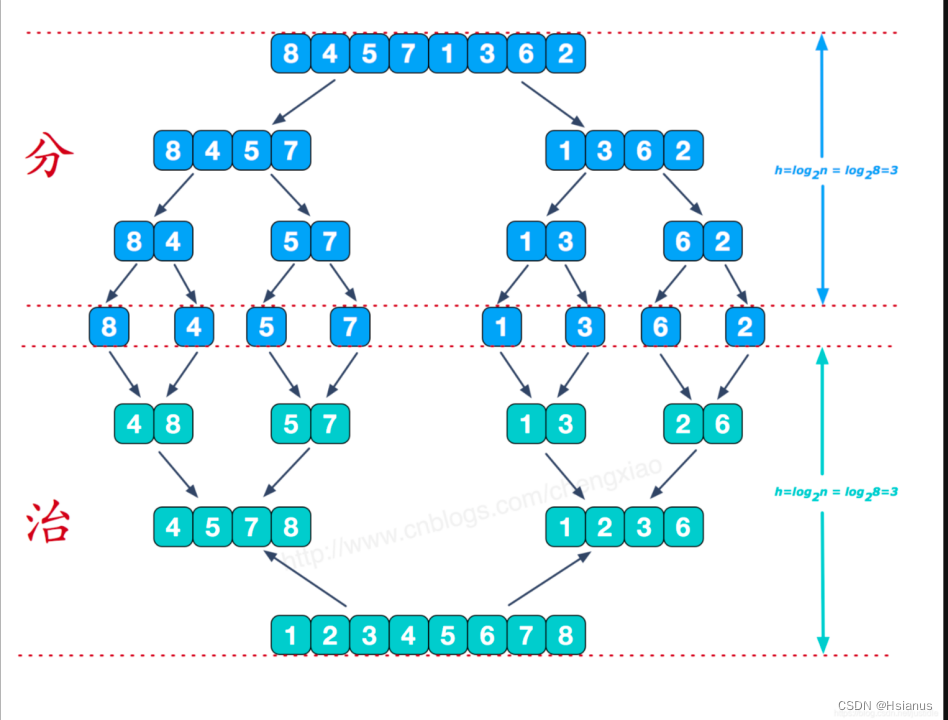
9.归并排序（稳定）

速度仅慢于快速排序，适用于分段有序的数列，为稳定排序算法。

9.1 基本思想（分治）：

1）只包含一个元素的子表是有序表

2）将有序的子表合并

3）得到最终表

4) 需要一个辅助的临时数组

9.2 代码实现：

void merge_sort_recursive(int r[],int reg[],int start,int end){
    if(start>=end){
        return;
    }
    int mid=(start+end)/2;
    merge_sort_recursive(r, reg, start, mid);
    merge_sort_recursive(r, reg, mid+1, end);
    //通过上述操作，已经获得了两个有序的子序列
    //合并
    int i=start,j=mid+1,k=start;
    while(i<=mid&&j<=end){
        if(r[i]<=r[j]){
            reg[k++]=r[i++];
        }
        else{
            reg[k++]=r[j++];
        }
    }
    while(i<=mid){
        reg[k++]=r[i++];
    }
    while(j<=end){
        reg[k++]=r[j++];
    }
    for(i=start;i<=end;i++){
        r[i]=reg[i];
    }
}
void merge_sort(int r[],int n){
    int reg[MAX_SIZE];//辅助数组
    merge_sort_recursive(r, reg, 0, n-1);
}

9.3 性能分析：

时间复杂度： $O(nlog_2n)$

空间复杂度：O(n)

10.排序方法比较

10.1 排序方法选择主要考虑：

1）待排序记录的数量

2）关键字的分布情况

3）对排序稳定性的要求

10.2 时间特性：

时间复杂度为 $O(nlog_2n)$ ：快速、归并

时间复杂度为 $O(n^2)$ ：插入、冒泡、选择

待排序记录基本有序时：插入和冒泡可以达到O(n)

选择、归并排序的时间特性不随关键字的分布而改变。

稳定排序：插入、冒泡、归并

不稳定：快速、选择、希尔

文章来源:https://blog.csdn.net/Hsianus/article/details/135191258
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！