关于时间与空间复杂度的学习
关于时间与空间复杂度的学习
算法时间复杂度定义
在进行算法分析时,语句总的执行次数 T(n) 是关于问题规模n的函数,进而分析T(n) 随n的变化情况并确定T(n) 的数量级。算法的时间复杂度,也就是算法的时间量度。记作:T(n)=O(f(n))。 它表示随问题n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐进时间复杂度,简称为时间复杂度。其中,f(n)是问题规模n的某个函数。
标准算法度量单位
渐近记号
1、Θ(big-theta)
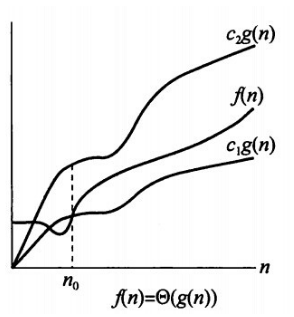
若存在正常量 c1、c2和n0 ,使得当 n ≥ n0 时,不等式0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) 恒成立,则称g(n)是f(n)的一个渐近紧确界,记作Θ。它包含渐近上界和渐近下界。
简单的理解为在 n ≥ n0 时,f(n)被夹在c1g(n)和c2g(n)之间,c1g(n)为f(n)的渐近下界,c2g(n)为f(n)的渐近上界,如下图所示。
2、O(big-oh)
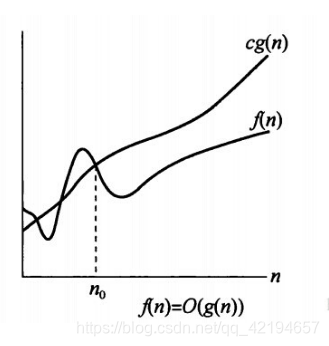
若存在正常量c和n0,使得当n ≥ n0 时,不等式 0 ≤ f(n) ≤ cg(n)恒成立,则称g(n)是f(n)的一个渐近上界,记作O。
简单的理解为在 n ≥ n0 时,cg(n)总是在f(n)之上。cg(n)为f(n)的渐近上界。如下图所示。
3、Ω(big-omege)
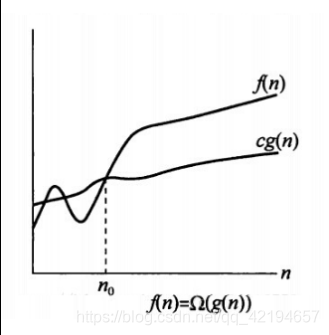
若存在正常量 c和n0,使得当 n ≥ n0 时,不等式 0 ≤ cg(n) ≤ f(n) 恒成立,则称g(n)是f(n)的一个渐近下界,记作Ω。
简单的理解为在 n ≥ n0 时,cg(n)总是在f(n)之下。cg(n)为f(n)的渐近下界。如下图所示。
我们使用O表示算法在最坏的情况下所代表的时间复杂度,Ω表示算法在最好的情况下所代表的时间复杂度,Θ表示算法在平均情况下所代表的时间复杂度。这个是算法书中比较标准的,现在网上大部分都直接用O来概括表示,这里理解就好。
这里看到网上的一片文章学习而来
原文链接:https://blog.csdn.net/qq_31116753/article/details/81602582
推导时间复杂度步骤与法则
步骤
-
找出算法中的基本语句;
算法中执行次数最多的那条语句就是基本语句,通常是最内层循环的循环体。 -
计算基本语句的执行次数的数量级;
计算基本语句执行次数的数量级,只保留最高阶项。这样能够简化算法分析,并且使注意力集中在最重要的一点上:增长率。 -
用常数1取代运行时间中的所有加法常数。
-
如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
O(log2n)、O(n)、O(nlog2n)、O(n2)和O(n3)称为多项式时间,而O(2n)和O(n!)称为指数时间。计算机科学家普遍认为前者是有效算法,把这类问题称为P(Polynomial,多项式)类问题,而把后者称为NP(Non-Deterministic Polynomial,非确定多项式)问题。
法则
-
对于一些简单的输入输出语句或赋值语句,近似认为需要O(1)时间
-
对于顺序结构,需要依次执行一系列语句所用的时间可采用大O下"求和法则" 求和法则:是指若算法的2个部分时间复杂度分别为 T1(n)=O(f(n))和 T2(n)=O(g(n)),则 T1(n)+T2(n)=O(max(f(n),g(n)))。特别地,若T1(m)=O(f(m)), T2(n)=O(g(n)),则 T1(m)+T2(n)=O(f(m)+g(n))
-
对于选择结构,如if语句,它的主要时间耗费是在执行then字句或else字句所用的时间,需注意的是检验条件也需要O(1)时间
-
对于循环结构,循环语句的运行时间主要体现在多次迭代中执行循环体以及检验循环条件的时间耗费,一般可用大O下"乘法法则"
乘法法则: 是指若算法的2个部分时间复杂度分别为 T1(n)=O(f(n))和 T2(n)=O(g(n)),则 T1*T2=O(f(n)*g(n)) -
对于复杂的算法,可以将它分成几个容易估算的部分,然后利用求和法则和乘法法则技术整个算法的时间复杂度
另外还有以下2个运算法则:(1) 若g(n)=O(f(n)),则O(f(n))+O(g(n))=O(f(n));(2)O(Cf(n)) = O(f(n)),其中C是一个正常数。
示例
1.常数阶
顺序额结构的复杂度。下面用高斯定理计算1,2,3…n个数的和。
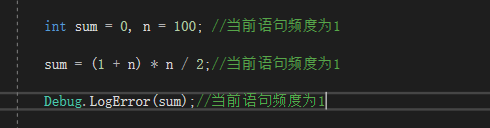
我们把这个元素当做一个函数来看待,该函数有三条语句记作f(n) = 3,根据上面的法则该函数不受n的影响且为常数项,所以时间复杂度记作O(1)。这种与问题的大小无关(n的多少),执行时间恒定的算法,我们称之为具有O(1)的时间复杂度,又叫常数阶。
2、线性阶
线性阶的循环结构会复杂很多。要确定某个算法的阶次,我们常常需要确定某个特定语句或某个语句集运行的次数。因此,我们要分析算法的复杂度,关键就是要分析循环结构的运行情况。

上图中1语句频度为1,
2语句频度为1,
3语句频度为1,
4语句频度为n,
5语句频度为n,
6语句频度为n
所以次函数记作f(n) = 1 + 1 + 1 + n + n + n = 3n + 3,根据法则所以该算法时间复杂度为O(n)。
3、对数阶
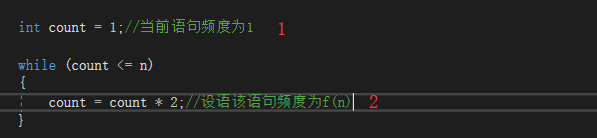
如上图所示,已知n>1
1语句频度为1,
2语句的频度为2^f(n) <= n
f(n) = log2^n
取最大值f(n) = log2^n
所以时间复杂度记作O(log2^n)。
4、平方阶

如上图所示
1语句频度为1,
2语句的频度为nn
f(n) = 1 + nn = n^2+1
所以时间复杂度记作O(n^2)。
5、立方阶

如上图所示
f(n) = 1 + nnn = n^3+1
所以时间复杂度记作O(n^3)。
扩展一个之前遇到的比较有意思的题


数学公式补充
公式一: 12/2+23/2+3*4/2+……+n(n+1)/2=n(n+1)(n+2)/6
公式二: 12+22+32+……+n2=n(n+1)(2n+1)/6
公式三: 13+23+33+……+n3=[n(n+1)/2]^2
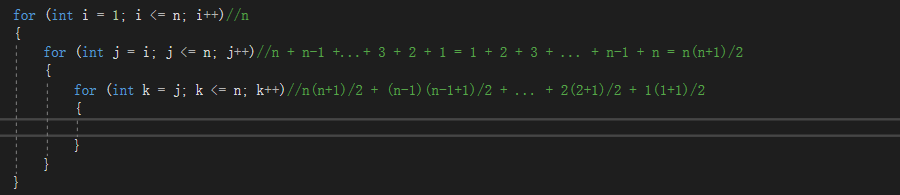
f(n) = n(n+1)(n+2)/6
= n(n^2 +3n +3)/6
= (n^3 + 3n^2 + 3n)/6
时间复杂度为O(n^3)
常见的时间复杂度比较
常用的时间复杂度所耗费的时间从小到大依次是:
O(1) < O(log2 ^ n) < O(n) < O(nlog2 ^ n) < O(n ^ 2) < O(n ^ 3) < O(2 ^ n) < O(n!) < O(n ^ n)
指数阶O(2^n)和阶乘阶O(n!)等除非是很小的n值,否则哪怕n 只是100,都是噩梦般的运行时间。所以这种不切实际的算法时间复杂度,一般我们都不去讨论。
最坏情况与平均情况
我们查找一个有n 个随机数字数组中的某个数字,最好的情况是第一个数字就是,那么算法的时间复杂度为O(1),但也有可能这个数字就在最后一个位置上待着,那么算法的时间复杂度就是O(n),这是最坏的一种情况了。
最坏情况运行时间是一种保证,那就是运行时间将不会再坏了。 在应用中,这是一种最重要的需求, 通常, 除非特别指定, 我们提到的运行时间都是最坏情况的运行时间。
而平均运行时间也就是从概率的角度看, 这个数字在每一个位置的可能性是相同的,所以平均的查找时间为n/2次后发现这个目标元素。平均运行时间是所有情况中最有意义的,因为它是期望的运行时间。也就是说,我们运行一段程序代码时,是希望看到平均运行时间的。可现实中,平均运行时间很难通过分析得到,一般都是通过运行一定数量的实验数据后估算出来的。一般在没有特殊说明的情况下,都是指最坏时间复杂度。
算法的空间复杂度
类似于时间复杂度的探讨,一个算法的空间复杂度S(n)定义为该算法所消耗的存储空间,它也是问题规模n的函数。渐近空间复杂度也常常简称为空间复杂度。空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。一个算法在计算机存储器上所占用的存储空间,包括存储算法本身所占用的存储空间,算法的输入输出所占用的存储空间和算法在运行过程中临时占用的存储空间这三个方面。算法的输入输出数据所占用的存储空间是由要解决的问题决定的,是通过参数表由调用函数传递而来的,它不随本算法的不同而改变。存储算法本身所占用的存储空间与算法书写的长短成正比,要压缩这方面的存储空间,就必须编写出较短的算法。算法在运行过程中临时占用的存储空间随算法的不同而异,有的算法只需要占用少量的临时工作单元,而且不随问题规模的大小而改变,我们称这种算法是“就地进行的”,是节省存储的算法,如上面介绍的都是。有的算法需要占用的临时工作单元数与解决问题的规模n有关,它随着n的增大而增大,当n较大时,将占用较多的存储单元。
当一个算法的空间复杂度为一个常量,即不随被处理数据量n的大小而改变时,可表示为O(1);当一个算法的空间复杂度与以2为底的n的对数成正比时,可表示为0(log2^n);当一个算法的空间复杂度与n成线性比例关系时,可表示为0(n).若形参为数组,则只需要为它分配一个存储由实参传送来的一个地址指针的空间,即一个机器字长空间;若形参为引用方式,则也只需要为其分配存储一个地址的空间,用它来存储对应实参变量的地址,以便由系统自动引用实参变量。
算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算公式记作:S(n)= O(f(n)),其中,n为问题的规模,f(n)为语句关于n所占存储空间的函数。
一般情况下,一个程序在机器上执行时,除了需要存储程序本身的指令、常数、变量和输入数据外,还需要存储对数据操作的存储单元。若输入数据所占空间只取决于问题本身,和算法无关,这样只需要分析该算法在实现时所需的辅助单元即可。若算法执行时所需的辅助空间相对于输入数据量而言是个常数,则称此算法为原地工作,空间复杂度为O(1)。关于O(1)的问题, O(1)是说数据规模和临时变量数目无关,并不是说仅仅定义一个临时变量。举例:无论数据规模多大,我都定义100个变量,这就叫做数据规模和临时变量数目无关。就是说空间复杂度是O(1)。
对于一个算法,其时间复杂度和空间复杂度往往是相互影响的。当追求一个较好的时间复杂度时,可能会使空间复杂度的性能变差,即可能导致占用较多的存储空间;反之,求一个较好的空间复杂度时,可能会使时间复杂度的性能变差,即可能导致占用较长的运行时间。另外,算法的所有性能之间都存在着或多或少的相互影响。因此,当设计一个算法(特别是大型算法)时,要综合考虑算法的各项性能,算法的使用频率,算法处理的数据量的大小,算法描述语言的特性,算法运行的机器系统环境等各方面因素,才能够设计出比较好的算法。
常用的算法的时间复杂度和空间复杂度
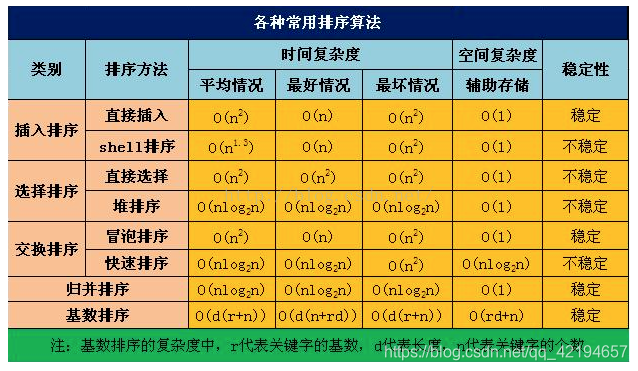
一些计算的规则
1、加法规则
T(n,m) = T1(n) + T2(m) = O(max{f(n), g(m)})
2、乘法规则
T(n,m) = T1(n) * T2(m) = O(max{f(n)*g(m)})
3、复杂度与时间效率的关系
c(常数) < logn < n < n*logn < n^2 < n^3 < 2^n < 3^n < n!
l------------------------------l--------------------------l--------------l
较好 一般 较差
原文连接:https://blog.csdn.net/daijin888888/article/details/66970902#commentBox
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- http跟https有什么区别?
- Vue 点击按钮复制内容到系统剪贴板
- stm32用cubemx开发HAL库串口协议控制PWM灯亮度带proteus仿真(一)硬件配置
- HarmonyOS-@Watch装饰器:状态变量更改通知
- 基于SpringBoot+Vue的田径运动会成绩管理系统设计实现(源码+lw+部署文档+讲解等)
- 074:vue+mapbox 加载here地图(影像瓦片图 v2版)
- HBuilder 新建的项目实现全局格式化
- k8s之pod基础
- Web基础与http协议
- LCR 143. 子结构判断