数据结构与算法：归并排序

---

归并思想

在讲解归并排序前，我们先看到一个问题：

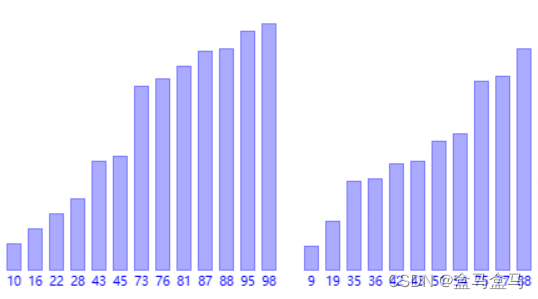
对于这样两个有序的数组，如何将它们合并为一个有序的数组？

在此我们处理这个问题的思路就是：开辟一个新的数组，然后分别安置一个指针在左右数组，利用指针遍历数组，每次对比将比较小的那个元素插入到数组的尾部。
像这样：

那么我们要如何利用这个思想，让一个无序的数组有序？

比如这个数组：

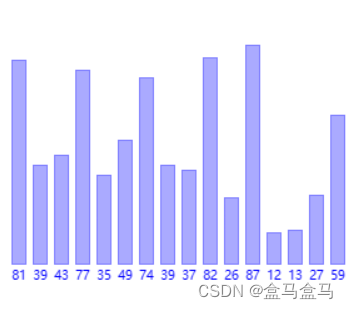
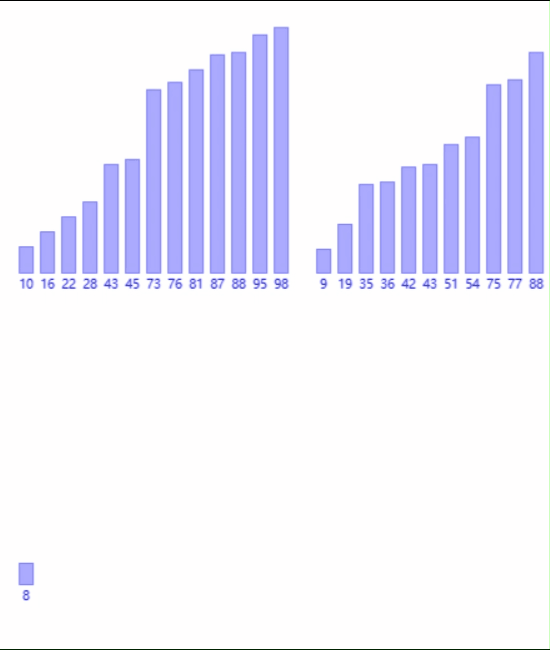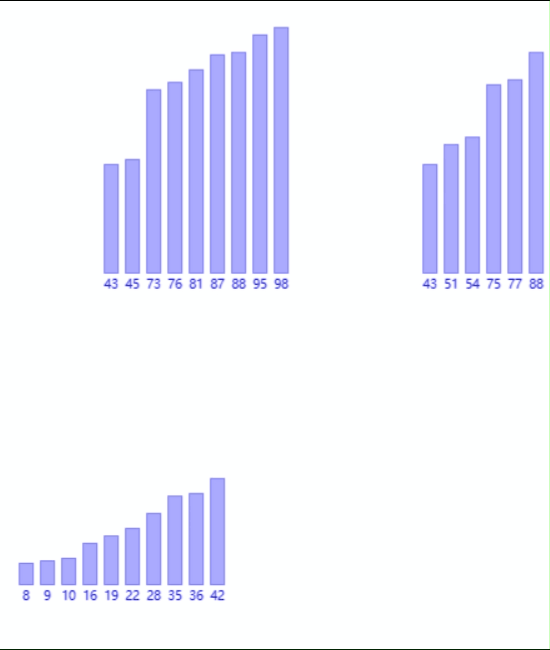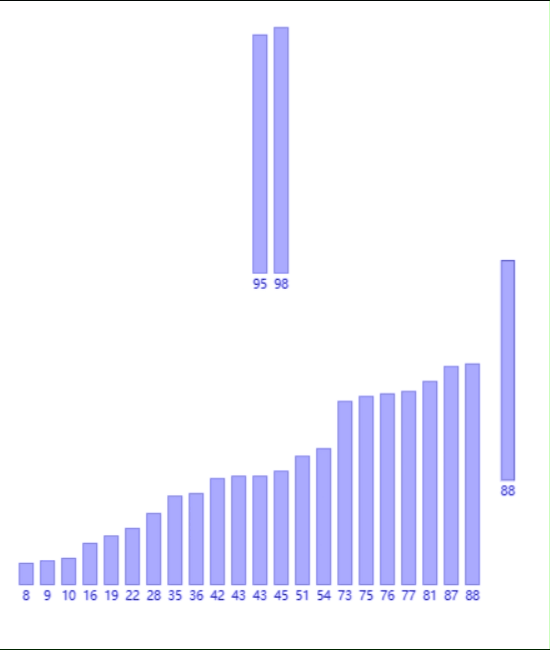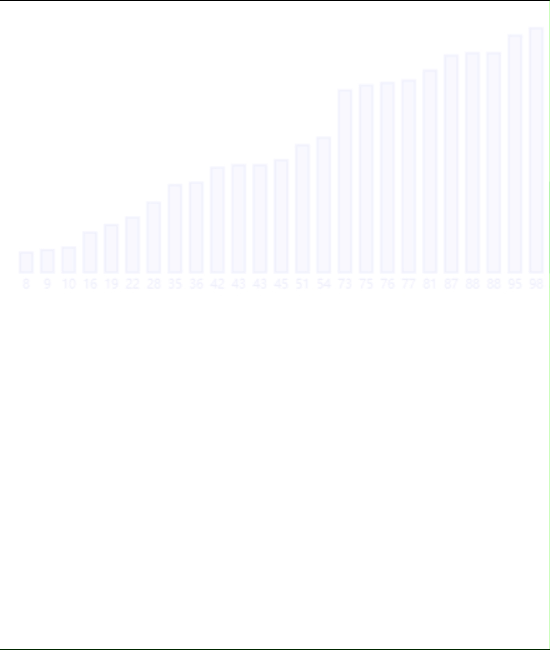
我们可以这样划分数组：

将其不断往小份划分，划分到最后一段：

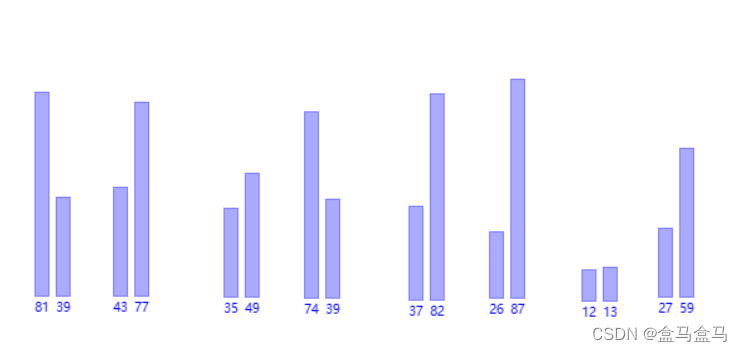
对于每一个区域，我们可以认为：左边的一个元素是一个有序数组，右边的一个元素是一个有序数组。然后在对其进行一次归并。

就像这样：

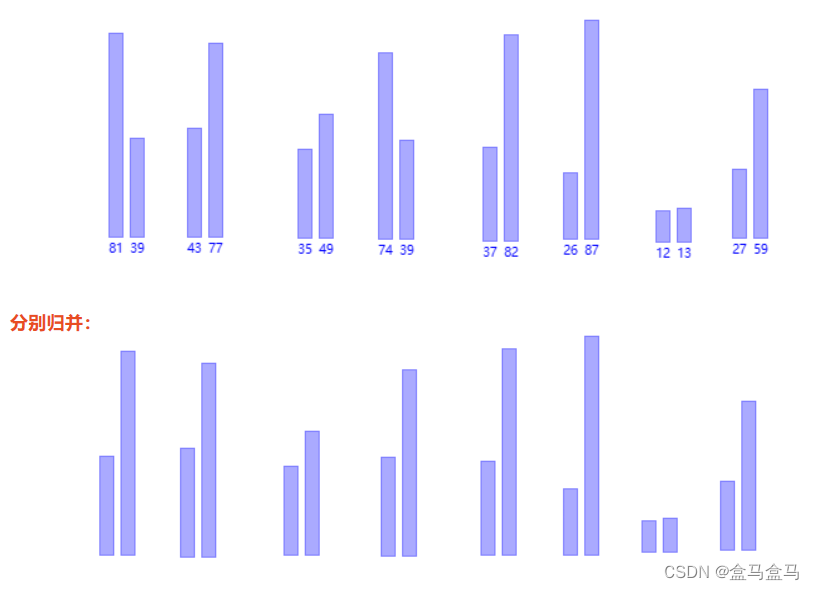
这样我们又得到了8组有序的数组，我们继续归并：

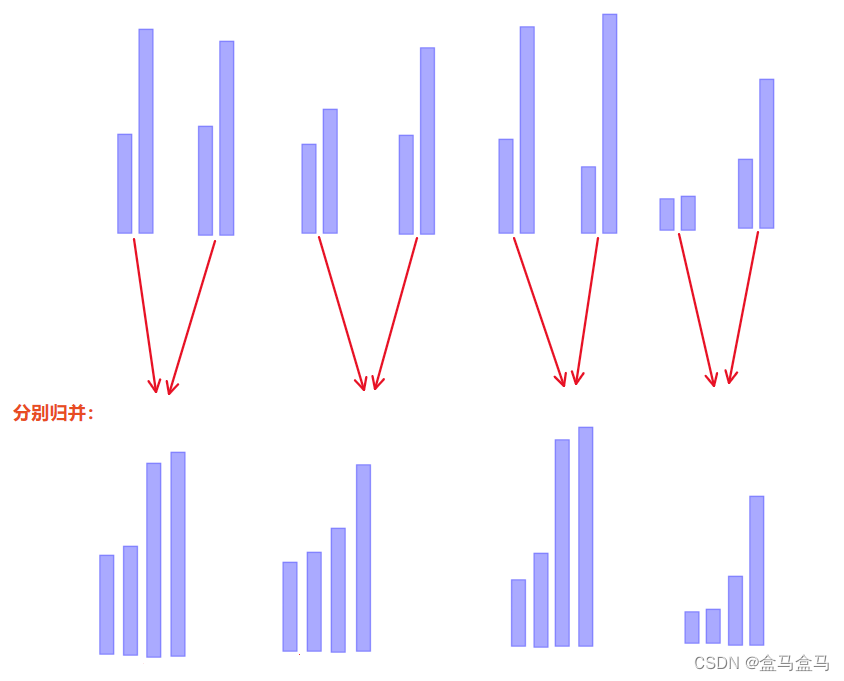
以此类推：

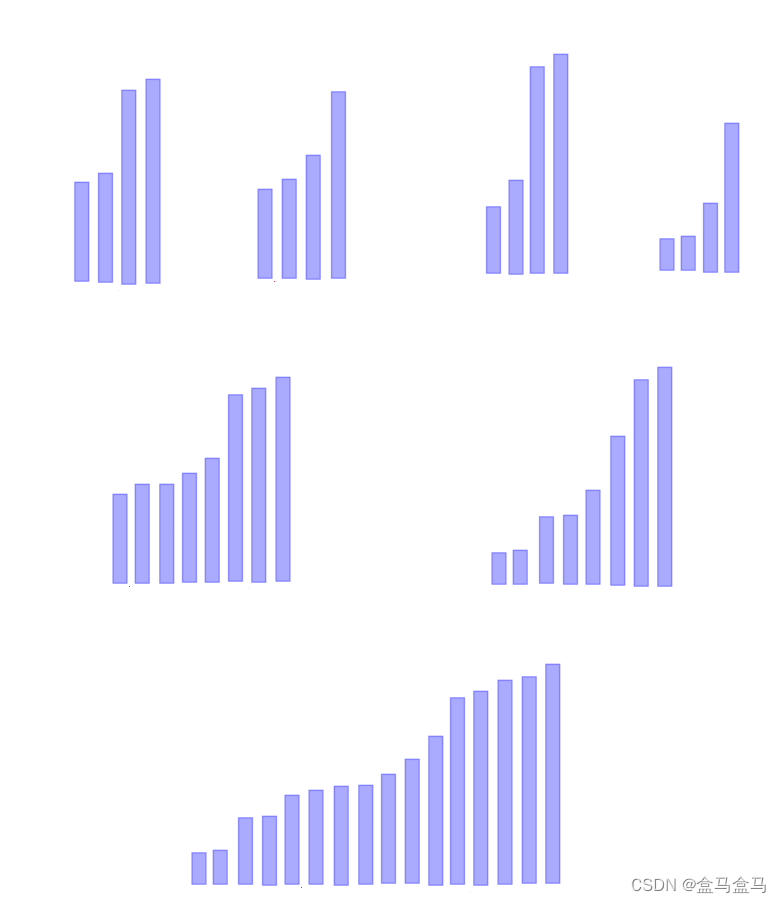
归并排序就是这样一个不断划分子区间，然后进行合并的过程。

---

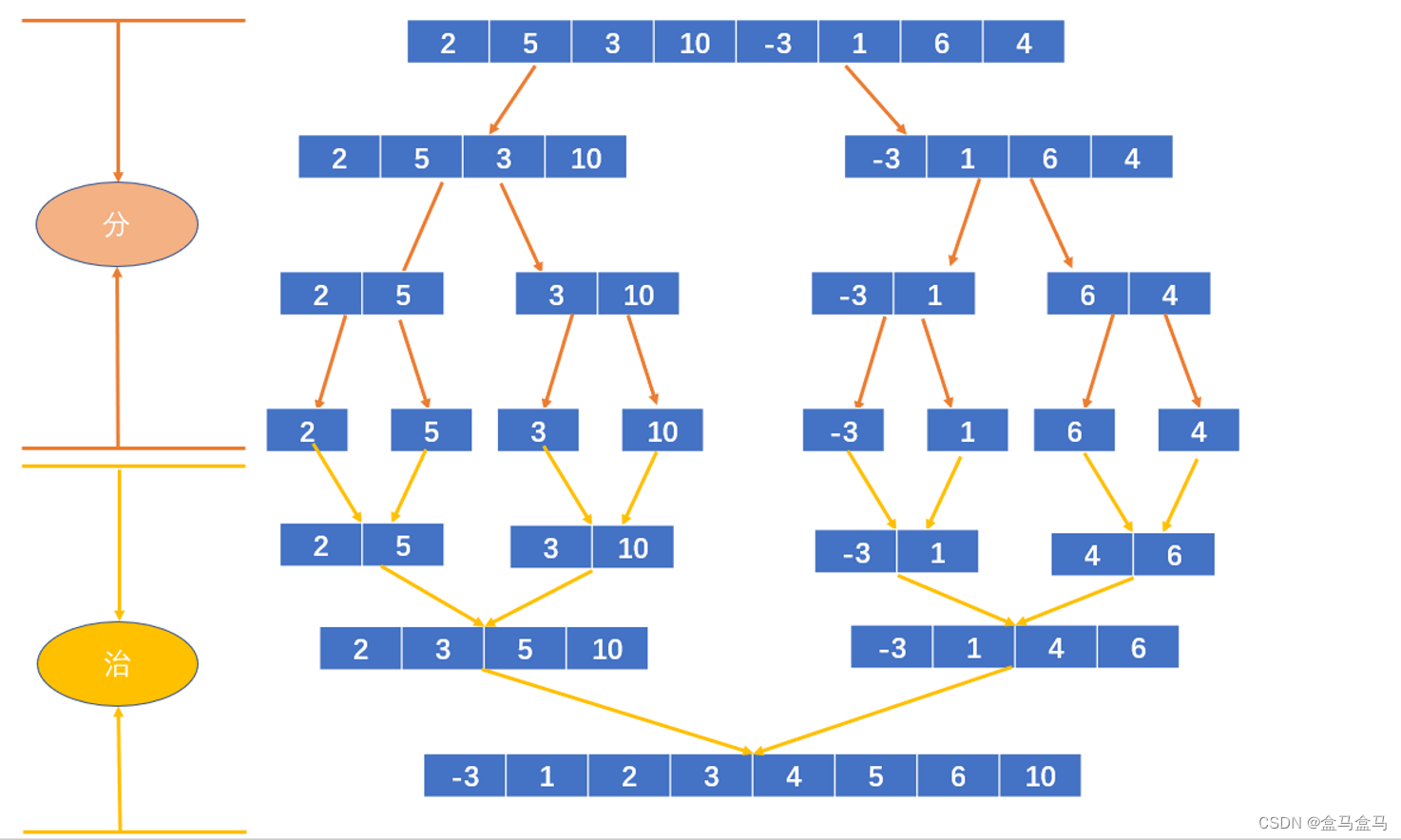
递归法

看到不断划分出子区间，毫无疑问这将会是一个递归的过程，而我们将子区间划分到底，再进行处理数据，所以这是同样是一个后序遍历的过程。

在进行合并数组的时候，我们会需要开辟一个新的数组来存放临时的数据。
如果每次合并数组时都额外开辟一段空间，就有点浪费时间了，空间是可以重复利用的，所以我们一开始就要开辟一个和原数组等大的空间。后序进行合并操作都在这个拷贝数组中，当合并完成后，再把数组复制回原数组即可。

那么我们的归并排序一开始要这样写，

void _MergeSort(int* a, int begin, int end, int* tmp)
{
	//归并主体
}

void MergeSort(int* a, int n)
{
	int*
	 tmp = (int*)malloc(sizeof(int) * n);//开辟空间
	if (tmp == NULL)
	{
		perror("malloc fali!");
		return;
	}

	_MergeSort(a, 0, n - 1, tmp);//归并主体

	free(tmp);
}

_MergeSort函数是归并排序的主体函数，它接受一个待排序的数组a、数组的起始位置begin、数组的结束位置end以及一个临时数组tmp。函数中实现了归并排序的核心部分，即将数组a中的元素从位置begin到位置end进行排序。

MergeSort函数是对_MergeSort函数的封装，它接受一个待排序的数组a和数组的长度n。函数中首先动态分配了一个大小为n的临时数组tmp，用于存放归并时的临时数据，然后调用_MergeSort函数对数组a进行归并排序。排序完成后，释放临时数组tmp的空间。

接下来我们完成归并主体的代码：

void _MergeSort(int* a, int begin, int end, int* tmp)
{
	if (begin >= end)
		return;

	int mid = (begin + end) / 2;
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid + 1, end, tmp);

	//归并
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;

	int i = begin;//使拷贝的数组与原数组的位置对应
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}

	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}

	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}

下面是代码的详细步骤解释：

1. 首先定义了一个名为_MergeSort的函数，它接受四个参数：需要排序的数组a、排序区间的起始位置begin和结束位置end，以及一个临时数组tmp。

---

2. 如果begin大于等于end，说明只有一个元素或者没有元素，直接返回。

---

3. 否则，计算出中间位置mid，将数组分为左右两个子数组。

---

4. 对左右两个子数组分别调用_MergeSort函数进行递归排序，直到只剩下一个元素。

---

5. 接下来进行归并操作。定义四个变量begin1、end1、begin2、end2，分别表示左右子数组的起始和结束位置。

---

6. 定义一个变量i，用于标记临时数组tmp的位置。

---

7. 开始合并过程，比较左右子数组的元素大小，将较小的元素放入临时数组tmp中，并递增i和对应的子数组起始位置。

---

8. 如果有一边的子数组已经合并完毕（起始位置大于结束位置），则将另一边的子数组中剩余的元素依次放入临时数组tmp中。

---

9. 最后，使用memcpy函数将临时数组tmp中的元素拷贝回原数组a的对应位置。

通过不断递归划分数组为更小的子数组，并借助临时数组tmp进行归并操作，最终完成整个归并排序的过程。

总过程如下：

---

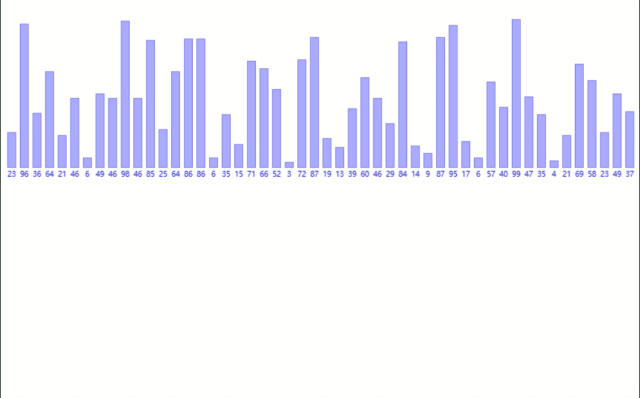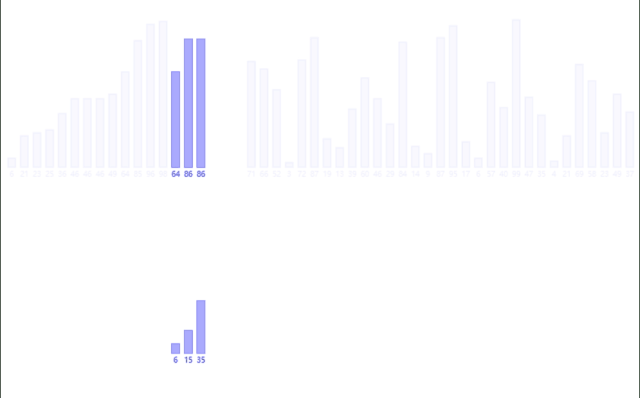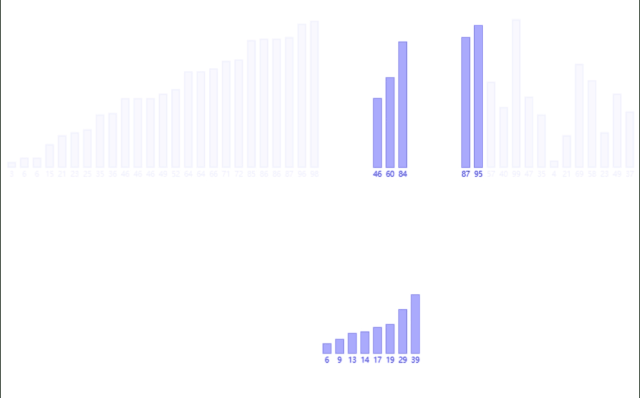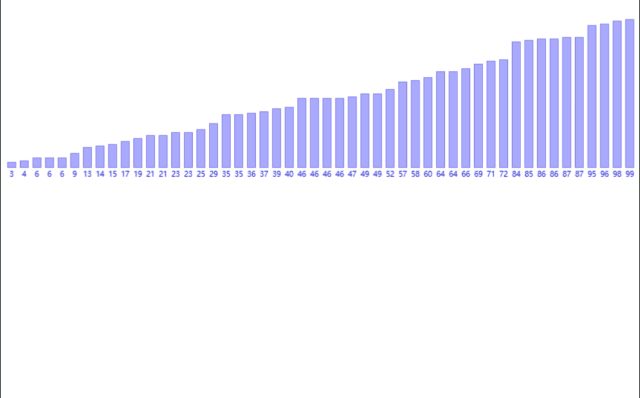
非递归

其实归并排序也可以使用非递归的方法实现：

我们再次看到这个归并排序的递归图：

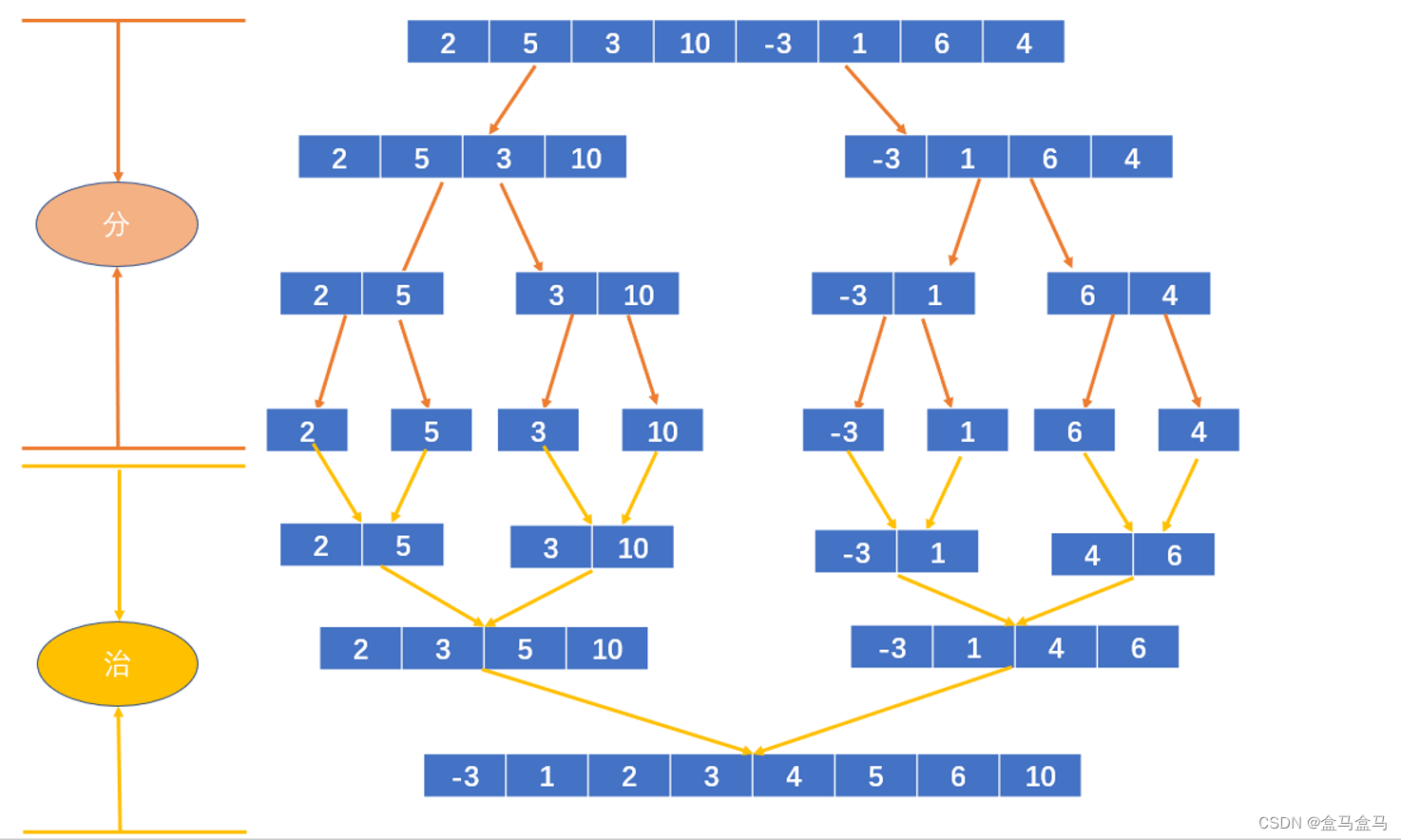
可以发现，由于是后序遍历，其实前面在利用递归对数组划分的过程，我们并没有对数组进行任何修改，也就是说我们可以直接把数组划分到每一组只有1个元素，来模拟前半部分的递归。
像这样：

int gap = 1;
for (int i = 0; i < n; i += 2 * gap)
{
	//归并数组
}

在这段代码中，变量 gap 初始化为 1，表示每次归并操作对应的子数组的长度。初始时，我们假定待合并的子数组的长度为 1，来模仿前半部分递归划分出来的子数组。
i += 2 * gap意味着每次跳过两个子数组，一个gap是一个子数组的长度，2 * gap就是两个子数组的长度。这模仿的是每次合并数组时，被合并的数组区间划分。

那么我们完成了前半部分递归，直接把数组划分为了只有一个元素的小区间，那要如何模仿后半部分？
递归后半部分的工作是，将小区间归并后，形成了一个大区间，接着再把大区间归并，直到这个区间等于原数组长度。
我们想用非递归的思路来模仿后半部分，也就是要实现每次归并区间的增大。
那么每次归并的区间增大多少？
因为每次合并时，是合并了左右两个长度相同的数组，所以归并出的新数组长度应该是2*gap，所以我们每一趟归并，都要把gap翻倍，来模仿区间被合并后增大的效果：

void MergeSortNonR(int* a, int n)
{
	int gap = 1;

	while (gap < n)//当gap超过n，说明数组合并完毕了
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			//归并主体
		}
		gap *= 2;//归并完后，下一趟归并的区间翻倍
	}
}

那么每次划分出了归并的区间，又要如何划分其内部的两个子数组？
比如这样：

void MergeSortNonR(int* a, int n)
{
	int gap = 1;

	while (gap < n)//当gap超过n，说明数组合并完毕了
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			//对[begin1, end1][begin2, end2]归并
			
			//归并主体
		}
		gap *= 2;//归并完后，下一趟归并的区间翻倍
	}
}

根据这串代码，我们在一个2 * gap范围内，每个gap都是一个子数组，紧接着我们就可以对两个子数组[begin1, end1]和[begin2, end2]归并。

但是这样会产生一个问题，那就是数组的尾部越界了。
我们不能保证每次gap的值都可以被数组整除，所以最后一段gap是有可能会越界的，这要如何控制？

我们一一分析：

对于begin1：

由于begin1 = i而i < n，所以begin1一定不可能越界。

对于end1 和 begin2：

我们每次归并时，会得到两个已经有序的子区间[begin1, end1]和[begin2, end2]，如果end1 和 begin2越界，可以理解为[begin2, end2]整个区间都越界了，而[begin1, end1]尚未越界。但是[begin1, end1]是一个已经有序的子区间，所以此时可以不用归并了，直接break，跳过本趟归并。

对于end2：

当end2越界，相当于是子区间[begin2, end2]有一部分在数组中，有一部分越界。而存在于数组中的那一部分就是[begin2, n - 1]，所以此时我们需要将end2的值改为n-1。
让区间[begin1, end1]和[begin2, n - 1]进行归并。

综上我们的非递归大体骨架如下：

void MergeSortNonR(int* a, int n)
{
	int gap = 1;//第一趟归并，每个子区间长度为1

	while (gap < n)//当gap超过n，说明数组合并完毕了
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			//防止越界处理
			if (end1 > n || begin2 > n)
			{
				break;
			}

			if (end2 > n)
			{
				end2 = n - 1;
			}
			
			//归并主体
		}
		gap *= 2;//归并完后，下一趟归并的区间翻倍
	}
}

而归并主体部分已经讲解过，就是利用两个指针，每次取出最小的元素插入到新的数组中，再将新数组拷贝回去。

总代码如下：

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fali!");
		return;
	}

	int gap = 1;

	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			if (end1 > n || begin2 > n)
			{
				break;
			}

			if (end2 > n)
			{
				end2 = n - 1;
			}

			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
		}

		gap *= 2;
	}

	free(tmp);
}

---