凤凰架构之事务处理

本地事务

本地事务是最基础的一种事务解决方案，只适用于单个服务使用单个数据源的场景。从应用角度看，它是直接依赖于数据源本身提供的事务能力来工作的，在程序代码层面，最多只能对事务接口做一层标准化的包装（如 JDBC 接口），并不能深入参与到事务的运作过程当中，事务的开启、终止、提交、回滚、嵌套、设置隔离级别，乃至与应用代码贴近的事务传播方式，全部都要依赖底层数据源的支持才能工作，这一点与后续介绍的 XA、TCC、SAGA 等主要靠应用程序代码来实现的事务有着十分明显的区别。

本地事务：单服务单数据源
事务特性：ACID
原子性和持久性：commit Logging
write ahead Logging
隔离性：加锁
写锁：
读锁：
范围锁：锁住的是一段范围；被锁住的范围内，数据不能被修改，不能在这个范围内进行新增和删除操作，区别于一组 排他锁

事务隔离级别，从高到底分别为：
串行化：读锁，写锁和范围锁（并发度低，性能较差）
可重复读：整个事务过程中加读锁和写锁，mysql只读事务不会出现幻读，读写事务幻读问题仍然存在
读已提交：整个事务过程加写锁，读锁在查询结束后就马上释放，容易出现不可重复读的问题
读未提交：整个事务过程加写锁，但完全不加读锁，容易出现脏读问题，即两次查询读取结果不一样

幻读：它是指在事务执行过程中，两个完全相同的范围查询得到了不同的结果集。

SELECT count(1) FROM books WHERE price < 100					/* 时间顺序：1，事务： T1 */
INSERT INTO books(name,price) VALUES ('深入理解Java虚拟机',90)	/* 时间顺序：2，事务： T2 */
SELECT count(1) FROM books WHERE price < 100					/* 时间顺序：3，事务： T1 */

不可重复读：它是指在事务执行过程中，对同一行数据的两次查询得到了不同的结果。

SELECT * FROM books WHERE id = 1;   						/* 时间顺序：1，事务： T1 */
UPDATE books SET price = 110 WHERE id = 1; COMMIT;			/* 时间顺序：2，事务： T2 */
SELECT * FROM books WHERE id = 1; COMMIT;   				/* 时间顺序：3，事务： T1 */

脏读：它是指在事务执行过程中，一个事务读取到了另一个事务未提交的数据。

SELECT * FROM books WHERE id = 1;   						/* 时间顺序：1，事务： T1 */
/* 注意没有COMMIT */
UPDATE books SET price = 90 WHERE id = 1;					/* 时间顺序：2，事务： T2 */
/* 这条SELECT模拟购书的操作的逻辑 */
SELECT * FROM books WHERE id = 1;			  				/* 时间顺序：3，事务： T1 */
ROLLBACK;			  										/* 时间顺序：4，事务： T2 */

除了都以锁来实现外，以上四种隔离级别还有另一个共同特点，就是幻读、不可重复读、脏读等问题都是由于一个事务在读数据过程中，受另外一个写数据的事务影响而破坏了隔离性，针对这种“一个事务读+另一个事务写”的隔离问题出现了多版本并发控制的无锁优化方案。
mvcc (multi-version concurrency controller):MVCC 的基本思路是对数据库的任何修改都不会直接覆盖之前的数据，而是产生一个新版副本与老版本共存，以此达到读取时可以完全不加锁的目的.
可以理解为数据库中每一行记录存在两个看不见的字段CREATE_VERSION 和 DELETE_VERSION，这两字字段记录的值是事务ID,事务id是递增的。

mvcc主要针对的是可重复读和读已提交的隔离级别出现的读和写出现的问题，一个事务读一个事务写

乐观锁：事务写+写场景
悲观锁：以上锁均属于悲观锁

乐观锁：在操作数据的时候非常乐观，乐观锁默认是不会上锁的，只有在执行更新的时候才会去判断在此期间别人是否修改了数据，如果别人修改了数据则放弃操作，否则执行操作。在乐观锁中，数据被读的时候不会加锁，但在更新数据的时候会判断在此期间有没有其他用户修改过这个数据，若有其他用户修改过这个数据，则该用户提交更新操作会被阻塞，转而执行其他操作。
悲观锁：在操作数据的时候比较悲观，悲观地认为别人一定会同时修改数据，因此悲观锁在操作数据时是直接把数据上锁，直到操作完成之后才会释放锁。在悲观锁中，数据被读的时候会被锁定，其他用户无法进行读取或者写入，只能等待锁被释放。

全局事务

全局事务：单服务多数据源
XA 是 （extended Architecture 的缩写）的处理事务架构，其核心内容是定义了全局的事务管理器（Transaction Manager，用于协调全局事务）和局部的资源管理器（Resource Manager，用于驱动本地事务）之间的通信接口。XA 接口是双向的，能在一个事务管理器和多个资源管理器（Resource Manager）之间形成通信桥梁，通过协调多个数据源的一致动作，实现全局事务的统一提交或者统一回滚，是一套语言无关的通用规范。
二段式提交协议：
准备阶段：（又叫投票阶段）协调者询问事务的所有参与者是否准备好提交，参与者如果已经准备好提交则回复 Prepared，否则回复 Non-Prepared
提交阶段：（又叫执行阶段）

缺点：
1.单点问题：如果协调者宕机，一直没有恢复，没有正常发送 Commit 或者 Rollback 的指令，那所有参与者都必须一直等待
2.性能问题：
3.一致性风险：数据不一致

三段式提交协议：
CanCommit:(询问阶段)，协调者让每个参与的数据库根据自身状态，评估该事务是否有可能顺利完成
PreCommit:准备阶段
DoCommit:提交阶段

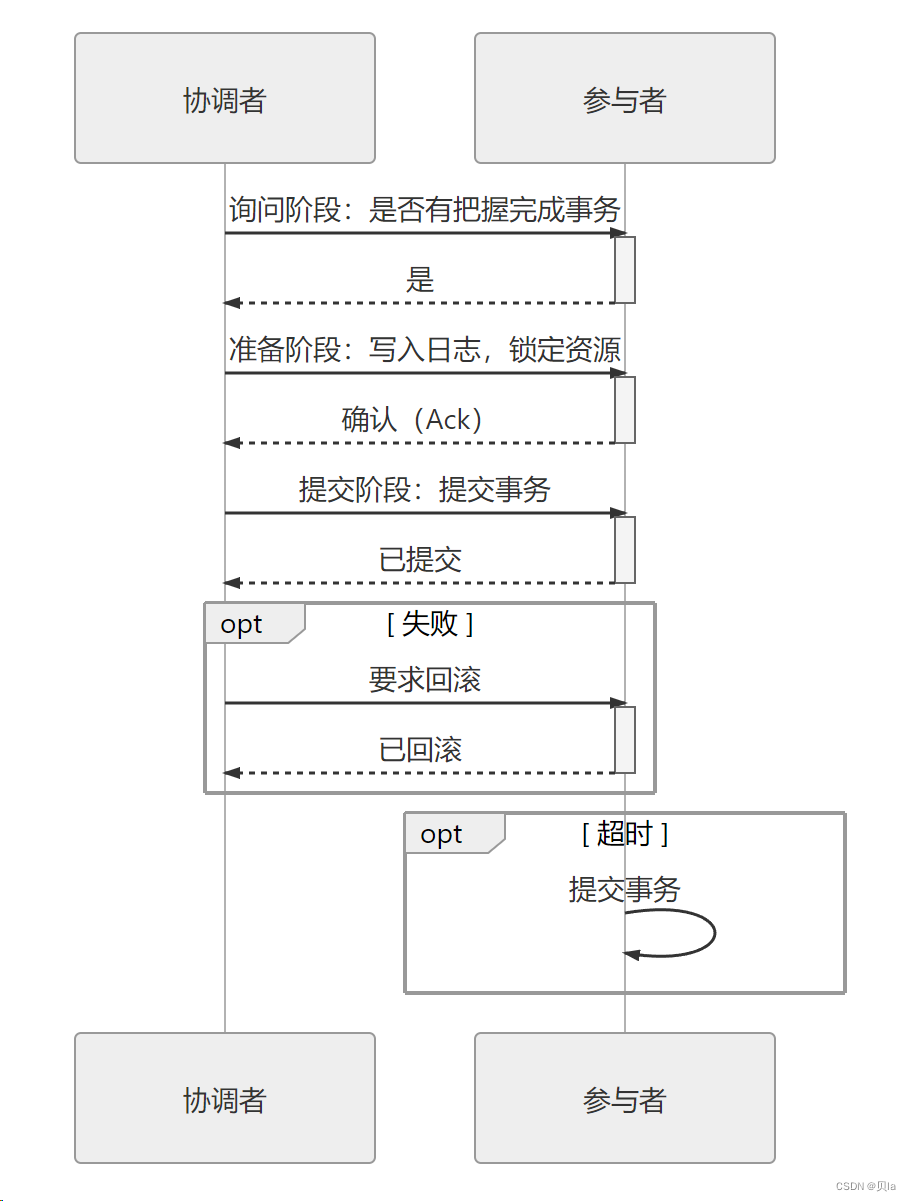
三段式提交对单点问题和回滚时的性能问题有所改善，但是它对一致性风险问题并未有任何改进，在这方面它面临的风险甚至反而是略有增加了的。譬如，进入 PreCommit 阶段之后，协调者发出的指令不是 Ack 而是 Abort，而此时因网络问题，有部分参与者直至超时都未能收到协调者的 Abort 指令的话，这些参与者将会错误地提交事务，这就产生了不同参与者之间数据不一致的问题。

共享事务

共享事务：多个服务共用一个数据源

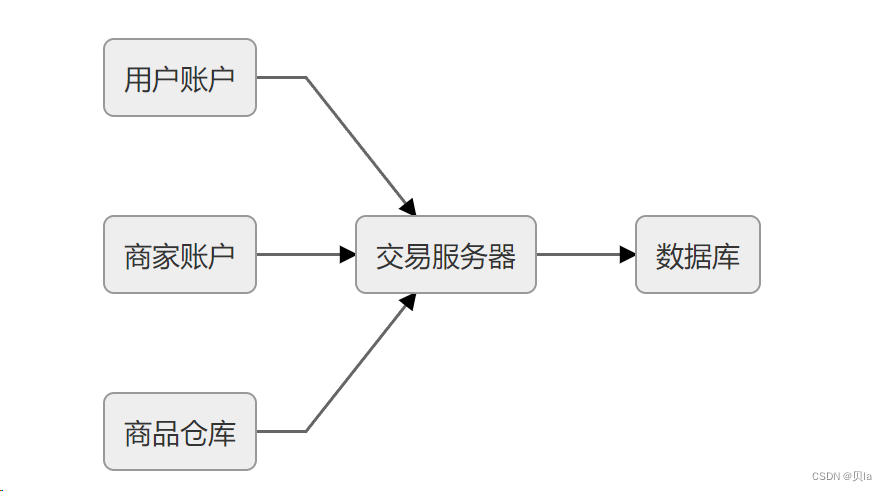
一种理论可行的方案是直接让各个服务共享数据库连接

分布式事务

分布式事务（Distributed Transaction）特指多个服务同时访问多个数据源的事务处理机制
“在分布式服务环境下的事务处理机制”
CAP 定理（Consistency、Availability、Partition Tolerance Theorem），也称为 Brewer 定理；起源于在 2000 年 7 月，是加州大学伯克利分校的 Eric Brewer 教授于“ACM 分布式计算原理研讨会（PODC）”上提出的一个猜想。
一致性（Consistency）：代表数据在任何时刻、任何分布式节点中所看到的都是符合预期的。
可用性（Availability）：代表系统不间断地提供服务的能力，可用性衡量系统可以正常使用的时间与总时间之比，其表征为：A=MTBF/（MTBF+MTTR），即可用性是由可靠性和可维护性计算得出的比例值，譬如 99.9999%可用，即代表平均年故障修复时间为 32 秒。
分区容忍性：代表分布式环境中部分节点因网络原因而彼此失联后，即与其他节点形成“网络分区”时，系统仍能正确地提供服务的能力。
择放弃一致性的 AP 系统目前是设计分布式系统的主流选择，AP,CP
分布式系统设计最终一致性，很难达到强一致性。
最终一致性 (opens new window)（Eventual Consistency），它是指：如果数据在一段时间之内没有被另外的操作所更改，那它最终将会达到与强一致性过程相同的结果，有时候面向最终一致性的算法也被称为“乐观复制算法”。

可靠消息队列

可靠事件队列还有一种更普通的形式，被称为“最大努力一次提交”（Best-Effort 1PC），指的就是将最有可能出错的业务以本地事务的方式完成后，采用不断重试的方式（不限于消息系统）来促使同一个分布式事务中的其他关联业务全部完成。

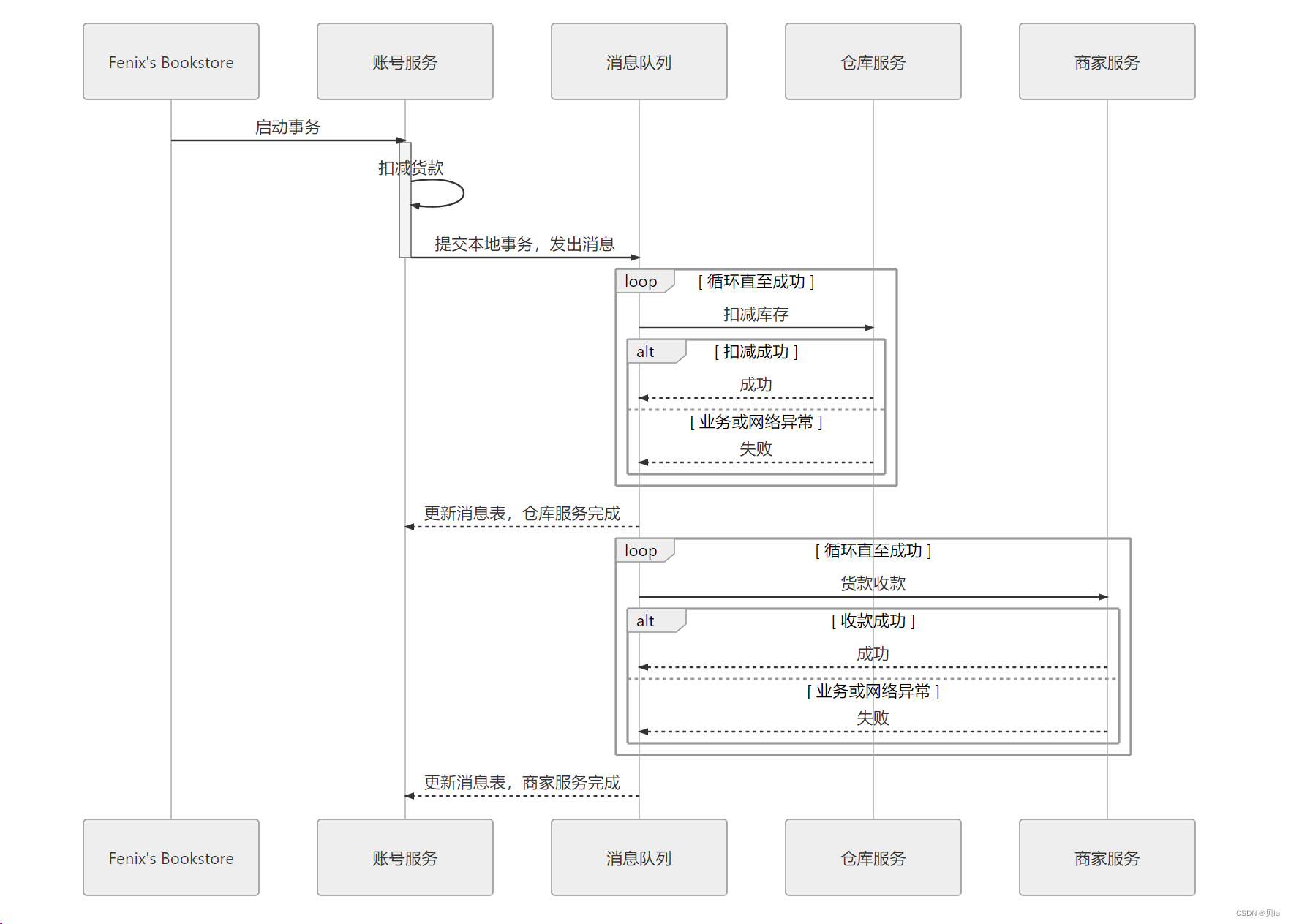
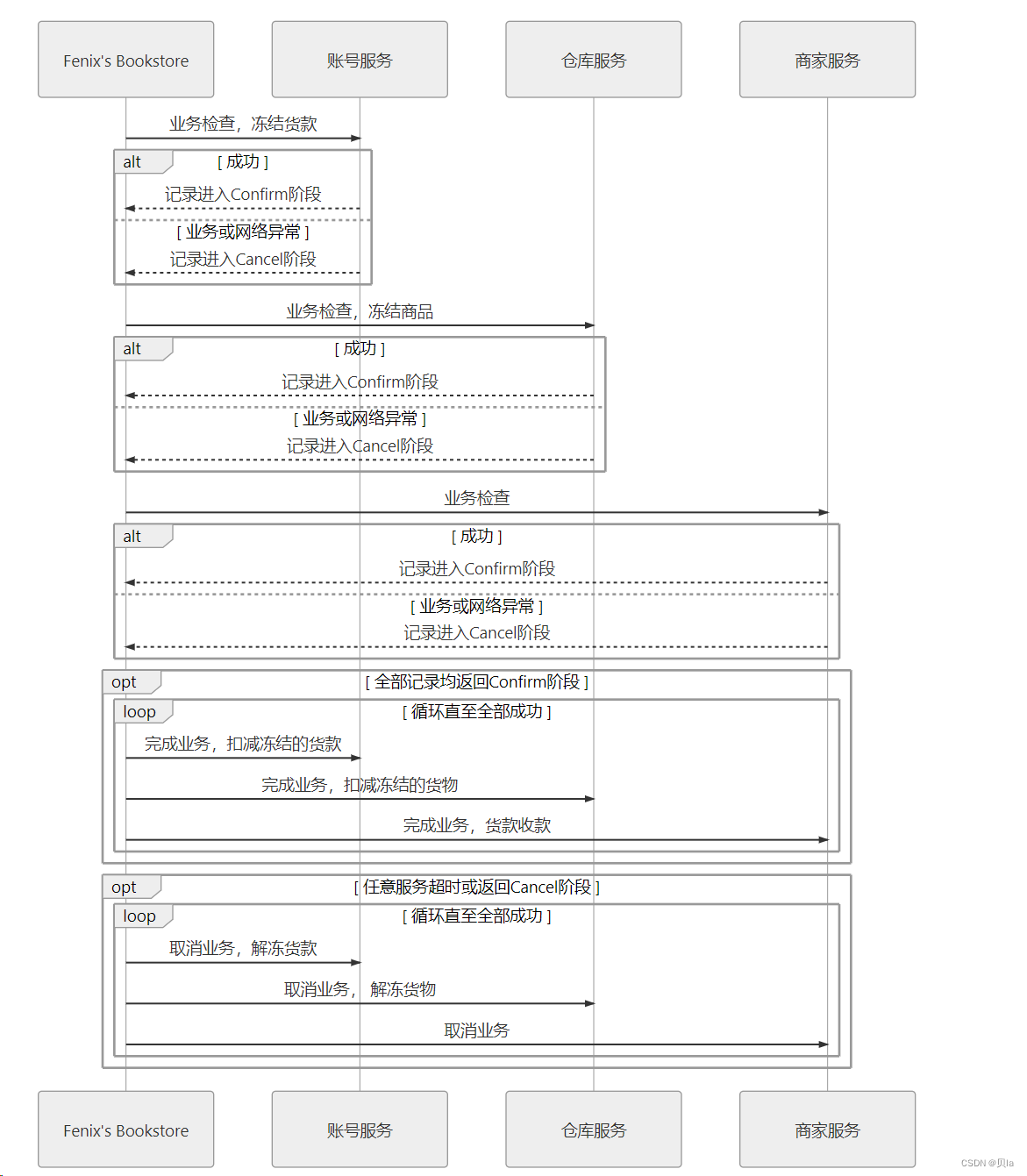
TCC事务

TCC 是另一种常见的分布式事务机制，它是“Try-Confirm-Cancel”三个单词的缩写
Try：尝试执行阶段，完成所有业务可执行性的检查（保障一致性），并且预留好全部需用到的业务资源（保障隔离性）。
Confirm：确认执行阶段，不进行任何业务检查，直接使用 Try 阶段准备的资源来完成业务处理。Confirm 阶段可能会重复执行，因此本阶段所执行的操作需要具备幂等性。
Cancel：取消执行阶段，释放 Try 阶段预留的业务资源。Cancel 阶段可能会重复执行，也需要满足幂等性

SAGA事务

SAGA 由两部分操作组成。

大事务拆分若干个小事务，将整个分布式事务 T 分解为 n 个子事务，命名为 T1，T2，…，Ti，…，Tn。每个子事务都应该是或者能被视为是原子行为。如果分布式事务能够正常提交，其对数据的影响（最终一致性）应与连续按顺序成功提交 Ti等价。
为每一个子事务设计对应的补偿动作，命名为 C1，C2，…，Ci，…，Cn。Ti与 Ci必须满足以下条件：
Ti与 Ci都具备幂等性。
Ti与 Ci满足交换律（Commutative），即先执行 Ti还是先执行 Ci，其效果都是一样的。
Ci必须能成功提交，即不考虑 Ci本身提交失败被回滚的情形，如出现就必须持续重试直至成功，或者要人工介入。
如果 T1到 Tn均成功提交，那事务顺利完成，否则，要采取以下两种恢复策略之一：

正向恢复（Forward Recovery）：如果 Ti事务提交失败，则一直对 Ti进行重试，直至成功为止（最大努力交付）。这种恢复方式不需要补偿，适用于事务最终都要成功的场景，譬如在别人的银行账号中扣了款，就一定要给别人发货。正向恢复的执行模式为：T1，T2，…，Ti（失败），Ti（重试）…，Ti+1，…，Tn。
反向恢复（Backward Recovery）：如果 Ti事务提交失败，则一直执行 Ci对 Ti进行补偿，直至成功为止（最大努力交付）。这里要求 Ci必须（在持续重试后）执行成功。反向恢复的执行模式为：T1，T2，…，Ti（失败），Ci（补偿），…，C2，C1。