【高数定积分求解旋转体体积】 —— （上）高等数学|定积分|柱壳法|学习技巧

发布时间：2023年12月24日

🌈个人主页:?Aileen_0v0
🔥热门专栏:?华为鸿蒙系统学习|计算机网络|数据结构与算法
💫个人格言:"没有罗马,那就自己创造罗马~"

Shell method

Setting up the Integral

Computing volumes for solids of revolution using cylindrical shells（利用柱壳法计算旋转体体积）:

Shell method

柱壳法对于旋转固体体积的计算公式如下：

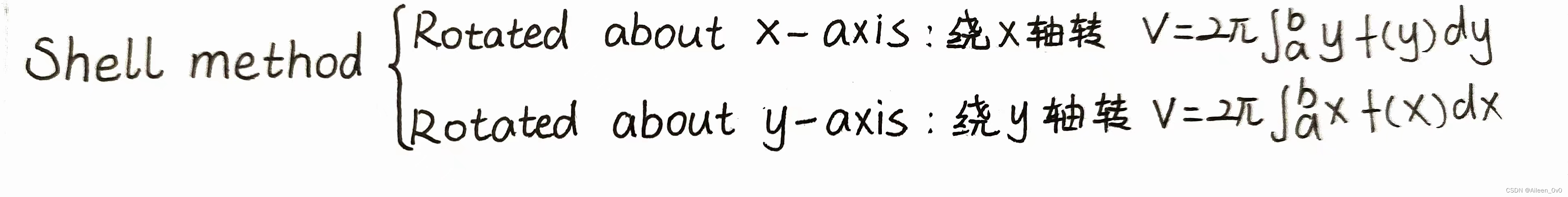
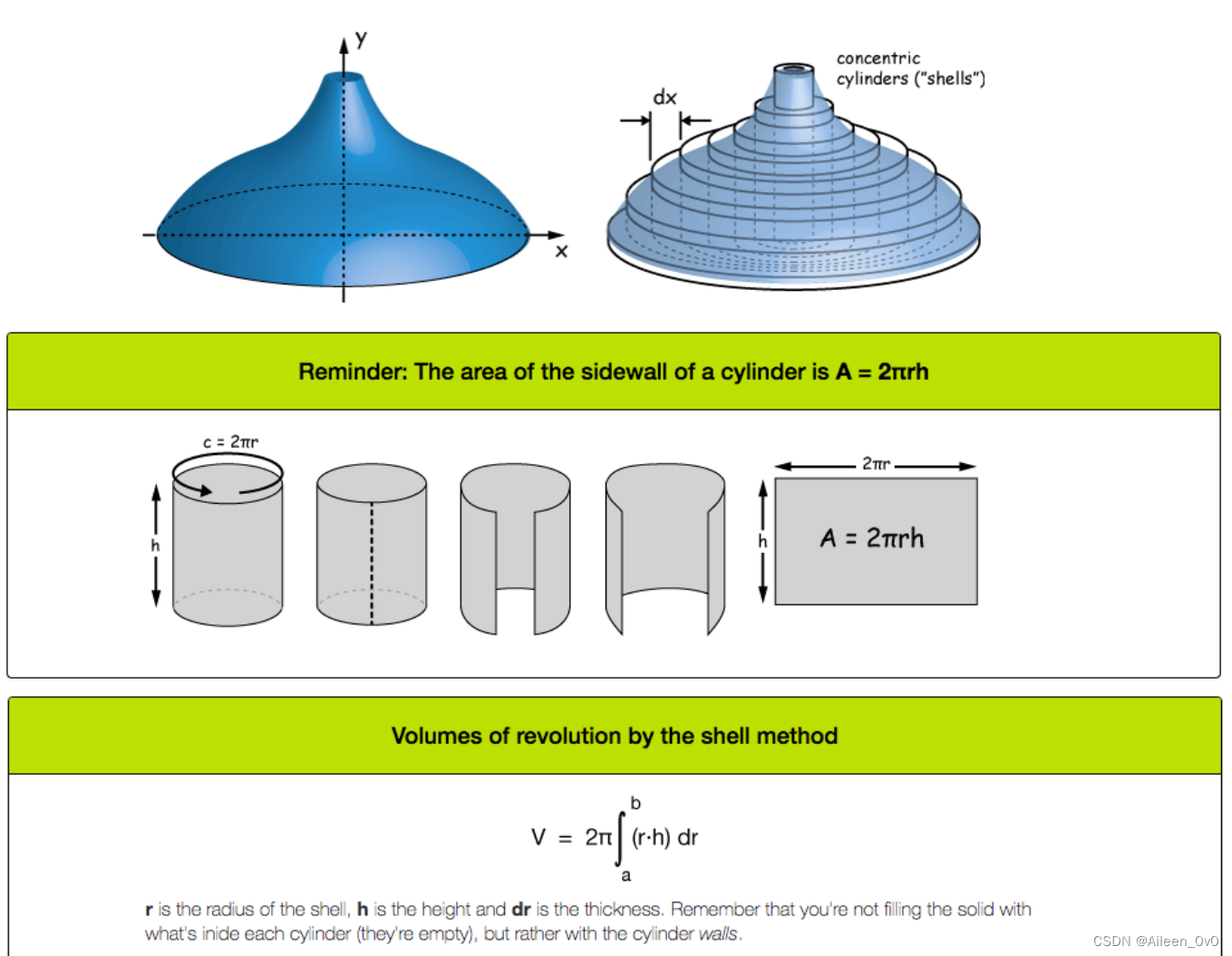Setting up the Integral

? Keypoints:

1. When using cylindrical shells, you integrate with respect to the variable that is perpendicular to the axis of rotation.(使用柱壳法时，可以相对于垂直于旋转轴的变量进行积分)

2. The integral can be set up as 2π ∫(a to b) r(x) h(x) dx or 2π ∫(c to d) r(y) h(y) dy , depending on the orientation.

例题

Example 1:

Use the shell method to find the volume of the solid generated by revolving the shaded region about the y-axis.

Limit is 0<x<pi

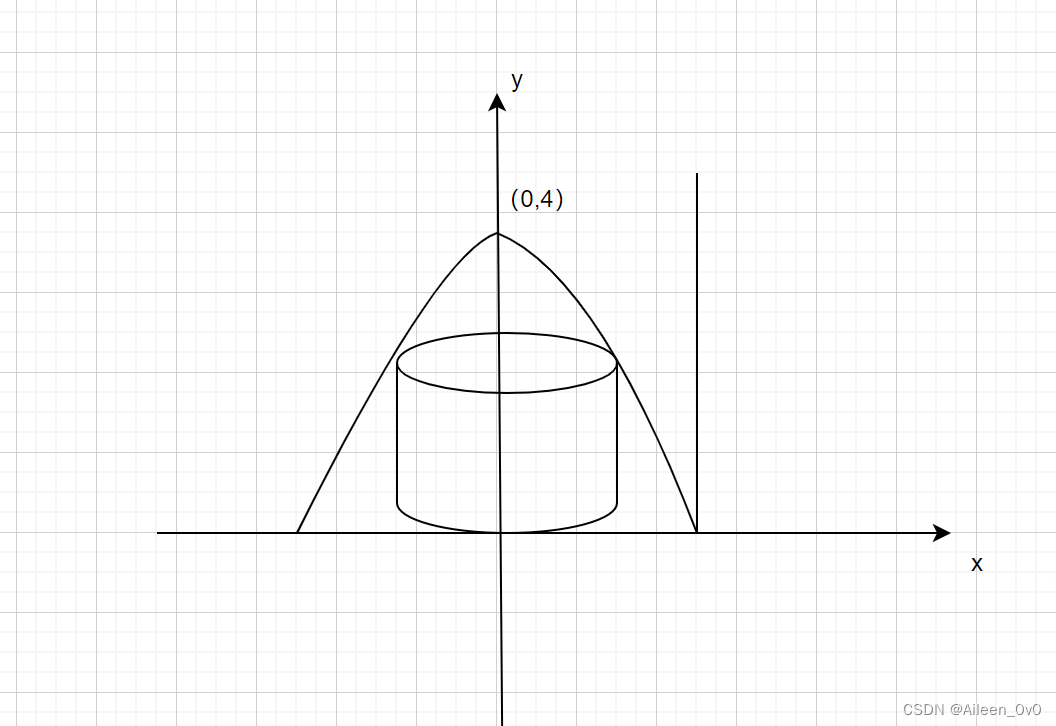
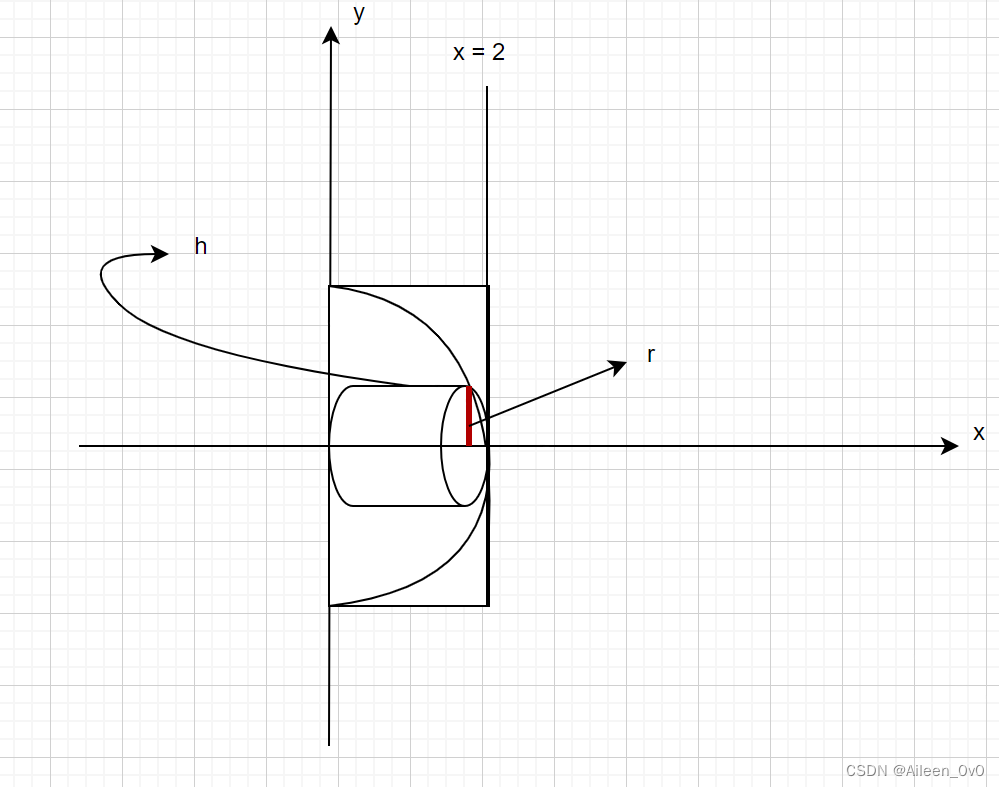
Example 2:

Use the shell method to find the volume of the solid generated by revolving the shaded region about the x-axis.

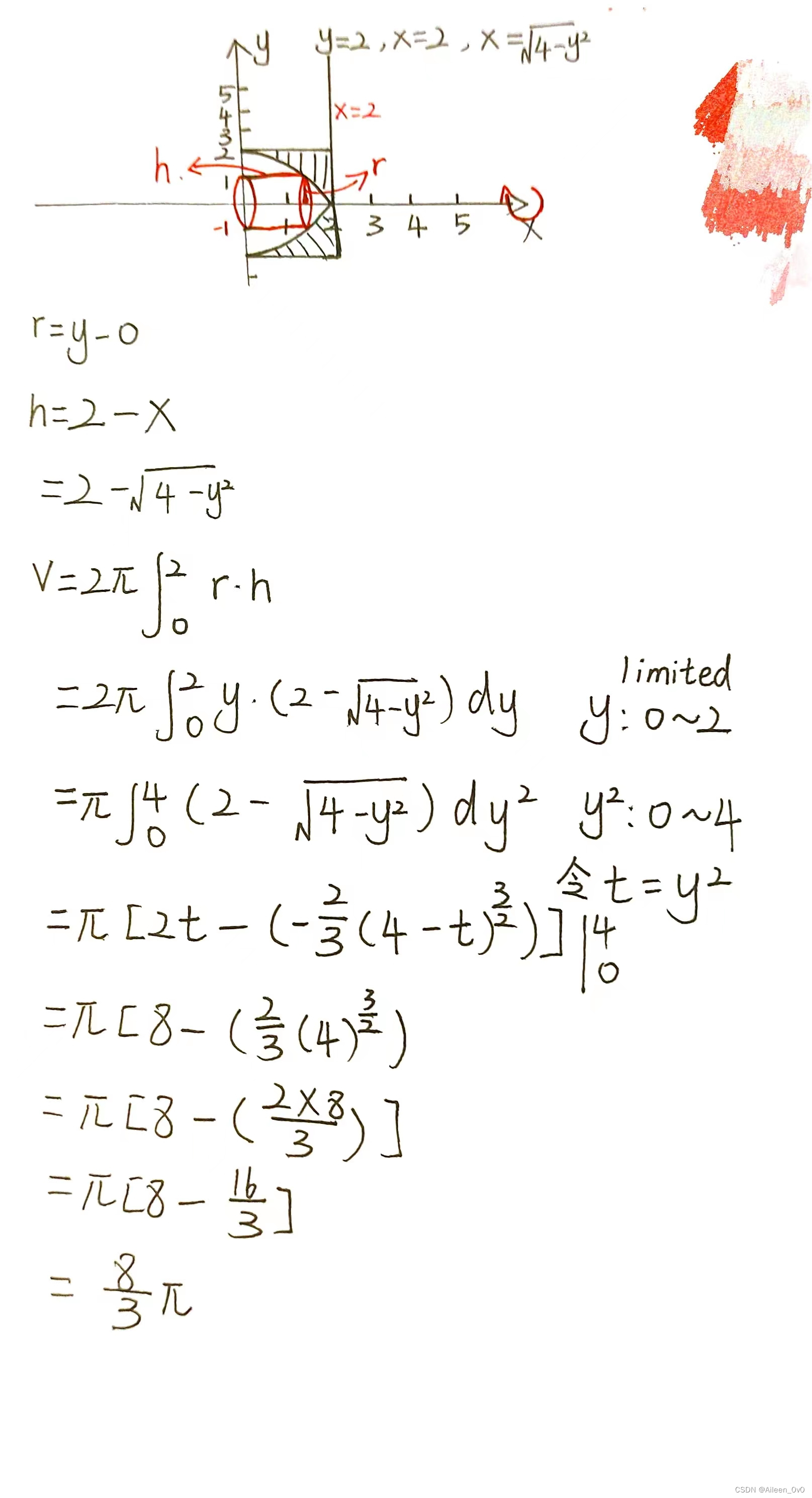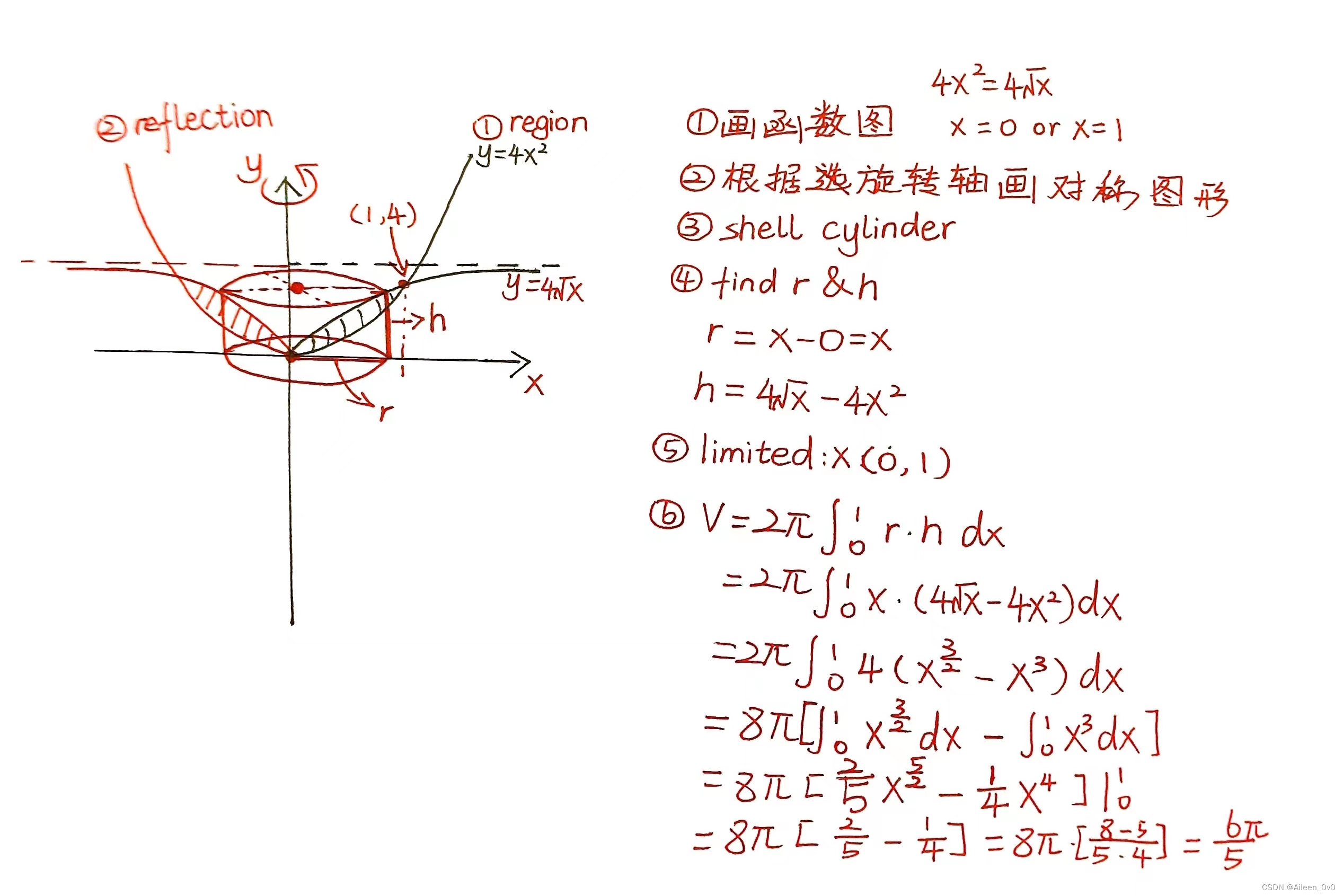
Example 3:

Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and lines about the y-axis.

文章来源:https://blog.csdn.net/Aileenvov/article/details/135171104
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！