2043杨辉三角(C语言)
发布时间:2023年12月17日
目录
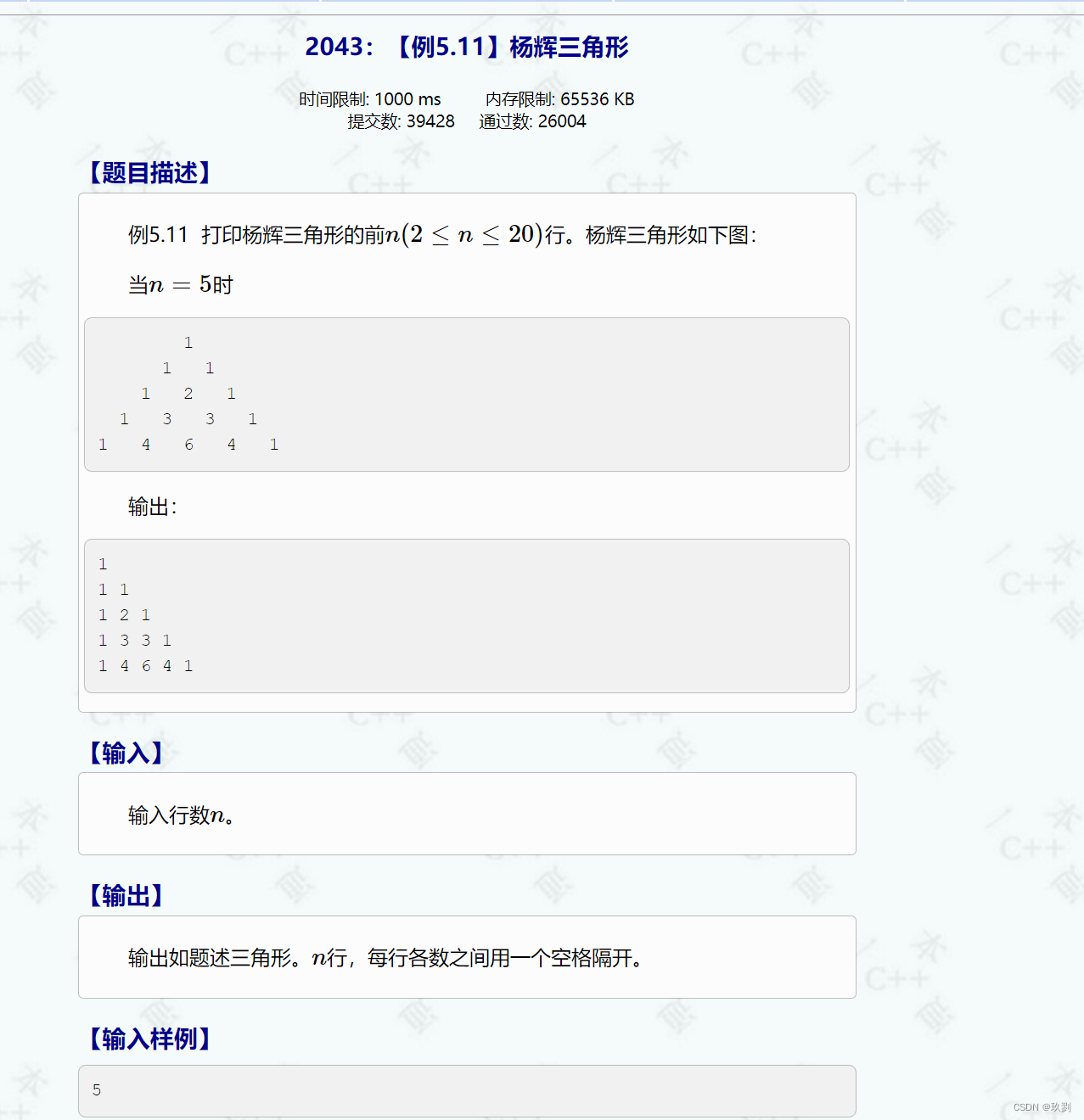
一:题目
二:思路分析
1.通过杨辉三角,不难发现中间的数等于肩头两个数之和

2.但是当我们的输出结果,与杨辉三角的形式有所不同,但是我们可以找到与杨辉三角相似的规律,即一个数等于上面的数和上面数的右边的的数的和(arr[i][j] = arr[i-1][j]+arr[i-1][j-1])

3.这是又出现一个问题,如何用代码实现呢?我们只是找到了规律,但是如何应用规律呢?我们怎么赋值呢?
不难看出第一列和最后一个数都是1,那我们要把这两种情况单独拿出来讨论,将它们赋值为1吗?
这稍微有一点麻烦。
这时,不妨看一下我对杨辉三角第一行和第二行的理解,将它们理解为第一行的两边还有一个未显示的0,第二行的1是由第一行的1+0得到的,同理假设我们求的是五行杨辉三角,那么第二行的1是由第一行的1和它右边的0相加得到的,但是如果求五行,我们创建的是5*5的二维数组的话,第一行的1是第一行开始的数,如果访问它右边的数就越界了,所以这是不妨扩建数组为6*6的。

在这个基础上,我们只要把(1,1)处的值赋为1,再带入我们找到的规律,就可以得到结果了

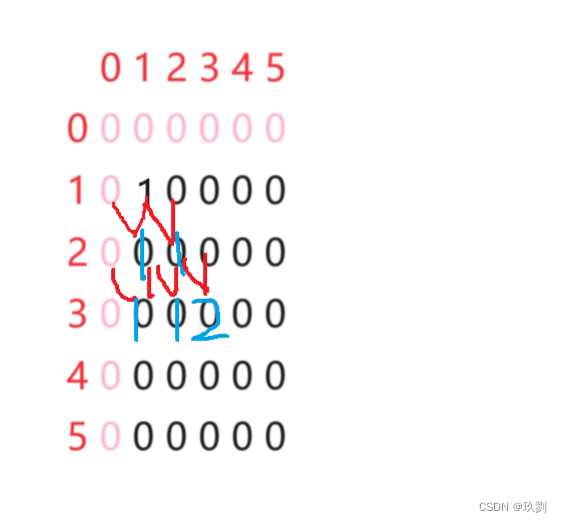
4.对于杨辉三角,第i行有i个数,所以循环时i的范围是1~n,而j的范围是1~i
三:代码
#include <stdio.h>
//2043杨辉三角
int main()
{
int n = 0;
scanf("%d", &n);
int arr[21][21] = { 0 };
int i = 0, j =0;
for (i = 1; i <= n; i++)//0~n
{
for (j = 1; j <= n; j++)
{
if (i == 1 && j == 1)
arr[i][j] = 1;
else
arr[i][j] = arr[i - 1][j] + arr[i - 1][j - 1];
}
}
for (i = 1; i <= n; i++)
{
for (j = 1; j <= i; j++)
{
printf("%d ", arr[i][j]);
}
printf("\n");
}
return 0;
}
文章来源:https://blog.csdn.net/2301_80096514/article/details/135035791
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 在线测径仪 各行业可用
- 【话题】ChatGPT 和文心一言哪个更好用
- 加载符号文件
- 云原生Kubernetes系列 | Job和CronJob使用
- jmeter如何测试websocket接口?
- 【每日面试题】Docker常见面试题精选
- vue项目hdr格式文件放在assets下rgbeloader.load获取不到问题解决
- 电机控制 相关基础概念
- C#中的Attribute详解(上)
- Miniconda3 管理 Python 环境的详细教程