【论文笔记】End-to-End Diffusion Latent Optimization Improves Classifier Guidance
Abstract
Classifier guidance为图像生成带来了控制，但是需要训练新的噪声感知模型(noise-aware models)来获得准确的梯度，或使用最终生成的一步去噪近似，这会导致梯度错位(misaligned gradients)和次优控制(sub-optimal control)。
梯度错位(misaligned gradients)：通过噪声感知模型指导生成模型时，两个模型的结构和目标不完全匹配，导致从一个模型得到的梯度并不适用于另一个模型。同样会导致梯度错位的原因还有：特征空间不同、训练数据不一致、近似方法或噪声的影响等。
次优控制(sub-optimal control)：控制不够优化或理想，分类器梯度指导图像生成，但是梯度本身不够匹配或准确， 导致控制生成图像的过程并不完全理想或者最优。
基于这种近似的缺点，本文提出了一个新颖的引导方法：Direct Optimization of Diffusion Latents(DOODL)。该方法通过优化扩散潜变量相对于预训练分类器在真实生成的像素上的梯度，利用可逆扩散过程实现内存高效的反向传播，实现即插即用的引导。
DOODL展示了更精确指导的潜力，在不同指导形式的计算和人类评估指标上优于一步分类器指导：
使用CLIP指导改进DrawBench中复杂提示的生成，使用细粒度视觉分类器扩展Stable Diffusion的词汇量，使用CLIP视觉编码器实现图像调节生成，使用美学评分网络改进图像美感。
1 Introduction
为了实现灵活又准确的模型梯度，而不适用noise-aware classifiers或近似手段，提出Direct Optimization Of Diffusion Latents (DOODL)。DOODL优化了初始扩散噪声向量，相对于全链扩散过程生成的基于模型的图像损失。
利用EDICT（最近开发出的一种可以离散反演的扩散算法），它允许与扩散步数的内存成本恒定的反向传播，以计算最终生成的像素分类器相对于原始噪声向量的梯度。这使得能够对图像像素上的任何可微损失进行高效的迭代扩散潜变量优化，并准确计算用于分类器引导的梯度。
本文演示了DOODL在多种经常使用的定量和人类评估研究中使用的引导信号上的效果。
![![[Pasted image 20240103114132 1.png]]](https://img-blog.csdnimg.cn/direct/132d45d3ac92444da771652743f126cc.png)
图1：本文的方法改进了所有测试设置中的普通分类器引导，并且展示了此类方法的新颖的功能，例如词汇扩展，实体个性化和感知审美价值改进。
第一，展示了使用DOODL的CLIP分类器引导改进了由DrawBench数据集的文本提示引导的图像生成，该数据集测试组合性和指导使用不寻常标题的能力。
第二，展示了细粒度视觉分类器扩展预训练稳定扩散模型词汇量的能力，这个能力是one-step分类器不具备的。
第三，证明了DOODL可以用于个性化实体生成（如"A dog in sunglasses"），并且对任何新的网络不进行再训练。据我们所知，这是首次做到。
最后，利用DOODL来执行一项新的任务，提高生成/真实图像的感知美学质量，希望DOODL能够为预训练的扩散模型启用和激发多种即插即用的功能。
2 Related Work
2.1 Text-to-Image Diffusion Models
Text-to-Image diffusion models，如GLIDE、DALLE-2、Imagen、Latent Diffusion、eDiffi，最近出现在图像生成的前沿。
Classifier guidance使用预训练分类器模型的梯度来指导此类生成。在每个去噪步骤之前以固定的噪声水平遍历，而不是顺序去噪。并发工作修改classifier guidance，以在继续之前细化每个噪声级别的梯度预测。
![![[Pasted image 20240103144346 1.png]]](https://img-blog.csdnimg.cn/direct/1fc01bce008046c2a5c4a3ed8e25bba5.png)
表1：基于学习的(Learning-Based)方法需要数据集和训练，但是基于引导的(Guidance-Based)方法需要预训练识别网络（在本文的设置中，是在非噪声空间中训练的）
最近在diffusion models和可逆神经网络(invertible neural networks)的焦点处有一种新的方法：EDICT，它通过算法将去噪扩散过程重新表述为可逆的过程。这项先前的工作仅关注了图像编辑的应用，没有考虑可逆神经网络或类似过程的属性。DDIM等方法理论上在离散化极限下是可逆的，但实际中无法达到这个极限。
2.2 Invertible Neural Networks (INNs)
虽然神经网络往往是非保维函数，先前已经有关于构建可逆架构的工作。此类INN的主要类别是标准化流模型，标准化流结构中“耦合层“的修改版本被纳入本工作使用的EDICT算法中。
也有工作提出了一种通过条件良好的逆问题而不是封闭式解决方案保证可逆的架构。这种架构的内存节省已被用于长序列循环神经网络并研究逆问题。
3 Background
3.1 Invertible Neural Networks w.r.t Memory
当在神经网络中使用梯度下降法来优化时，设网络参数
Ξ
=
{
ξ
p
}
p
=
1
p
=
P
\Xi=\{\xi_p\}_{p=1}^{p=P}
Ξ={ξp?}p=1p=P?，网络输入为
x
x
x，输出为
y
=
f
(
x
)
y=f(x)
y=f(x)，损失函数
c
c
c，计算导数
d
c
(
y
)
d
ξ
\frac{dc(y)}{d\xi}
dξdc(y)?并执行梯度下降从而最小化
E
D
a
t
a
c
(
y
)
=
E
D
a
t
a
c
(
f
(
x
)
)
\mathbb{E}_{Data} c(y)=\mathbb{E}_{Data} c(f(x))
EData?c(y)=EData?c(f(x))。其中
f
f
f隐含地以
Ξ
\Xi
Ξ为条件。考虑
f
f
f为
n
n
n个函数(层)的组合：
f
n
°
f
n
?
1
°
?
°
f
1
f^n\circ f^{n-1}\circ \cdots\circ f^1
fn°fn?1°?°f1。为了优化
ξ
\xi
ξ，计算第
i
i
i层参数的导数
d
c
(
y
)
d
ξ
\frac{dc(y)}{d\xi}
dξdc(y)?。设
f
k
°
f
k
?
1
°
?
°
f
j
=
F
j
k
f^k\circ f^{k-1}\circ \cdots\circ f^j=F_j^k
fk°fk?1°?°fj=Fjk?。
y
=
F
1
n
(
x
)
y=F_1^n(x)
y=F1n?(x)，那么相对于
ξ
\xi
ξ的导数可以用链式法则来计算：
d
c
(
y
)
d
ξ
=
d
c
(
F
1
n
(
x
)
)
d
ξ
=
d
c
(
F
1
n
(
x
)
)
d
F
1
n
(
x
)
?
d
F
1
n
(
x
)
d
F
1
n
?
1
(
x
)
?
d
F
1
i
(
x
)
d
F
1
i
?
1
(
x
)
?
d
F
1
i
?
1
(
x
)
d
x
\begin{align} \frac{dc(y)}{d\xi}&=\frac{dc(F_1^n(x))}{d\xi}\tag{1} \\ &=\frac{dc(F_1^n(x))}{dF_1^n(x)}\cdot\frac{dF_1^n(x)}{dF_1^{n-1}(x)}\cdots\frac{dF_1^i(x)}{dF_1^{i-1}(x)}\cdot\frac{dF_1^{i-1}(x)}{dx}\tag{2} \end{align}
dξdc(y)??=dξdc(F1n?(x))?=dF1n?(x)dc(F1n?(x))??dF1n?1?(x)dF1n?(x)??dF1i?1?(x)dF1i?(x)??dxdF1i?1?(x)??(1)(2)?
通常情况下，计算
d
c
(
y
)
d
ξ
\frac{dc(y)}{d\xi}
dξdc(y)?需要存储所有的中间激活值，这是反向传播的瓶颈。
跨处理器的网络分片减少了每个处理器的硬件内存需求，但总数仍然保持不变。
梯度检查点降低了内存成本，但是线性增加了运行时间，节省了内存。
INN可以从输出中恢复中间状态/输入，通过避免激活缓存来降低内存成本。如果Eq.1中每个
f
j
f^j
fj都是可逆的，分母项可以在向后传递期间重建。此类方法已被用来训练大型INN，其速度比不可逆的等效方法快得多。
3.2 Denoising Diffusion Models (DDMs)
图像的DDMs被训练用于预测加入图像
x
x
x的噪声
?
\epsilon
?。噪声被离散化后可以用一个集合
T
=
{
0
,
1
,
?
?
,
T
}
\mathcal{T}=\{0,1,\cdots,T\}
T={0,1,?,T}来索引：
{
α
t
}
t
=
0
T
,
α
T
=
0
,
α
0
=
1
\{\alpha_t\}_{t=0}^T,\alpha_T=0,\alpha_0=1
{αt?}t=0T?,αT?=0,α0?=1。
t
∈
T
t\in \mathcal{T}
t∈T在训练期间随机采样并和数据
x
(
i
)
x^{(i)}
x(i)（图像或自动编码表示）生成噪声样本：
x
t
(
i
)
=
α
t
x
(
i
)
+
1
?
α
t
?
(3)
x_t^{(i)}=\sqrt{\alpha_t}x^{(i)}+\sqrt{1-\alpha_t}\epsilon\tag{3}
xt(i)?=αt??x(i)+1?αt???(3)
其中
?
～
N
(
0
,
I
)
\epsilon\sim N(0,I)
?～N(0,I)。
以时间步
t
t
t和辅助信息（例如图像标题）
C
C
C为条件的DDM被训练以近似添加的噪声：
D
D
M
(
x
t
(
i
)
,
t
,
C
)
≈
?
DDM(x_t^{(i)},t,C)\approx \epsilon
DDM(xt(i)?,t,C)≈?。生成的过程中，
x
T
～
N
(
0
,
1
)
x_T\sim N(0,1)
xT?～N(0,1)采样，DDM被迭代应用，从噪声中幻化出真实图像。根据DDIM采样模型，最后生成的
x
0
x_0
x0?等同于
S
S
S个去噪函数的复合函数：在条件
C
C
C和步数
t
t
t上应用
Θ
\Theta
Θ。令
Θ
(
x
,
t
,
C
)
\Theta(x,t,C)
Θ(x,t,C)为
Θ
(
t
,
C
)
(
x
)
\Theta_{(t,C)}(x)
Θ(t,C)?(x)，于是有：
x
0
=
[
Θ
(
0
,
C
)
°
Θ
(
1
,
C
)
°
?
°
Θ
(
T
,
C
)
]
(
x
T
)
(4)
x_0=[\Theta_{(0,C)}\circ\Theta_{(1,C)}\circ\cdots\circ \Theta_{(T,C)}](x_T)\tag{4}
x0?=[Θ(0,C)?°Θ(1,C)?°?°Θ(T,C)?](xT?)(4)
3.2.1 Classifier Guidance
除了
C
C
C以外，其他引导信号也可以引导生成图像。最重要的例子：classifier guidance将估计像素上的损失梯度(
c
c
l
f
c_{clf}
cclf?，来自分类器网络
Φ
\Phi
Φ)合并到噪声预测中。
从理论角度来看，这通常是对数条件概率
?
log
?
p
Φ
(
y
∣
x
t
)
\nabla \log p_\Phi(y|x_t)
?logpΦ?(y∣xt?)的梯度。合并分类器指导有两种主要方法：
- 一个noise-aware classifier经过训练可以直接用于中间（噪声） x t x_t xt?，并将 ? x t c c l f ( x t ) \nabla_{x_t} c_{clf}(x_t) ?xt??cclf?(xt?)纳入到去噪预测当中。训练噪声感知模型是有效的，但由于计算费用和数据可用性而通常不可行。这导致公开的噪声感知模型非常少。
- x 0 x_0 x0?是通过 Θ ( t , C ) \Theta_{(t,C)} Θ(t,C)?来近似的，合并的梯度是 ? x t c c l f ( x 0 ? ) \nabla_{x_t} c_{clf}(x_0^*) ?xt??cclf?(x0??)，其中 x 0 ? x_0^* x0??是一个单步近似，用 Θ ( t , C ) \Theta_{(t,C)} Θ(t,C)?来替换Eq.3中的 ? \epsilon ?。虽然可以使用标准模型，但是梯度是根据近似的 x 0 x_0 x0?来计算的，可能会导致 d c c l f ( x t ) x 0 \frac{dc_{clf}(x_t)}{x_0} x0?dcclf?(xt?)?无法对齐。
3.2.2 Exact Inversion of the Diffusion Process
最近，EDICT，一个离散的(时间步进)扩散模型的精确可逆变体被提出。EDICT对潜在对
(
x
t
,
y
t
)
(x_t,y_t)
(xt?,yt?)进行操作，而不是单个变量。
初始化
x
T
=
y
T
～
N
(
0
,
I
)
x_T=y_T\sim N(0,I)
xT?=yT?～N(0,I)，然后使用反向扩散过程迭代去噪：
x
t
i
n
t
e
r
=
a
t
?
x
t
+
b
t
?
Θ
(
t
,
C
)
(
y
t
)
y
t
i
n
t
e
r
=
a
t
?
y
t
+
b
t
?
Θ
(
t
,
C
)
(
x
t
i
n
t
e
r
)
x
t
?
1
=
p
?
x
t
i
n
t
e
r
+
(
1
?
p
)
?
y
t
i
n
t
e
r
y
t
?
1
=
p
?
y
t
i
n
t
e
r
+
(
1
?
p
)
?
x
t
?
1
\begin{align} x_t^{inter}&=a_t\cdot x_t+b_t\cdot\Theta_{(t,C)}(y_t) \\ y_t^{inter}&=a_t\cdot y_t+b_t\cdot\Theta_{(t,C)}(x_t^{inter}) \\ x_{t-1}&=p\cdot x_t^{inter}+(1-p)\cdot y_t^{inter} \\ y_{t-1}&=p\cdot y_t^{inter}+(1-p)\cdot x_{t-1}\tag{5} \end{align}
xtinter?ytinter?xt?1?yt?1??=at??xt?+bt??Θ(t,C)?(yt?)=at??yt?+bt??Θ(t,C)?(xtinter?)=p?xtinter?+(1?p)?ytinter?=p?ytinter?+(1?p)?xt?1??(5)?
其中
(
a
t
,
b
t
)
(a_t,b_t)
(at?,bt?)是与时间有关的系数，
p
∈
[
0
,
1
]
p\in[0,1]
p∈[0,1]是用于减轻潜在漂移的混合系数。
直观地说，整个过程，首先根据对方的状态更新
x
x
x和
y
y
y序列，然后可逆地将它们”平均“在一起。
上述方程允许线性解来反转它们，定义逆过程：
y
t
+
1
i
n
t
e
r
=
(
y
t
?
(
1
?
p
)
?
x
t
)
/
p
x
t
+
1
i
n
t
e
r
=
(
x
t
?
(
1
?
p
)
?
y
t
+
1
i
n
t
e
r
)
/
p
y
t
+
1
=
(
y
t
+
1
i
n
t
e
r
?
b
t
+
1
?
Θ
(
t
+
1
,
C
)
(
x
t
+
1
i
n
t
e
r
)
)
/
a
t
+
1
x
t
+
1
=
(
x
t
+
1
i
n
t
e
r
?
b
t
+
1
?
Θ
(
t
+
1
,
C
)
(
y
t
+
1
)
)
/
a
t
+
1
\begin{align} y_{t+1}^{inter}&=(y_t-(1-p)\cdot x_t)/p \\ x_{t+1}^{inter}&=(x_t-(1-p)\cdot y_{t+1}^{inter})/p \\ y_{t+1}&=(y_{t+1}^{inter}-b_{t+1}\cdot\Theta_{(t+1,C)}(x_{t+1}^{inter}))/a_{t+1} \\ x_{t+1}&=(x_{t+1}^{inter}-b_{t+1}\cdot\Theta_{(t+1,C)}(y_{t+1}))/a_{t+1} \tag{6} \end{align}
yt+1inter?xt+1inter?yt+1?xt+1??=(yt??(1?p)?xt?)/p=(xt??(1?p)?yt+1inter?)/p=(yt+1inter??bt+1??Θ(t+1,C)?(xt+1inter?))/at+1?=(xt+1inter??bt+1??Θ(t+1,C)?(yt+1?))/at+1??(6)?
我们在DOODL中使用这个构造，并在5.3节中使用Eq.6来编码图像
x
0
x_0
x0?为潜变量
x
T
x_T
xT?。
4 Direct Optimization of Diffusion Latents
我们的目标是客服classifier guidance在3.2.1节中讨论的短板。具体地，我们的方法有以下优点：
- 不需要重新训练/微调一个已经存在的预训练好的分类模型
- 计算相对于真实输出的梯度，而不是单步近似
- 在语义上有意义的方式合并梯度，而不是对抗式扰动
特别强调最后一点，相对于像素的梯度可以满足分类器损失，同时不会在感知上改变图像的内容。这与GAN中的潜在优化等技术相反，其中解码器提供的正则化意味着优化发生在扰动通常会导致满足所需目标的感知上有意义的变化的空间中。
这项工作中，我们的目标是直接优化扩散潜势(diffusion latents)，这在文献中第一次出现。
由Eq.4可知，针对
x
0
x_0
x0?的期望结果对
x
T
x_T
xT?进行优化是微不足道的，Eq.1中有一个闭式表达式
d
x
0
x
T
\frac{dx_0}{x_T}
xT?dx0??。
然而， 由于激活缓存，因为
Θ
\Theta
Θ的
T
T
T次应用，原始内存成本与DDIM采样步骤的数量呈线性关系。当
S
=
50
S=50
S=50时，对于最先进的扩散模型来说，内存成本接近1TB，对于大多数用途来说都是不切实际的。
梯度检查点(Gradient checkpointing)以内存换取计算复杂性，如果内存成本保持不变，则每次向后传递的计算复杂性都会增加
S
S
S倍。
我们从3.1节的INN汲取灵感，在可行的运行时间内优化 x T x_T xT?相对 x 0 x_0 x0?的标准。在Eq.4中使用可逆的 Θ ( i , C ) \Theta_{(i,C)} Θ(i,C)?，即可在反向过程期间重建一个中间过程，仅使用相对于 T T T一个常数数量的 Θ \Theta Θ，在不牺牲运行时间的情况下规避过高的内存成本。
我们将最近研究发现的EDICT作为可逆的反向扩散过程，其允许在常数内存空间内实现对 x t x_t xt?的优化。给定条件 C C C，基于可微模型的成本函数 c c c，一个潜在抽样 x T ( 0 ) x_T^{(0)} xT(0)?，执行EDICT生成过程(50步， p = 0.93 p=0.93 p=0.93，Stable Diffusion v1.4)，产生初始输出 f ( x T ( 0 ) ) = x 0 ( 0 ) f(x_T^{(0)})=x_0^{(0)} f(xT(0)?)=x0(0)?，用于计算损失 c ( x 0 ( 0 ) ) c(x_0^{(0)}) c(x0(0)?)和相应的梯度 ? x t c ( f ( x T ( 0 ) ) ) \nabla_{x_t} c(f(x_T^{(0)})) ?xt??c(f(xT(0)?))。然后这个梯度可以被用于对 x T ( 0 ) x_T^{(0)} xT(0)?执行梯度下降优化步骤。
我们通过几种关键的方式修改普通梯度下降，以获得满足指导标准的逼真图像。
在每个优化步骤之后，EDICT”完全噪声“潜在对
x
T
(
j
)
x_T^{(j)}
xT(j)?和
y
T
(
j
)
y_T(j)
yT?(j)（来自Eq.5~6）被一起平均并重新归一化为初始抽取的
x
T
(
0
)
x_T^{(0)}
xT(0)?。平均可以防止潜变量漂移，从而避免降低质量。归一化到原始范数可以保持”高斯壳(gaussian shell)“上的潜变量，保持扩散模型上的分布。
我们还对生成的 ( x 0 , y 0 ) (x_0,y_0) (x0?,y0?)执行多样裁剪(multi-crop)数据的增强，对每个图像采样进行16次裁剪。采用的动量 η = 0.9 \eta=0.9 η=0.9。我们发现Nesterov momentum没有很多用处，最后，为了提高输出图像的稳定性和真实性，每次更新我们对 g g g进行了逐元素裁剪，幅度为 1 0 ? 3 10^{-3} 10?3，扰动 x T x_T xT?在 N ( 0 , 1 0 ? 4 ? I ) \mathcal{N}(0,10^{-4}\cdot I) N(0,10?4?I)上采样。
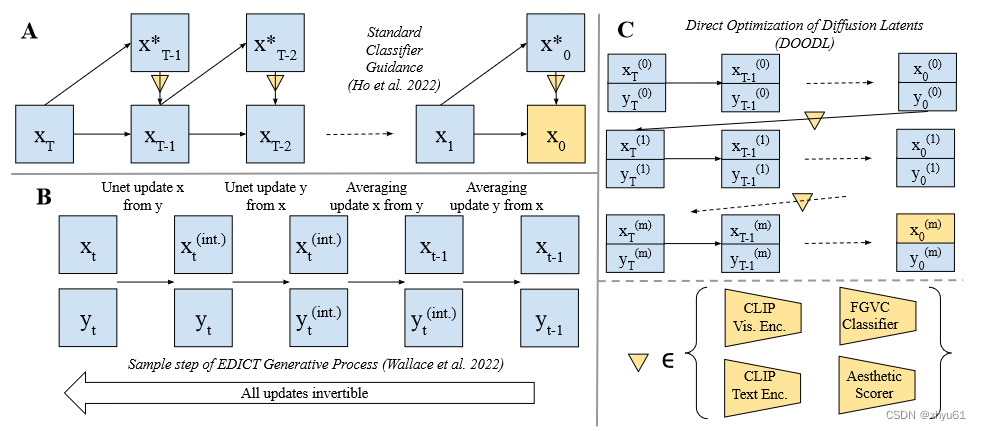
图3：
- A：基础的classifier guidance。在每一步 t t t中，通过一步去噪近似 x 0 x_0 x0?，计算相对于这次生成 x 0 x_0 x0?的逐像素的损失。该损失的梯度被纳入后续的扩散步骤中。
- B：EDICT。扩散过程的可逆变体，允许在整个链中进行反向传播，而无需额外的内存成本。
- C：DOODL。我们利用EDICT，展示了针对最终生成物计算的模型损失可以被直接用于优化完整的噪声
x
T
x_T
xT?。
图中 ? \nabla ?表示基于可微模型的损失的梯度计算。
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！