神经网络 —— 模拟人脑的计算方式

神经网络能够反映人类大脑的行为，允许计算机程序识别模式，以及解决人工智能、机器学习和深度学习领域的常见问题。

• 人类发明的灵感来源有很多都是来自大自然，神经网络同样如此。人工神经网络是一种类似于人类神经网络的信息处理技术。但事实上，神经网络有很多种，虽然他们都统称为“神经网络”，但每种神经网络都各有其内部的机制与原理以及不同的神经网络采用不同的网络模型和学习机制。
• 神经网络反映人类大脑的行为，允许计算机程序识别模式，以及解决人工智能、机器学习和深度学习领域的常见问题。

2.1 生物神经网络的基本原理

在生物神经网络中，每个神经元与其他神经元通过突触进行连接。

• 人，无疑是有智能的。如果想让“人造物”具备智能，模仿人类是最朴素不过的方法论了。自然地，人们同样期望研究生物大脑的神经网络，然后效仿之，从而获得智能。人工神经网络（Artificial Neural Network, ANN）便是其中的研究成果之一。而人工神经网络的性能好坏，高度依赖于神经系统的复杂程度，它通过调整内部大量“简单单元”之间的互连权重达到处理信息的目的，并具有自学习和自适应的能力。
• 而上述定义中的“简单单元”，就是神经网络中的最基本元素——神经元（Neuron）模型。如图所示，在生物神经网络中，每个神经元与其他神经元通过突触进行连接，神经元在工作的过程中，其他神经元的信号（输入信号）通过树突传递到细胞体（也就是神经元本体）中，细胞体把从其他多个神经元传递进来的输入信号进行合并加工，然后再通过轴突前端的突触传递给别的神经元。

神经元之间的信息传递，属于化学物质的传递。

• 神经元之间的信息传递，属于化学物质的传递。当神经元“兴奋”时，就会向与它相连的神经元发送化学物质（神经递质，Neurotransmitter），从而改变这些神经元的电位。如果某些神经元的电位超过了一个阈值，相当于达到了阈值函数器的阈值，那么它就会被“激活”，在也就是“兴奋”起来，接着向其他神经元发送化学物质，一层接着一层传播。

2.2 M-P神经元模型

2.2.1 基本概念

M-P神经元模型实际上是对单个神经元的一种建模。

• 在这一模型中，神经元接收来自各个其他神经元传递过来的输入信号。这些信号的表达，通常通过神经元之间连接的权重（Weight）大小来表示，神经元将接收到的输入值按照某种权重叠加起来，叠加起来的刺激强度，可如图用公式表示
• 从公式可以看出，当前神经元按照某种“轻重有别”的方式，汇集了所有其他外联神经元的输入，并将其作为一个结果输出。但这种输出，并非直接输出，而是与当前神经元的阈值进行比较，然后通过激活函数（Activation Function）向外表达输出，在概念上这就叫感知机（Perceptron），其模型可用一下公式二来表示： 在这里， 就是所谓的“阈值（Threshold）”， 就是激活函数， 就是最终的输出。可以看出M-P模型就是一个加权求和再激活的过程，能够完成线性可分的分类问题。

2.2.2 代码实现

以经典乳腺癌为例

In [18]

#导入需要的包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import sklearn.datasets
from sklearn.metrics import accuracy_score #以准确率为评价指标
from sklearn.model_selection import train_test_split #用来分割数据集
#导入数据集
from sklearn.datasets import load_breast_cancer
#分离特征和标签
# 1表示良性，0表示恶性
breast_cancer = sklearn.datasets.load_breast_cancer()
data = pd.DataFrame(breast_cancer.data,columns=breast_cancer.feature_names)
data['class'] = breast_cancer.target
data['class'].value_counts()
X = data.drop('class',axis=1)
y = data['class']
#数据集划分
#划分数据集和测试集，测试集的大小为总体数据的15%。设置stratify=y
#按照数据集中y的比例分配给train和test，使得train和test中各类别数据的比例与原数据集的比例一致。通常在数据集的分类分布不平衡的情况下会用到stratify。
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.15, stratify=y, random_state=0)
#M—P神经元模型仅能把0或1作为输入，所以我们要把数据进行处理，划分为0和1两类。
X_binarise_train =X_train.apply(pd.cut, bins=2, labels=[1,0])
X_binarise_test = X_test.apply(pd.cut, bins=2, labels=[1,0])
#获取value，用数组进行计算
X_binarise_train = X_binarise_train.values
X_binarise_test = X_binarise_test.values
#构建M-P神经元类
class MPNeuron:
    def __init__(self):
        self.b = None
    
    def model(self,x):
        return (sum(x) >= self.b)
    
    def predict(self,X):
        y = []
        for x in X:
            y.append(self.model(x))
        return np.array(y)
    
    def fit(self,X,y):
        accuracy = {}
        for b in range(X.shape[1] + 1):
            self.b = b
            y_pred = self.predict(X)
            accuracy[b] = accuracy_score(y_pred,y)
            
        best_b = max(accuracy, key = accuracy.get)
        self.b = best_b
        #打印最佳b值和最高准确率
        print('best_b:', best_b)
        print('best_accuracy:', accuracy[best_b])

#用M-P神经元训练，机器学习叫作fit，深度学习叫作train
mp_neuron = MPNeuron()
mp_neuron.fit(X_binarise_train,y_train)
#打印accuracy_score
w = mp_neuron.predict(X_binarise_test)
accuracy_score(w,y_test)

2.3 激活函数

2.3.1 基本概念

阶跃函数 — 可以将神经元输入值与阈值的差值映射为输出值1或0.若差值大于等于零则输出1，对应兴奋；若差值小于零则输出0，对应抑制。

• 前面提到了，神经元的工作模型存在“激活（1）”和“抑制（0）”两种状态的跳变，那么理想的激活函数就应该是图中所示的阶跃函数（Step Function，阶跃函数是一种特殊的连续时间函数，是一个从0跳变到1的过程，属于奇异函数）。阶跃函数可以将神经元输入值与阈值的差值映射为输出值1或0；若差值大于等于零则输出1，对应兴奋；若差值小于零则输出0，对应抑制。
• 但事实上，在实际使用中，阶跃函数具有不光滑、不连续等众多不“友好”的特性，使用的并不广泛。说它“不友好”的原因是，在神经网络中训练网络权重时，通常依赖对某个权重求偏导、寻极值，而不光滑、不连续等通常意昧着该函数无法“连续可导”。

S型函数（sigmoid函数）— 无论输入值的范围有多大，这个函数都可以将输出挤压在范围（0，1）之内。

• 因此，我们通常用S型函数函数来代替阶跃函数，最常用的S型函数为sigmoid函数，如图中所示。在sigmoid函数中，无论输入值 的范围有多大，这个函数都可以将输出挤压在范围（0，1）之内，因此此这个函数又被称为“挤压函数（Squashing Function）”。这样，如果输入的值在（0，0.5）之间，那么对于Sigmoid函数，则输出大于0.5小于1，对应兴奋；如果输入值在（-0.5，0）之间，那么输出则小于0.5大于0，对应抑制。
• 既然如此，我们又应该怎样理解激活函数呢？其实从生活中就可以找到相似的影子。比如有一个父亲为了奖励他的孩子，对他说如果下次期末总成绩90分以上就奖励100元，不到90分就没有奖励。现在我们把这一过程抽象为一个M-P神经元模型。父亲最终会有两个状态，一个是奖励100元（激活），一个是没有奖励（抑制）。输入的 、 、到 等因素为孩子的表现，比如 代表孩子今天有没有认真听课， 代表孩子有没有认真完成作业， 代表孩子考试有没有认真计算。这些表现因素乘以各自的权重相加就是孩子的期末总成绩，如果总成绩没有超过父亲奖励的阈值，则最终相减的结果小于0，经过阶跃激活函数后值为0，代表父亲处于抑制状态，也就是没有奖励。但在第二次，孩子学习更加刻苦，考试过程中也特别认真，最后乘以各因素权重后的和超过了父亲的奖励阈值，即超过了90分，则最终相减的结果大于0，此时经过阶跃激活函数后的值为1，代表父亲处于激活状态，于是奖励给了孩子100元。 这便是激活函数以及整个M-P神经元模型的基本原理。

2.3.2 代码实现

阶跃函数

In [2]

import numpy as np  
import matplotlib.pyplot as plt  
def step_function(x):  
    return np.where(x >= 0, 1, 0)   # 如果输入值大于等于0，则输出1，否则输出0
x = np.linspace(-2, 2, 1000)  # 创建一个从-2到2的等差数列，包含1000个元素  
y = step_function(x)  
plt.figure(figsize=(8, 6))  # 创建一个8x6大小的新图形  
plt.plot(x, y)  
plt.title('Step Function')  
plt.xlabel('x')  
plt.ylabel('y')  
plt.grid(True)  # 添加网格线  
plt.axis('on') #显示坐标轴
plt.show()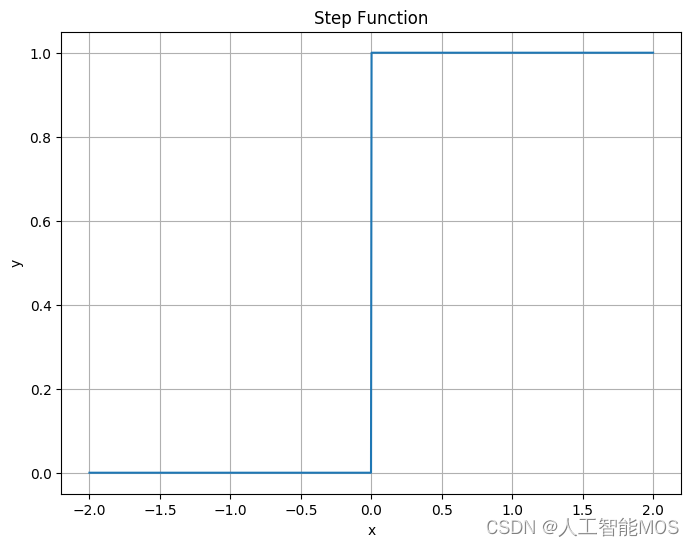

<Figure size 800x600 with 1 Axes>

S型函数

In [16]

# 导入numpy库，用于进行数学计算  
import numpy as np  
# 导入matplotlib库，用于绘制图形  
import matplotlib.pyplot as plt   
# 定义sigmoid函数，接受一个参数x  
def sigmoid(x):  
    # 返回1 / (1 + np.exp(-x))的结果，np.exp(-x)计算e的-x次方  
    return 1 / (1 + np.exp(-x))   
# 使用numpy的linspace函数在-10和10之间创建一个等间距的点集，结果存储在x中  
x = np.linspace(-10, 10, 1000)  
# 计算每个点的sigmoid值并存储在y中  
y = sigmoid(x)   
# 使用matplotlib的plot函数将这个函数绘制出来  
plt.plot(x, y)  
# 设置图形的标题为"Sigmoid Function"  
plt.title("Sigmoid Function")  
# 设置x轴的标签为"x"  
plt.xlabel("x")  
# 设置y轴的标签为"y"  
plt.ylabel("y")  
# 添加网格线  
plt.grid(True)  
# 显示图像  
plt.show()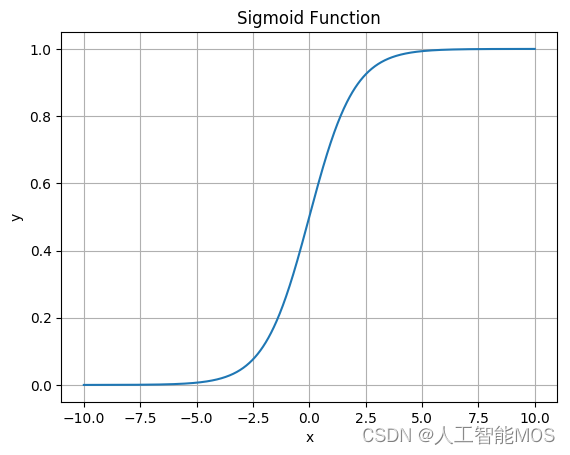

<Figure size 640x480 with 1 Axes>