C#，楔子数（Sphenic Number）的暴力算法与高效算法源代码

楔子数（Sphenic Number）来自于一个题目：

Schoolboy Vasya is interested in the problem of distinguishing prime numbers. He has decided to develop his own testing method for it. Unfortunately, the new algorithm has one deficiency – it yields false positive outputs in case with so-called sphenic numbers. For those who does not know: sphenic number is the product of exactly three distinct prime numbers. Help Vasya write a program to distinguish sphenic numbers.

译文：

小学生瓦西亚对区分素数的问题很感兴趣。他决定开发自己的测试方法。不幸的是，新算法有一个缺陷——在使用所谓的sphenic数的情况下，它会产生假阳性输出。对于那些不知道的人来说：Sphenic Number是三个不同素数的乘积。帮助Vasya编写一个程序来计算（分解）sphenic number。

Define：

????????Sphenic Number = Prime1 * Prime2 * Prime3

Where:

????????Prime1 != Prime2

????????Prime2 != Prime3

一、运算效果

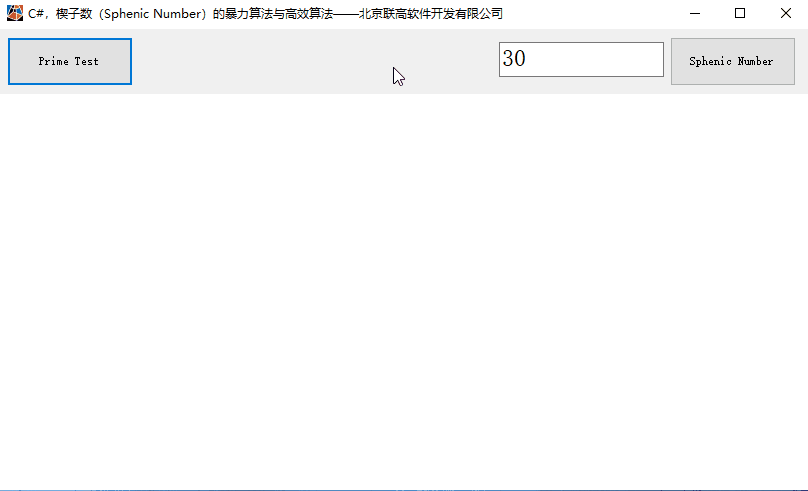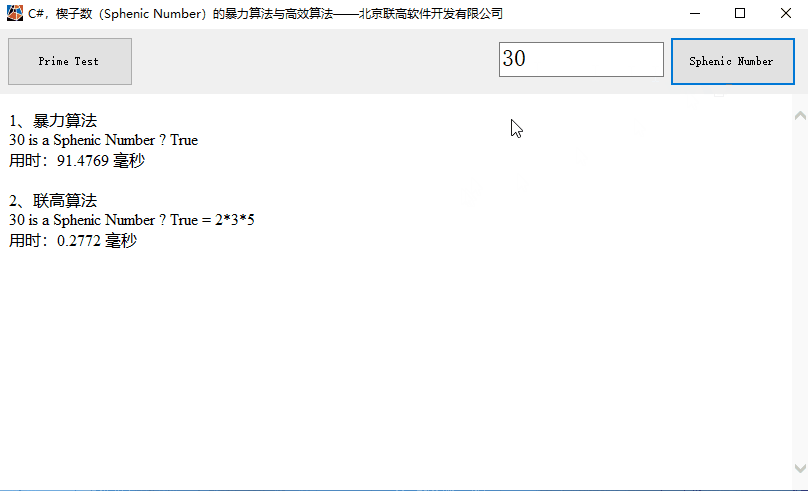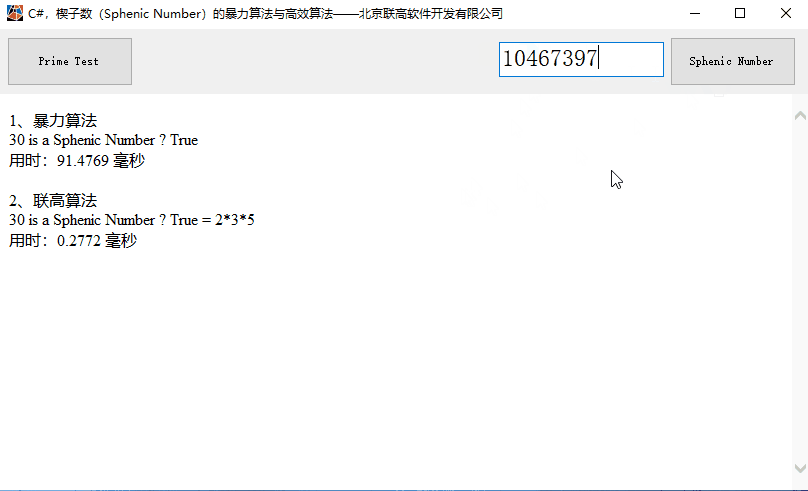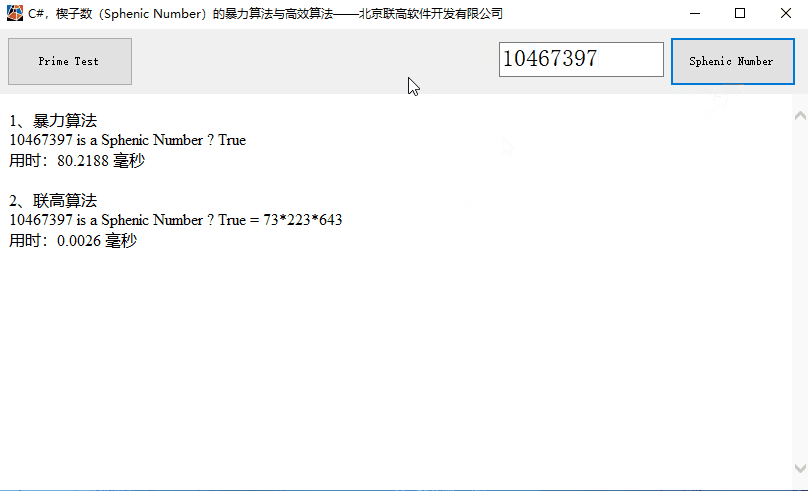
二、暴力求解算法源代码

/// <summary>
/// 最大质数
/// </summary>
private static int primeMax { get; set; } = 10467397 / 6;
/// <summary>
/// 质数总数
/// </summary>
private static int primeCount { get; set; } = 0;
/// <summary>
/// 质数筛（数组）
/// </summary>
private static int[] primeArray { get; set; } = new int[primeMax + 10];

/// <summary>
/// 构造质数（筛）
/// </summary>
public static void SieveInitialize()
{
	primeCount = 0;
	int[] visitArray = new int[primeMax + 10];
	for (int i = 2; i < primeMax; i++)
	{
		if (visitArray[i] == 0)
		{
			primeArray[primeCount++] = i;
			for (int j = 1; j * i <= primeMax; j++)
			{
				visitArray[j * i] = 1;
			}
		}
	}
}

/// <summary>
/// 暴力求解 x 是不是 楔子数
/// </summary>
/// <param name="x"></param>
/// <returns></returns>
public static bool IsSphenicOriginal(int x)
{
	int i = 0;
	int count = 0;
	for (i = 0; i < primeCount && x > 1; i++)
	{
		if ((x % primeArray[i]) == 0)
		{
			count++;
			x /= primeArray[i];
		}
		if ((x % primeArray[i]) == 0)
		{
			break;
		}
	}
	if (count == 3 && x == 1) // && !(i < cur && n > 1)
	{
		return true;
	}
	return false;
}

三、高效算法

/// <summary>
/// 哈希表
/// </summary>
private Hashtable sphenicHash { get; set; } = new Hashtable();
/// <summary>
/// 保存全部楔子数的列表
/// </summary>
private List<int> sphenicNumbers { get; set; } = new List<int>();
/// <summary>
/// 表达式
/// </summary>
private List<string> sphenicExpressions { get; set; } = new List<string>();

/// <summary>
/// 构造函数
/// </summary>
/// <param name="max"></param>
public SphenicNumber(int max = 100)
{
	List<int> ps = PrimeList(max);
	for (int i = 0; i < ps.Count - 2; i++)
	{
		for (int j = i + 1; j < ps.Count - 1; j++)
		{
			for (int k = j + 1; k < ps.Count; k++)
			{
				int v = ps[i] * ps[j] * ps[k];
				sphenicNumbers.Add(v);
				sphenicExpressions.Add(ps[i] + "*" + ps[j] + "*" + ps[k]);
				if (!sphenicHash.ContainsKey(v))
				{
					sphenicHash.Add(v, sphenicHash.Count);
				}
			}
		}
	}
}

/// <summary>
/// 总数
/// </summary>
public int Count
{
	get
	{
		return sphenicNumbers.Count;
	}
}

/// <summary>
/// 提取第 index 个楔子数
/// </summary>
/// <param name="index"></param>
/// <returns></returns>
public int this[int index]
{
	get
	{
		return sphenicNumbers[index];
	}
}

/// <summary>
/// 提取全部楔子数
/// </summary>
/// <returns></returns>
public List<int> ToList()
{
	return (sphenicNumbers);
}

/// <summary>
/// 提取全部表达式列表
/// </summary>
/// <returns></returns>
public List<string> ToExpressionList()
{
	return (sphenicExpressions);
}

/// <summary>
/// 构造不超过 x 的全部质数列表
/// </summary>
/// <param name="x"></param>
/// <returns></returns>
private List<int> PrimeList(int x = 100)
{
	List<int> list = new List<int>();
	list.Add(2);
	list.Add(3);
	for (int j = 4; j <= x; j++)
	{
		bool isprime = true;
		for (int i = 2; (i * i) <= j; i++)
		{
			if ((j % i) == 0)
			{
				isprime = false;
				break;
			}
		}
		if (isprime)
		{
			list.Add(j);
		}
	}
	return list;
}

/// <summary>
/// 检验 x 是不是楔子数？
/// </summary>
/// <param name="x"></param>
/// <returns></returns>
public bool IsSphenic(int x)
{
	return sphenicHash.ContainsKey(x);
}

/// <summary>
/// 返回计算公式
/// </summary>
/// <param name="x"></param>
/// <returns></returns>
public string SphenicExpression(int x)
{
	if (sphenicHash.ContainsKey(x))
	{
		return sphenicExpressions[(int)sphenicHash[x]];
	}
	return "";
}