快速排序(快排) (C语言实现)

🔆欢迎来到我的【数据结构】专栏🔆

• 👋我是Brant_zero，一名学习C/C++的在读大学生。
• 🌏?我的博客主页????????Brant_zero的主页
• 🙏🙏欢迎大家的关注，你们的关注是我创作的最大动力🙏🙏

🍁前言

????????本篇博客学习内容是快速排序，快速排序有多种不同的版本和优化，我们这次的目的就是将这些版本都搞明白，废话不多说，我们开始。

? ? ? ? 篇幅较长，建议配合目录来浏览。

🍂目录🍂

一、快排介绍与思想

二、hoare版本

2.1 单趟过程

2.2 多趟过程

2.3 多趟的实现

三、 挖坑法

四、 前后指针法

五、 快排的优化

5.1 三数取中选key

5.2 小区间改造

六、 快速排序改非递归版本

---

一、快排介绍与思想

快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法。

💡单趟过程：

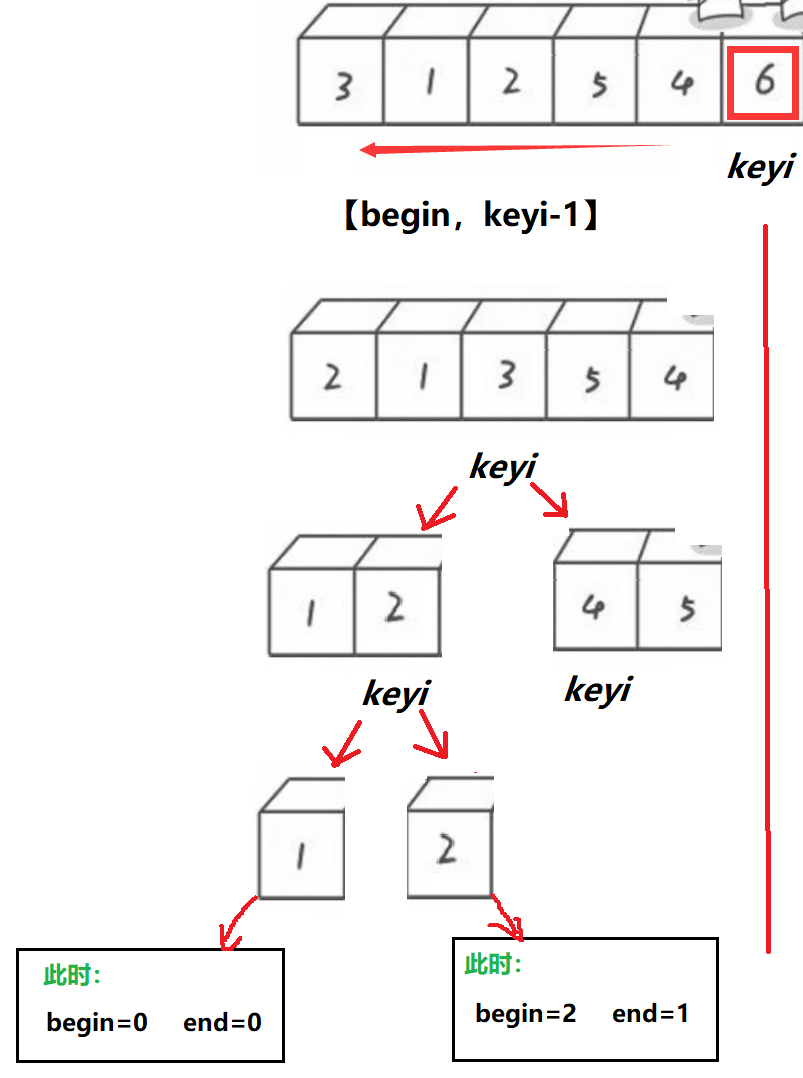
1. ?首先记录下keyi位置，然后left和right分别从数组两端开始往中间走。
2. right先开始向中间行动，如果right处的值小于keyi处的值，则停止等待left走。
3. left开始行动，当left找到可以keyi处小的值时，left和right处的值进行交换。
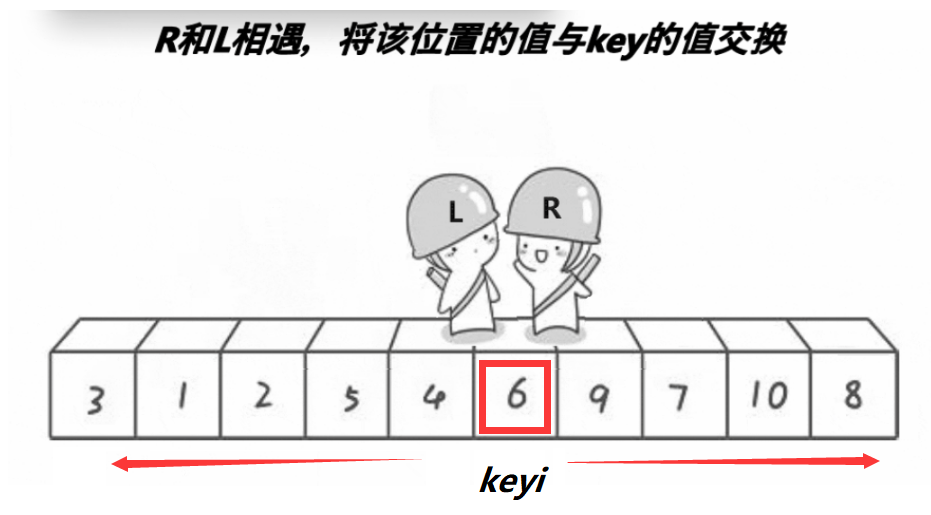
4. 当两个位置相遇时，将相遇位置的值与keyi处的值进行交换，并将相遇的位置置为新的keyi。

我们来看看下面的代码，然后来分析其中容易出现的错误。

    //单趟：
	//首先keyi记录begin处的数据
	int keyi = begin;
	int left = begin;
	int right = end;
	//两个指针开始往中间行动
	while (left < right)
	{
		//right先行动，一定要找到 大于 keyi位置的值
		while(left < right && a[right] >= a[keyi])
		{
			right--;
		}
		//left行动，一定要找到 小于 keyi位置的值
		while (left < right && a[left] <= a[keyi])
		{
			left++;
		}
		//到达指定位置，进行交换
		swap(&a[left], &a[right]);
	}
	//走完上面的步骤后，两个下标会相聚在一个位置
	//然后对这两个位置的值进行交换
	swap(&a[right], &a[keyi]);
	keyi = right;
	//[begin,keyi-1],keyi,[keyi+1],end

💡易错点：

1. 如果keyi记录的最左边的数据，则要让right指针先行动，因为这样一定能要保证相遇的地方比keyi处的值要小。相遇位置就是R停下来的位置，好的情况是right处的值比keiy处的小，最坏的情况就是right走到了keyi的位置，那此时交换也坏没有影响。
2. 找值时，left或right处的值一定要比keyi处的小(大)，等于也不行，如果出现以下这种情况会死循环。
3. 在left和right往中间找值时要判断left<right，如果不控制，left或right很容易走出数组。

2.2 多趟过程

当上面的单趟走完后，我们会发现，keyi左边的全是小于a[keyi]的，右边全是大于a[keyi]的。

那我们一直重复这个单趟的排序，就可以实现对整个数组的排序了，这典型是一个递归分治的思想。

💡基本思路：

1. 将keyi分为两边，分别进行递归，类似二叉树的前序遍历。
2. 划分为[begin,keyi-1],? keyi,? ?[keyi+1,end].
3. 递归结束条件：当begin == end? 或者是 数组错误(begin>end)时，则为结束条件。

2.3 多趟的实现

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	//一趟的实现
	int left = begin;
	int right = end;
	int keyi = left;
	while (left < right)
	{
		//右边开始行动   一定要加上等于，因为快速排序找的是一定比它小的值
		while (left < right && a[keyi] <= a[right])
		{
			right--;
		}
		//左边开始行动
		while (left < right &&   a[left] <= a[keyi])
		{
			left++;
		}
		swap(&a[left], &a[right]);

	}
	swap(&(a[keyi]), &(a[right]));
	keyi = right;
	//[begin,keyi-1] keyi [keyi+1,end]
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi+1, end);
}

效果检验：

---

三、 挖坑法

想必仍有人对hoare版本中，为什么左边置为keyi右边就要先走无法理解，这里有人就想出了一种新的快排版本，虽然算法思路一样，但是更有利于理解。

其次，这两种办法单趟走出来的结果不同，这就导致一些题目上对于快排单趟的结果不同，所以我们来理解一下这种挖坑法的算法思想。

我们先来看看下面的动画：

💡算法思路：

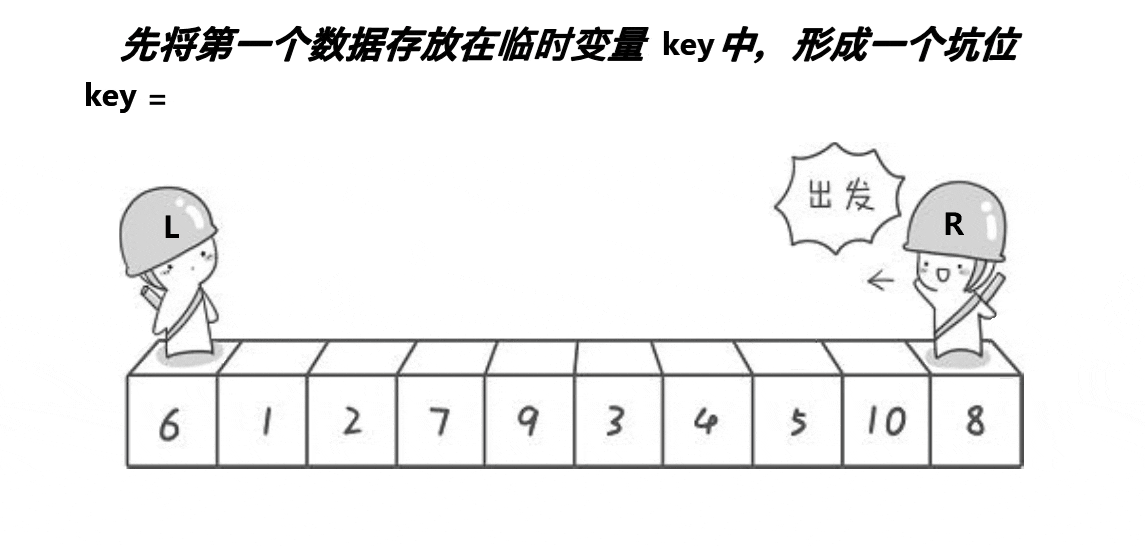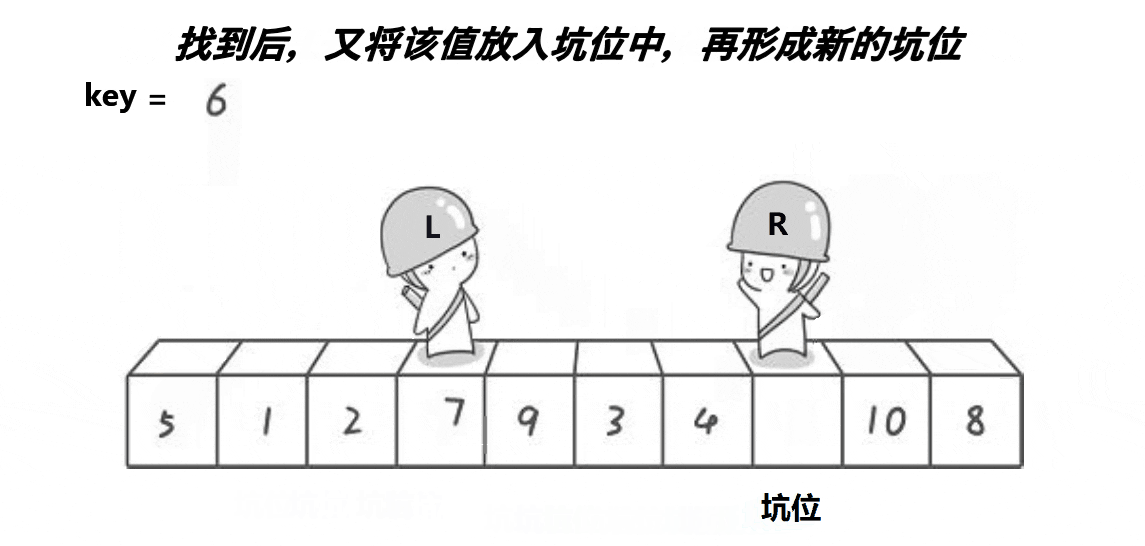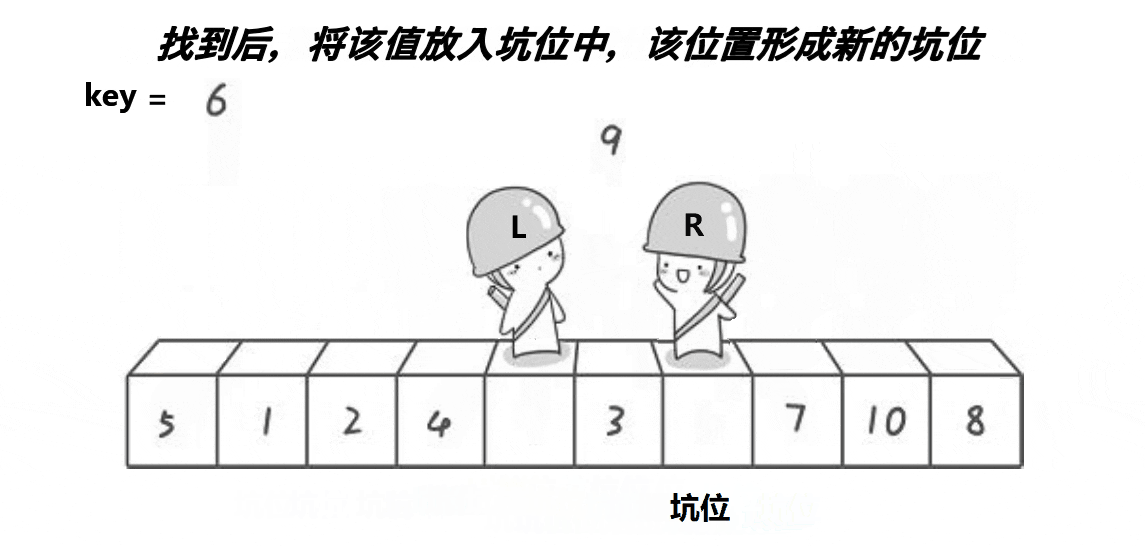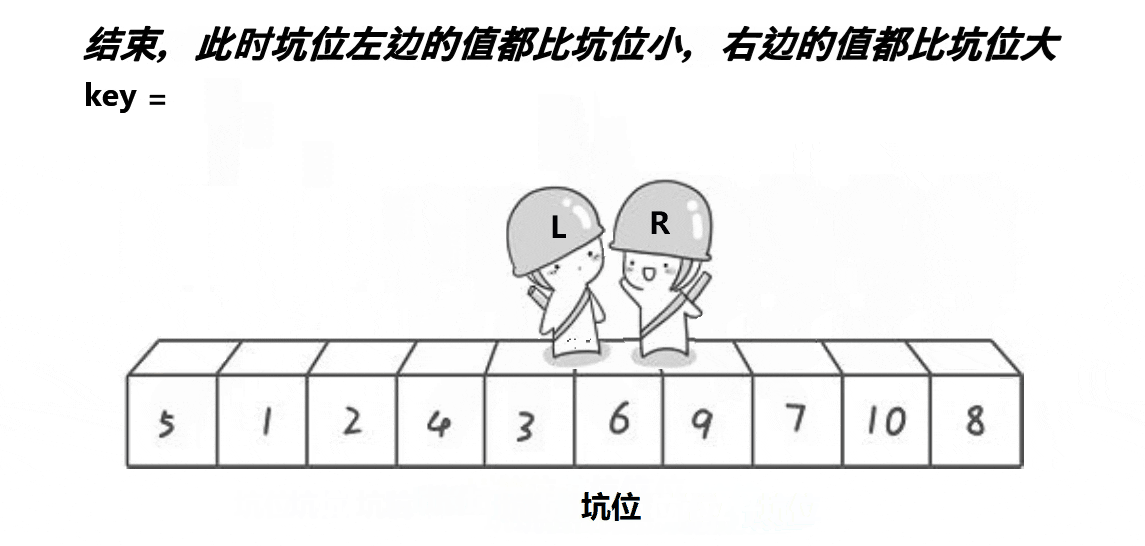
1. 将begin处的值放到key中，将其置为坑位(pit)，然后right开始行动找值补坑。
2. right找到比key小的值后将值放入坑位，然后将此处置为新的坑。
3. left也行动开始找值补坑，找到比key大的值将其放入坑位，置为新的坑。
4. 当left与right相遇的时候，将key放入到坑位中。
5. 然后进行[begin,piti-1],? piti,? ?[piti+1,end] 的递归分治。

因为有了hoare版本的实现，所以这里就不多赘述了，上面的算法思路已经将过程表述的很清楚了。

//快排  挖坑法
void QuickSort_dig(int* a, int begin, int end)
{
	if (begin >= end)
		return;
	//一趟的实现
	int key = a[begin];
	int piti = begin;
	int left = begin;
	int right = end;
		while (left < right)
		{
			while (left < right && a[right] >= key)
			{
				right--;
			}
			a[piti] = a[right];
			piti = right;
			while (left < right && a[left] <= key)
			{
				left++;
			}
			a[piti] = a[left];
			piti = left;
		}
		//补坑
		a[piti] = key;
	//[begin, piti - 1] piti [piti + 1, end]
	QuickSort_dig(a, begin, piti - 1);
	QuickSort_dig(a, piti + 1, end);
}

?效果检验：

---

四、 前后指针法

前后指针法相比于hoare和挖坑法，不论是算法思路还是实现过程都有很大提升，也是主流的一种写法，这里我们一样来看看单趟的过程吧。

💡算法思路：

1. cur位于begin+1的位置，prev位于begin位置，keyi先存放begin处的值。
2. cur不断往前+1,直到cur >= end时停止循环。
3. 如果cur处的值小于key处的值，并且prev+1 != cur，则与prev处的值进行交换。
4. 当循环结束时，将prev处的值与keyi的值相交换，并将其置为新的keyi位置。

代码实现：

void QuickSort_Pointer(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	//数据区间大与10，进行快速排序
    int prev = begin;
	int cur = begin + 1;
	int keyi = begin;
	//三数取中后对keyi位置的值进行交换
	int mid = GetMid(a, begin, end);
	swap(&a[mid], &a[keyi]);
	while (cur <= end)
	{
		//cur一直往前走，如果碰到小于并且prev++不等于cur则交换，
		//因为如果prev+1 == cur 则会发生自己与自己交换的情况
		if (a[cur] < a[keyi] && ((++prev) != cur))
		{
			swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	swap(&a[prev], &a[keyi]);
	keyi = prev;
	//开始进行递归
	QuickSort_Pointer(a, begin, keyi - 1);
	QuickSort_Pointer(a, keyi + 1, end);
}

注意点：

1. 在遍历的过程中，cur是不断向前的，只是cur处的值小于keyi处的值时，才需要进行交换判断一下。
2. 在cur位置处的值小于keyi处的值时，要进行判断prev++是否等于cur，如果等于，那么会出现自己与自己交换的情况。如果相等，则不进行交换。

五、 快排的优化

5.1 三数取中选key

在实现了快速排序之后，我们发现，keyi的位置，是影响快速排序效率的重大因素。因此有人采用了三数取中的方法解决选keyi不合适的问题。

三数取中

即知道这组无序数列的首和尾后，我们只需要在首，中，尾这三个数据中，选择一个排在中间的数据作为基准值(keyi)，进行快速排序，即可进一步提高快速排序的效率。

//三数取中
int GetMid(int *a,int begin, int end)
{
	int mid = (begin + end) / 2;
	if (a[begin] > a[end])
	{
		if (a[end] > a[mid])
			return end;
		else if (a[mid] > a[begin])
			return begin;
		else
			return mid;
	}
	else
	{
		if (a[end] < a[mid])
			return end;
		else if (a[end] < a[begin])
			return begin;
		else
			return mid;
	}
}

?这样，中间值的下标就被返回过来了，然后我们将这个位置换为新的keyi，就可以了。

5.2 小区间改造

由于快速排序是递归进行的，当递归到最后几层时，此时数组中的值其实已经接近有序，而且这段区间再递归会极大占用栈(函数栈帧开辟的地方)的空间,

接下来，我们对其进行优化，如果区间数据量小于10，我们就不进行递归快速排序了，转而使用插入排序。

我们来看看使用了小区间改造优化和三数取中优化后的快排。

void QuickSort_Pointer(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	//数据区间大与10，进行快速排序
	if (end - begin > 10)
	{
		int prev = begin;
		int cur = begin + 1;
		int keyi = begin;
		//三数取中后对keyi位置的值进行交换
		int mid = GetMid(a, begin, end);
		swap(&a[mid], &a[keyi]);
		while (cur <= end)
		{
			if (a[cur] < a[keyi] && ((++prev) != cur))
			{
				swap(&a[cur], &a[prev]);
			}
			cur++;
		}
		swap(&a[prev], &a[keyi]);
		keyi = prev;
		//开始进行递归
		QuickSort_Pointer(a, begin, keyi - 1);
		QuickSort_Pointer(a, keyi + 1, end);
	}
	else
	{
		//左闭右闭
		InsertSort(a, end - begin + 1);
		InsertSort(a + begin, end - begin + 1);
	}

}

💡注意点：

1. 插入排序之后两个参数，一个是数据集合的起点地址，第二个是数据量。
2. 使用插入排序时，我们要传入待排序数据集合的其实地址，即a+begin，如果传入的是a，那排序的永远都是数组a的前n个区间。
3. 插入排序传入的是数据个数，所以我们要将end-begin加上1之后才传入。快速排序中end、begin都是闭区间(即数组下标)。

六、 快速排序改非递归版本

因为函数栈帧是在栈(非数据结构上的栈)上开辟的，所以容易出现栈溢出的情况，为了解决这个问题，我们除了上面两种优化，还可以将快速排序改为非递归版本，这样空间的开辟就在堆上了，堆上的空间比栈要多上许多。

为了实现快速排序的非递归版本，我们要借助我们以前实现的栈，来模拟非递归。

💡实现思路：

1. 入栈一定要保证先入左再入右。
2. 取两次栈顶的元素，然后进行单趟排序。
3. 划分为[left , keyi - 1] keyi [ keyi +? 1 , right ] 进行右、左入栈。
4. 循环2、3步骤直到栈为空。

int PartSort(int * a, int begin, int end)
{
	int prev = begin;
	int cur = begin + 1;
	int keyi = begin;
	int mid = GetMid(a, begin, end);
	swap(&a[mid], &a[keyi]);
	while (cur <= end)
	{
		if (a[cur] < a[keyi] && ((++prev) != cur))
		{
			swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	swap(&a[prev], &a[keyi]);
	return prev;
}
void QuickSortNonR(int* a, int begin, int end)
{
	ST st;
	StackInit(&st);
	//先入右 再入左
	StackPush(&st, end);
	StackPush(&st, begin);
	while (!StackEmpty(&st))
	{
		//那出栈 则是先出左再出右
		int left = StackTop(&st);
		StackPop(&st);
		int right = StackTop(&st);
		StackPop(&st);
		int keyi = PartSort(a, left, right);
		//[left, keyi - 1] keyi[keyi + 1, right];
		//栈里面的区间  都会进行单趟排序分割

		if (keyi + 1 < right)//说明至少还有两个数据
		{
			//入右然后入左
			//才能保证取出时 顺序不变
			StackPush(&st, right);
			StackPush(&st, keyi + 1);
		}
		//如果小于，说明至少还有两个元素 待排序
		if (left < keyi - 1)
		{
			//入右然后入左
			StackPush(&st, keyi - 1);
			StackPush(&st, left);
		}
	}
	StackDestory(&st);
}

效果演示：

---

总结

本篇介绍了hoare法、挖坑法、前后指针法，以及两种快排的优化方式和非递归版本，还是非常有难度的，检验大家实现的时候多看看动图，然后自己尝试写一下单趟的过程，再结合博客的内容理解快排递归的思路。这篇的内容相对硬核，光看是很难理解的，尤其是接触hoare版本和非递归版本，希望大家动手配合调试、画图来实现。

好的，本篇博客到此就结束了，下篇博客会更新归并排序的相关内容，希望大家持续关注，可以的话点个免费的赞或者关注一下啊，你们反馈是我更新最大的动力。