力扣第一题-两数之和[简单]

题目描述

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

提示：

• 2 <= nums.length <= 10^4
• -10^9 <= nums[i] <= 10^9
• -10^9 <= target <= 10^9
• 只会存在一个有效答案

进阶：你可以想出一个时间复杂度小于 O(n2) 的算法吗？

解法

暴力枚举

public int[] twoSum(int[] nums, int target) {
    int n = nums.length;
    for (int i = 0; i < n; ++i) {
        for (int j = i + 1; j < n; ++j) {
            if (nums[i] + nums[j] == target) {
                return new int[]{i, j};
            }
        }
    }
    return new int[]{};
}

明显这个算法的时间复杂度是 O(N2)，题目里问我 你可以想出一个时间复杂度小于 O(n2) 的算法吗？ 那我就得想一想了。。

二分查找（失败了）

二分查找只适用于有序数组

public int[] twoSum(int[] nums, int target) {
    // 先进行升序排序
    sort(nums);
    int length = nums.length;
    for (int i = 0; i < length; i++) {
        int findNum = target - nums[i];

        int leftIndex = i + 1;
        int rightIndex = length - 1;
        int index = binarySearch(nums, findNum, leftIndex, rightIndex);
        if (index != -1) {
            // 找到目标值，返回索引数组
            return new int[]{i, index};
        }
    }
    return new int[]{};
}

/**
 * 二分查找
 *
 * @param nums 数组
 * @param findNum 要查找的数值
 * @param left 左边索引
 * @param right 右边索引
 * @return 查询到的索引，未查询到返回-1
 */
private int binarySearch(int[] nums, int findNum, int left, int right) {
    while (left <= right) {
        int mid = left + (right - left) / 2;

        if (nums[mid] == findNum) {
            // 找到目标值，返回索引
            return mid;
        } else if (nums[mid] > findNum) {
            // 目标值在左半部分，更新右边界
            right = mid -1;
        } else {
            // 目标值在右半部分，更新左边界
            left = mid + 1;
        }
    }
    return -1;
}

输入数组 [3, 2, 4]， 查找相加结果等于6 的两个数的索引

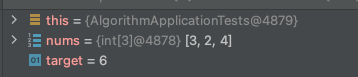
上述代码返回的结果是 [0,2] 3+4显然是不等于6的

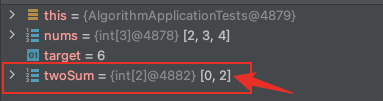
原因是在代码开始执行 sort 后，数组的顺序发生了变化，虽然可以找到 相加等于target的两个数值，但无法找到最初对应的索引。除非，被查找的数组是个有序数组

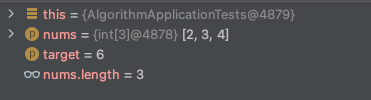
因此，二分查找只对有序数组有效！！

哈希表

用哈希表实现就很简单了，准备一个map，以数值做为key，以索引作为value

遍历数组，查询map中是否存在目标值，存在返回 当前索引 以及 map中存储的目标值对应的索引；不存在 则向map中插入当前数值及索引

时间复杂度和空间复杂度都是O(N)

public int[] twoSum(int[] nums, int target) {
    HashMap<Integer, Integer> numsMap = new HashMap<>();
    for (int i = 0; i < nums.length; i++) {
        int targetNum = target - nums[i];
        if (numsMap.containsKey(targetNum)) {
            return new int[]{i, numsMap.get(targetNum)};
        }
        numsMap.put(nums[i], i);
    }
    return new int[]{};
}