初赛冲刺模拟赛一————答题中

1.【 单选 】2 分

2023年全国青少年信息学奥林匹克竞赛（NOI）在(? )举办

• A.

  北京

• B.

  长沙

• C.

  广州

• D.

  成都

A

B

C

D

2.【 单选 】2 分

计算机开机后，操作系统最终被加载到(? )中。

• A.

  硬盘

• B.

  CPU

• C.

  内存

• D.

  显示器

A

B

C

D

3.【 单选 】2 分

使用链式存储具有n个节点的二叉树中，指为NULL的指针的个数为(? )。

• A.

  n-1

• B.

  n+1

• C.

  2n-1

• D.

  2n+1

A

B

C

D

4.【 单选 】2 分

关于链式存储结构，下列说法错误的是(? )。

• A.

  比顺序存储结构查找节点速度快

• B.

  比顺序存储结构存储密度小

• C.

  每个节点都是由指针域和数据域组成

• D.

  逻辑上不相邻的节点物理上可能相邻

A

B

C

D

5.【 单选 】2 分

Base64编码是一种基于64个可打印字符来表示二进制数据的编码方法，Base64 编码要求把3个8位的字节（3*8=24）转化为4个6位（4*6=24），之后在每个6位的前面补两个0，形成8位一个字节的形式。如果剩下的字符不足3个字节，则用0填充至3个字节。若将字符串“abcd”使用Base64进行编码，则编码后占用的空间为(? )字节。

• A.

  4字节

• B.

  6字节

• C.

  8字节

• D.

  12字节

A

B

C

D

6.【 单选 】2 分

共5个元素，往入栈顺序为ABCDE，则出栈顺序不可能是(? )。

• A.

  BACDE

• B.

  ACDBE

• C.

  AEBCD

• D.

  AEDCB

A

B

C

D

7.【 单选 】2 分

在C++语言中，下列与定义语句 int *p[3]等价的是(? )。

• A.

  int *(p[3])

• B.

  int (*p)[3]

• C.

  int p[3]*

• D.

  int **p

A

B

C

D

8.【 单选 】2 分

若数组arr={2, 12, 20, 31, 56, 80}，使用折半查找算法查找56，需要执行(? )次才能查找成功。

• A.

  1

• B.

  2

• C.

  3

• D.

  4

A

B

C

D

9.【 单选 】2 分

已知二叉树的中序遍历是：a*b+d*c-f/e，后序遍历是：ab*d+cfe/-*，则其前序遍历为(? )。

• A.

  **a+bd-c/fe

• B.

  *+*abd-ce/f

• C.

  +*ab-*dc/fe

• D.

  *+*abd-c/fe

A

B

C

D

10.【 单选 】2 分

十六进制的10.4相当于 (? )。

• A.

  二进制的10000.1

• B.

  六进制的24.13

• C.

  八进制的20.25

• D.

  十进制的16.5

A

B

C

D

11.【 单选 】2 分

一个具有1025个结点的二叉树的高度为(? )。

• A.

  10

• B.

  11

• C.

  10～1024

• D.

  11～1025

A

B

C

D

12.【 单选 】2 分

若对如下无向图进行遍历，则下列选项中，不是广度优先遍历序列的是(? )。

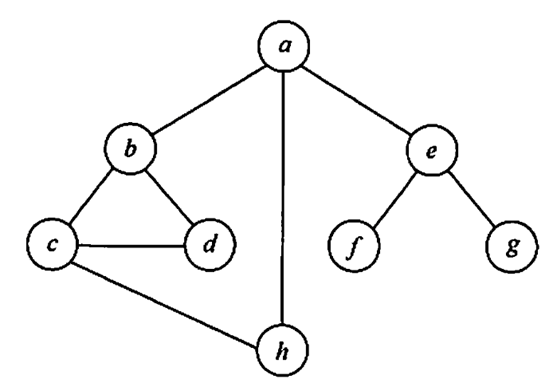
• A.

  h,c,a,b,d,e,g,f

• B.

  e,a,f,g,b,h,c,d

• C.

  d,b,c,a,h,e,f,g

• D.

  a,b,c,d,h,e,f,g

A

B

C

D

13.【 单选 】2 分

这次比赛一共有8个相同的奖品，分到6个班级，每个班级至少一个，一共有(? )种分法。

• A.

  15

• B.

  21

• C.

  28

• D.

  56

A

B

C

D

14.【 单选 】2 分

某比赛共有5名选手A、B、C、D、E，三条道路，其中AB两名选手必须走同一条路，每条路必须有至少一名选手，现要为选手分配道路，一共有(? )种分法。

• A.

  36

• B.

  6

• C.

  72

• D.

  60

A

B

C

D

15.【 单选 】2 分

执行完下列语句段之后，i的值为(? )。

int f(int x) {
    return ( (x>0) ? x*f(x-1) : 2)
}
int i=f(f(2));
i = f(f(2));

• A.

  8

• B.

  48

• C.

  36

• D.

  无限递归

A

B

C

D

16.【 单选 】1.5 分

二、阅读程序(程序输入不超过数组或字符串定义的范围；?判断题正确填√，错误填×；除特

殊说明外，判断题?1.5?分，选择题?3?分，共计?40?分)

（一）

01 #include<iostream>
02 #include<stack>
03 #include<vector>
04 using namespace std;
05 
06 int a[2000];
07 stack<int> sta;
08 int main(){
09     int n;
10     cin >> n;
11     for(int i = 0; i < n; i ++) {
12         cin >> a[i];
13     }
14     vector<int> ans(n, -1);
15     for(int i = n-1; i >= 0; -- i){
16         while(!sta.empty() && a[sta.top()]<=a[i])
17             sta.pop();
18         if(!sta.empty())
19             ans[i] = sta.top();
20         sta.push(i);
21     }
22     for(int i = 0; i < n; ++ i){
23         printf("%d ", ans[i] + 1);
24     }
25     return 0;
26 } 

完成下面的判断题和单选题：

判断题

若输入的n为2001，程序不会发生错误。( ?)

• A.

  正确

• B.

  错误

A

B

17.【 单选 】1.5 分

第14行的含义是声明一个长度为n的vector容器，并将其元素初始化为-1。(? )

• A.

  正确

• B.

  错误

A

B

18.【 单选 】1.5 分

第15行“-- i”改成“i --”，答案不变。 (? )

• A.

  正确

• B.

  错误

A

B

19.【 单选 】1.5 分

第16行“!sta.empty() && a[sta.top()]<=a[i]”改成a[sta.top()]<=a[i] && !sta.empty()”，程序不会发生错误。 (? )

• A.

  正确

• B.

  错误

A

B

20.【 单选 】3 分

若输入为“2 1 1”，输出为(? )。

• A.

  1 1

• B.

  0 0

• C.

  1

• D.

  0

A

B

C

D

21.【 单选 】3 分

若输入为“5 1 2 3 4 5”，则输出为 (? )。

• A.

  1 2 3 4 5

• B.

  2 3 4 5 1

• C.

  5 4 3 2 1

• D.

  2 3 4 5 0

A

B

C

D

22.【 单选 】1.5 分

（二）

01 #include<iostream>
02 using namespace std;
03
04 int main()
05 {
06     int n, count = 0;
07     cin >> n;
08     for(int i = 0; i <= n/5; i++) {
09         for(int j = 0; j <= n/2; j++) {
10             if((i*5 + j*2) > n) {
11                 break;
12             }
13             else {
14                 count++;
15             }
16         }
17     }
18     cout << count << endl;
19     return 0;
20 }

完成下面的判断题和单选题：

判断题?

若将第8行“i <= n/5”改成“i <= n”，答案不变。( ?)

• A.

  正确

• B.

  错误

A

B

23.【 单选 】1.5 分

若将第9行“i <= n/2”改成“i <= n”，答案不变。(? )

• A.

  正确

• B.

  错误

A

B

24.【 单选 】1.5 分

若将第11行“break;”删掉，不影响计算答案。 (? )

• A.

  正确

• B.

  错误

A

B

25.【 单选 】3 分

该算法的时间复杂度为(? )。

• A.

  0(n)

• B.

  0(n+n)

• C.

  0(n^2)

• D.

  0(nlogn)

A

B

C

D

26.【 单选 】3 分

若输入为10，第11的“break”语句执行(? )次。

• A.

  1

• B.

  2

• C.

  3

• D.

  4

A

B

C

D

27.【 单选 】3 分

若输入为9，则输出为 (? )。

• A.

  6

• B.

  7

• C.

  8

• D.

  9

A

B

C

D

28.【 单选 】1.5 分

（三）

01 #include<iostream>
02 #include<vector>
03 
04 using namespace std;
05 
06 int len, n, ans, cnt;
07 vector<int> num;
08 
09 void solve(int x)
10 {
11     while(x)
12     {
13         num.push_back(x%10);
14         x /= 10;
15     }
16     reverse(num.begin(), num.end());
17     len = num.size();
18     return ;
19 }
20 
21 int count(int a, int b)
22 {
23     cnt = 0; 

24     int fr = 0, mid = num[b], be = 0;
25     for(int i = 0; i < b; i++)
26         fr = fr*10+num[i];
27     for(int i = b+1; i < len; i++)
28         be = be*10+num[i];
29     if(!a && !fr) return 0;
30 
31     if(a)
32         cnt += fr*pow(10, len-b-1);
33     else
34         cnt += (fr-1)*pow(10, len-b-1);
35     if(a == mid) cnt += be+1;
36     else if(mid > a) cnt += pow(10, len-b-1);
37 
38     return cnt;
39 }
40 
41 int main()
42 {
43     while(cin >> n)
44     {
45         num.clear();
46         solve(n);
47         for(int i = 0; i <= 9; i++)
48         {
49             ans = 0;
50             for(int j = 0; j < len; j++)
51                 ans += count(i, j);
52             if(ans != 0)
53                 cout << i << " " << ans << endl;
54         }
55     }
56     return 0;
57 }

假设输入的?n?在int?范围内，完成下面的判断题和单选题：

? 判断题

第45行代码删掉，不会影响答案。(? )

• A.

  正确

• B.

  错误

A

B

29.【 单选 】1.5 分

num数组可能会发生越界风险。(? )

• A.

  正确

• B.

  错误

A

B

30.【 单选 】1.5 分

若输入为0，则程序不会输出也不会结束。(? )

• A.

  正确

• B.

  错误

A

B

31.【 单选 】3 分

当输入为3时，输出为(? )。

• A.

  1 1

  2 1

  3 1

• B.

  1 0

  2 0

  3 0

• C.

  1 1

• D.

  3 1

A

B

C

D

32.【 单选 】3 分

当输入为54321时，第14行语句执行(? )次。

• A.

  2?

• B.

  3?

• C.

  4

• D.

  5

A

B

C

D

33.【 单选 】4 分

（4分）当输入为“10时，输出为(? )。

• A.

  0 1

  1 1

  2 1

  3 1

  4 1

  5 1

  6 1

  7 1

  8 1

  9 1

• B.

  0 1

  1 2

  2 1

  3 1

  4 1

  5 1

  6 1

  7 1

  8 1

  9 1

• C.

  0 1

  1 1

• D.

  1 1

  0 1

A

B

C

D

34.【 单选 】3 分

三、?? 完善程序(单选题，每小题?3?分， 共计?30?分)

(1)?(区间合并) 给定n个区间，每个区间用[l,r]表示，要求合并所有重叠区间，并输出合并后的区间。如区间合并前为：[1,3][2,6][8,10][15,18]，合并后为[1,6][8,10][15,18]

试补全程序。

01 #include<iostream>
02 using namespace std;
03 
04 struct node {
05     int x, y;
06 }a[100005];
07 int b[100005][2];
08 
09 bool cmp(node o1, node o2) {
10     return ①;
11 }
12 
13 int main() {
14 
15     int n;
16     cin >> n;
17     for(int i = 0; i < n; i ++) {
18         cin >> a[i].x >> a[i].y;
19     }
20     sort(a, a + n, cmp); 

21     ②;
22     for(int i = 0; i < n; i ++) {
23         int l = a[i].x, r = a[i].y;
24         if(k == 0 || ③) {
25             b[k][0] = l;
26             ④;
27         } else {
28             b[k-1][1] = ⑤;
29         }
30     }
31     for(int i = 0; i < k; i ++) {
32         cout << b[i][0] << " " << b[i][1] << endl;
33     }
34     return 0;
35 }

①处应填(? )

• A.

  o1.x >?o2.x

• B.

  o1.x <?o2.x?

• C.

  o1.y >?o2.y

• D.

  o1.y <?o2.y

A

B

C

D

35.【 单选 】3 分

?②处应填(? )

• A.

  int k = 0

• B.

  int k = 1

• C.

  int k = -1

• D.

  int k = 2

A

B

C

D

36.【 单选 】3 分

③处应填(? )

• A.

  b[k-1][1] < r

• B.

  b[k-1][1] <= r

• C.

  b[k-1][1] < l

• D.

  b[k-1][1] <= l

A

B

C

D

37.【 单选 】3 分

④处应填(? )

• A.

  b[k][1] = l

• B.

  b[++k][1] = r

• C.

  b[k][1] = r

• D.

  b[k++][1] = r

A

B

C

D

38.【 单选 】3 分

⑤处应填(? )

• A.

  max(b[k-1][1], r)

• B.

  max(b[k][1], r)

• C.

  max(b[k-1][0], l)

• D.

  max(b[k][0], l)

A

B

C

D

39.【 单选 】3 分

(2)?(最接近的三数之和) 输入一个长度为n（1<=n<=1000）的整数数组nums(-1000<=nums[i]<=1000)和一个目标值target(-10000<=target<=10000)，要求从nums里选出三个整数，使它们的和与target接近，输出三个整数的和。保证只存在一组解。

试补全程序。

01 #include<iostream>
02 
03 using namespace std;
04 const int N = 1005;
05 int nums[N];
06 int n, target;
07 
08 int main() {
09     cin >> n >> target;
10     for(int i = 0; i < n; i ++) {
11         cin >> nums[i];
12     }
13     int res = 0;
14     int mn = INT32_MAX;
15     ①;
16     for (int i = 0; i < n; i++) {
17         int l =②, r = n - 1;
18         while (l < r) {
19             int cur = nums[i] + nums[l] + nums[r];
20             int t = ③;
21             if (t < mn) {
22                 mn = t;
23                 res = cur;
24             }
25             if (cur == target)
26                 ④;
27             else if (cur < target)
28                 ⑤;
29             else
30                 r--;
31         }
32			  if(res == target) break;
33     }
34     cout << res << endl;
35     return 0;
36 } 

①处应填(? )

• A.

  sort(nums, nums + n)

• B.

  sort(nums + 1, nums + n)

• C.

  sort(nums, nums + n + 1)

• D.

  sort(nums + 1, nums + n + 1)

A

B

C

D

40.【 单选 】3 分

②处应填(? )

• A.

  0

• B.

  i - 1

• C.

  i

• D.

  i + 1

A

B

C

D

41.【 单选 】3 分

③处应填(? )

• A.

  cur

• B.

  target

• C.

  abs(cur – target)

• D.

  abs(target - cur)

A

B

C

D

42.【 单选 】3 分

④处应填(? )

• A.

  continue

• B.

  break

• C.

  return 0

• D.

  exit

A

B

C

D

43.【 单选 】3 分

⑤处应填(? )

• A.

  l --

• B.

  l ++

• C.

  r --

• D.

  r ++

A

B

C

D