【机器学习】决策树
发布时间:2023年12月23日
参考课程视频:https://www.icourse163.org/course/NEU-1462101162?tid=1471214452
1 概述
样子:
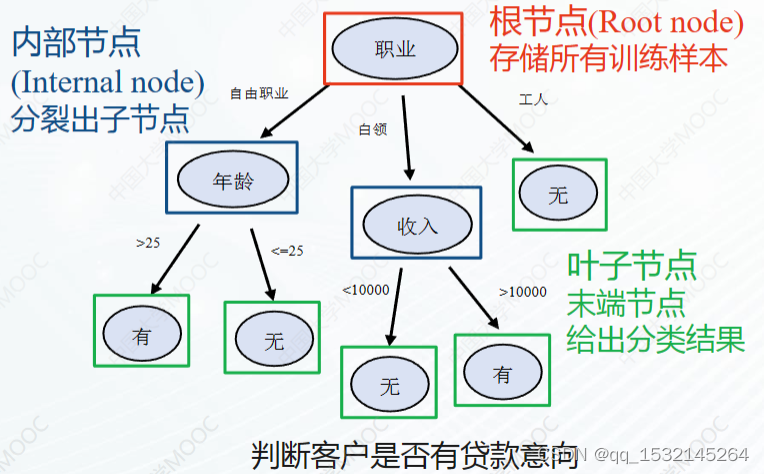
2 分裂
2.1 分裂原则
信息增益


信息增益比

基尼指数

3 终止 & 剪枝
3.1 终止条件
- 无需分裂
- 当前节点内样本同属一类
- 无法分裂
- 当前节点内所有样本的特征向量完全相同
- 采用任何特征都无法将当前样本集分为多个子类
- 无数据可分
- 当前节点内没有样本
3.2 剪枝
剪枝的目的:解决决策树过拟合现象(决策树规模大),提高决策树的泛化性能。
剪枝方法
- 前剪枝(预剪枝)
- 在决策树的生成过程中同步进行剪枝
- 在节点进行分裂前,对比节点分裂前后决策树的泛化性能指标,若泛化性能在分裂后得到提升,执行分裂;否则不执行分裂。
- 后剪枝
- 在决策树完全生成后逐步剪去叶子节点
- 常采用启发式方法从最深层的叶子节点或具有最高不纯度的
叶子节点开始剪枝 - 通过对比剪枝前后的泛化指标,决定是否剪去该叶子节点。
前剪枝 & 后剪枝 策略对比:
| 策略 | 时间 | 拟合风险 | 泛化能力 |
|---|---|---|---|
| 前剪枝 | 训练时间较少、测试时间较少 | 过拟合风险较低 、欠拟合风险较高 | 泛化能力一般 |
| 后剪枝 | 训练时间较长、测试时间较少 | 过拟合风险较低、欠拟合风险稳定 | 泛化能力较好 |
通常后剪枝比前剪枝保留的决策树规模更大。
4 决策树算法
4.1 经典决策树算法
ID3

C4.5

CART(Classification And Regression Tree)

4.2 算法对比分析
| 算法 | 特征选择 | 剪枝 | 处理数据类型 | 树类型 |
|---|---|---|---|---|
| ID3 | 信息增益 | 无 | 离散 | 多叉树 |
| C4.5 | 信息增益比 | 前剪枝 | 离散、连续 | 多叉树 |
| CART | 基尼指数 | 后剪枝 | 离散、连续 | 二叉树 |
总结:
- CART的功能更全:分类、回归
- CART具有更好的泛化性能:二叉树,后剪枝。
- CART训练时间较长,计算开销较大。
- 信息增益、信息增益比和基尼指数各有利弊。
文章来源:https://blog.csdn.net/qq_1532145264/article/details/135149213
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 华为OD机试真题-可以组成网络的服务器-2023年OD统一考试(C卷)
- R语言【utils】——write.table(),write.csv(),write.csv2():将数据写入文件
- vue $set 报错 Cannot use ‘in‘ operator to search for ‘imgs‘ in
- OSCHINA & Gitee 联合呈现,《2023 中国开源开发者报告》正式发布,总结分非常帮,可以免费看的报告!
- [Java][线程][线程的基础认知]创建/使用/定时
- 【每日一题】2707. 字符串中的额外字符-2024.1.9
- DS18B20温度传感器(STM32F103C8T6)串口发送到电脑
- rpc和http的区别,使?场景
- 【教学类-42-03】20231225 X-Y 之间加法题判断题3.0(确保错误题有绝对错误的答案)
- 《Python数据分析技术栈》第05章 04 切片或选择数据子集(Slicing or selecting a subset of data)