运筹说 第65期 | 动态规划的基本概念和基本原理

20世纪50年代初，美国数学家R. Bellman 等人在解决多阶段决策优化问题时提出了一种高效的求解方法——动态规划（Dynamic Programming），该方法基于多阶段决策优化问题的特点，把多阶段问题转换为一系列互相联系的单阶段问题，然后逐一解决。

相比于线性规划方法，动态规划由于其独特的解题思路，在路径优化、资源分配、生产调度、库存管理和投资组合等优化问题上更加高效，并成功解决了交通运输、生产管理、工程技术、军事决策等领域的许多实际问题。

动态规划模型可以分为离散确定型、离散随机型、连续确定型和连续随机型四种，其中，离散确定型是最基本的一种类型。

因此，本期开始，小编将主要针对离散确定型问题，从基本概念、基本原理、模型建立和求解方法以及具体应用等方面对动态规划问题进行介绍。

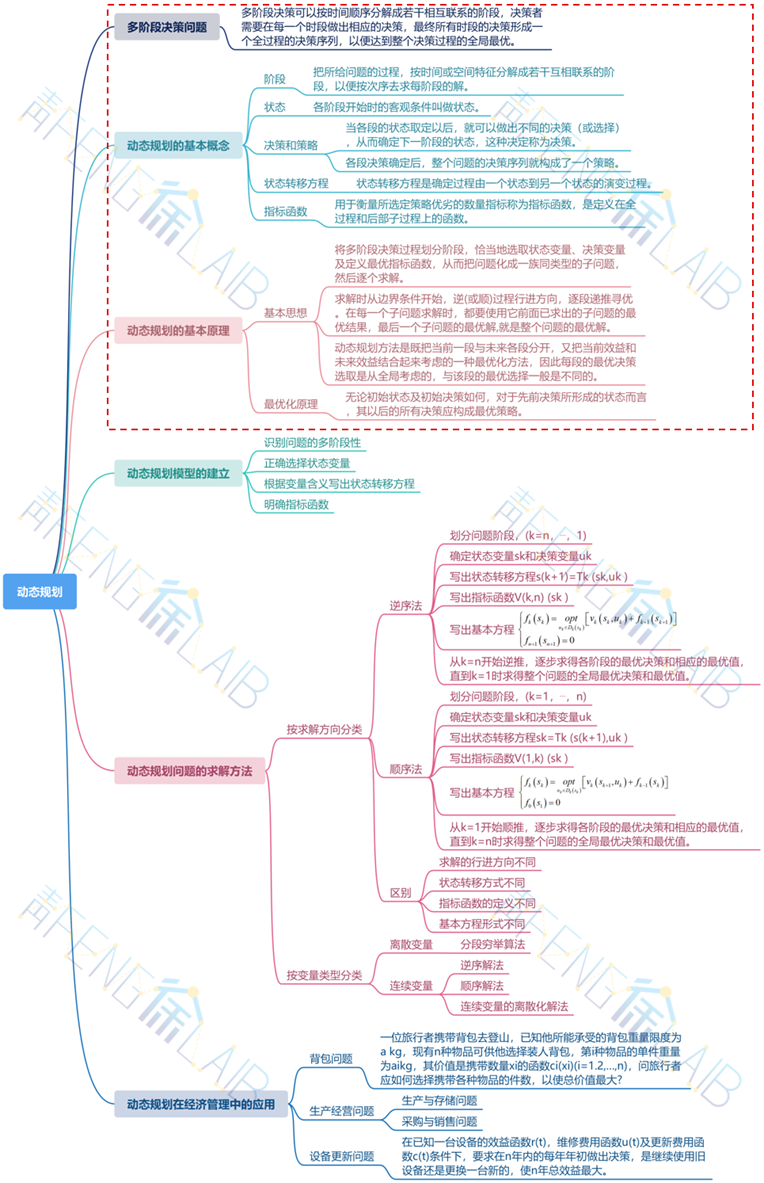
通过对动态规划问题基础知识进行梳理和总结，小编绘制了《动态规划思维导图》，如下图所示。动态规划问题章节一共有6个知识点。

第1个知识点是多阶段决策问题，对多阶段决策问题的概念进行了介绍。

第2个知识点是动态规划的基本概念，对将实际问题写成动态规划模型所用到的5个基本概念进行介绍。

第3个知识点是动态规划的基本原理，包括动态规划的基本思想和最优化原理。

第4个知识点和第5个知识点分别是动态规划模型的建立与求解，该部分阐述了动态规划模型的建立步骤，并重点介绍了顺序法、逆序法及其他求解常用算法。

第6个知识点是动态规划在经济管理中的应用，包括背包问题、生产经营问题和设备更新问题。

今天，小编先带大家学习多阶段决策问题及动态规划问题的基本概念和基本原理。

一、多阶段决策问题

多阶段决策是指这样一类特殊的决策过程，它可以按时间顺序分解成若干相互联系的时段或阶段，决策者需要在每一个时段做出相应的决策，最终所有时段的决策形成一个全过程的决策序列，以便达到整个决策过程的全局最优。由于各时段的决策间存在着有机的联系，某一时段的决策执行将影响到下一时段的决策制定，以至于最终影响全局的优化效果，所以在做每个时段的决策时，决策者不仅需要考虑本时段内的效果最优，还应该考虑该决策对最终优化目标的影响，从而做出能够达到全局最优的决策序列。

动态规划就是符合上述要求的一种多阶段决策优化方法。

二、动态规划的基本概念

使用动态规划方法解决多阶段决策问题，首先要将实际问题改写成动态规划模型，此时，要用到以下概念：

1、动态规划的基本概念

（1）阶段：把所给问题的过程，按时间或空间特征分解成若干互相联系的阶段，以便按次序去求每阶段的解，常用字母k表示阶段变量。

（2）状态：各阶段开始时客观条件，常用sk表示第k阶段的状态变量。

（3）决策和策略：当各段的状态取定以后，就可以做出不同的决策，从而确定下一阶段的状态，这种决定称为决策，常用uk(sk)表示第k阶段当状态为sk的决策变量；在实际问题中决策变量的取值往往在某一范围之内，此范围称为允许决策集合，常用Dk(sk)表示第k阶段从状态sk出发的允许决策集合。

各段决策确定后，整个问题的决策序列就构成一个策略，用 。对于每个实际问题，可供选择的策略有一定范围，称为允许策略集合，记作P1,n，使整个问题达到最有效果的策略就是最优策略。

（4）状态转移方程：状态转移方程是确定过程由一个状态到另一个状态的演变过程，记为sk+1=Tk(sk, uk)。

（5）指标函数和最优值函数：指标函数是用于衡量所选定策略优劣的数量指标，是定义在全过程和后部子过程上的函数，常用Vk,n表示，即Vk,n=Vk,n(sk, uk, sk+1,…, sn+1),k=1,2,…,n，动态规划中的指标函数应具有可分离性，并满足递推关系。

常用的指标函数包括：

①全过程或后部子过程指标是它所包含的各阶段指标的求和，即

②全过程或后部子过程指标是它所包含的各阶段指标的乘积，即

指标函数的最优值称为最优值函数，记为fk (sk)，它表示从第k阶段的状态sk开始到第n 阶段的终止状态的决策过程，在采取了最优策略后得到的指标函数值，即

其中“opt”是最优化（optimization）的缩写，可根据题意更换为 min 或 max。

2、例题

下面，小编将通过一个例题来对上述问题的基本概念进行详细的阐述。给定一个线路网络图，要从A地向F地铺设一条输油管道，各点间连线上的数字表示距离，问应选择什么路线，可使总距离最短？

（1）阶段

从A到F可以分成从A到B，从B到C，从C到D，从D到E，再从E到F。五个阶段。k=1,2,3,4,5

（2）状态

第一阶段状态为A，第二阶段有两个状态：B1和B2，以此类推。

状态变量s1的集合S1={A}；

状态变量s2的集合S2={B1, B2}；

状态变量s3的集合S3={C1, C2, C3, C4}；

状态变量s4的集合S4={D1, D2, D3}；

状态变量s5的集合S5={E1, E2}。

（3）决策和策略

例如从第二阶段的状态B1出发，可选择下一阶段的C1, C2, C3，即其允许决策集合为D2(B1)={C1, C2, C3, C4}；若我们决定选择C3，则可表示决策为u2(B1)=C3。

（4）状态转移方程

该问题的状态转移方程为sk+1= uk(sk)

（5）指标函数

该问题的指标函数为两点间的距离

三、动态规划的基本原理

1、最优化原理

动态规划方法基于贝尔曼（R.Bellman）等人提出的最优化原理，可以表述为：

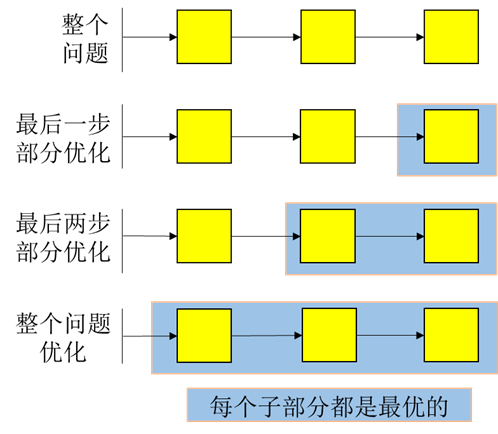
一个过程的最优策略具有这样的性质：即无论初始状态及初始决策如何，对于先前决策所形成的状态而言，其以后所有的决策应构成最优策略。换句话说，一个最优策略的子策略也是最优的。

2、基本思想

（1）例题引入

下面以最短路问题为例来介绍动态规划方法的基本思想。

例题：从A地到D地要铺设一条煤气管道，其中需经过两级中间站，两点之间的连线上的数字表示距离，如图所示。问应该选择什么路线，使总距离最短？

不难发现，根据最优化原理，如果A→M→N→E是起点A到终点D的一条最短路径，那么M→N→D必然也是从点M到终点D的最短路径。如果不是这样，则从点M到D必然存在另一条距离更短的路径M→N'→D，把它和A→M连接起来，就可以得到一条由A到D的新路径A→M→N'→D，它比原路径的行驶距离更短，这与假设矛盾。根据最短路问题的这一特点，可以从最后一段开始，采用由后向前逐步递推的方式，求出各点到E点的最短路径，直至最后求得由A到E的最短路径为止。

【求解过程】

将整个路径优化过程分为三个阶段A→B，B→C，C→D。从最后一个阶段开始计算，然后从后向前逐步推移至A点。

第三阶段（C→D）：k=3时，C有三条路线到终点D。

显然有f3(C1)=1；f3(C2)=3 ；f3(C3)=4

第二阶段（B→C）：k=2时，B有六条路线到C。

从状态B1出发，可得

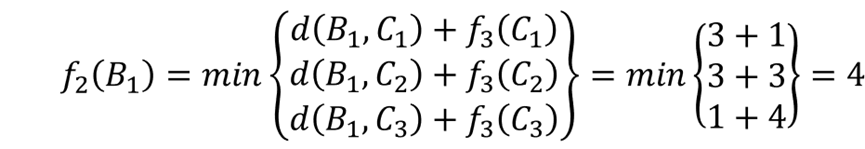
对应的最短路径为B1→C1→D。同理，从状态B2出发，可得

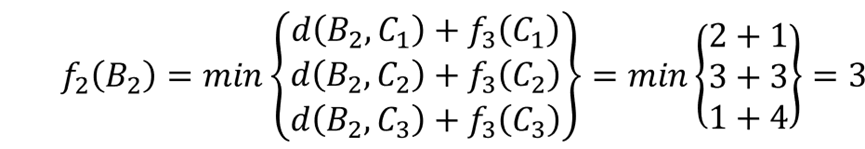
对应的最短路径为B2→C1→D。

第一阶段（A→B）：k=1时，A到B有两条路线。

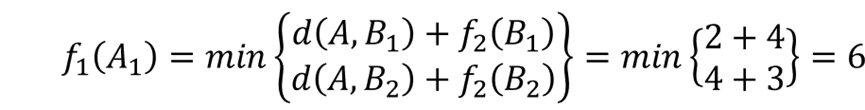
对应的最短路径为A→B1→C1→D，路长为6。

最短路线求解过程可以用一张图直观地表示出来。

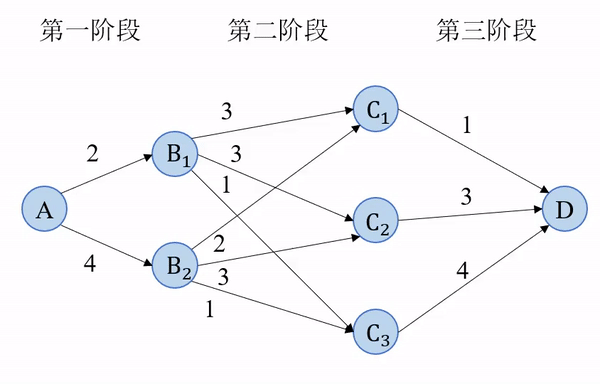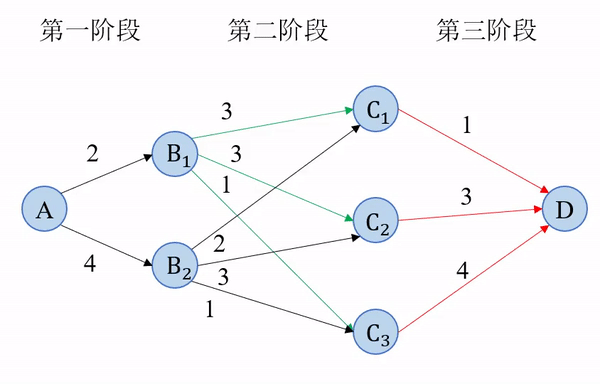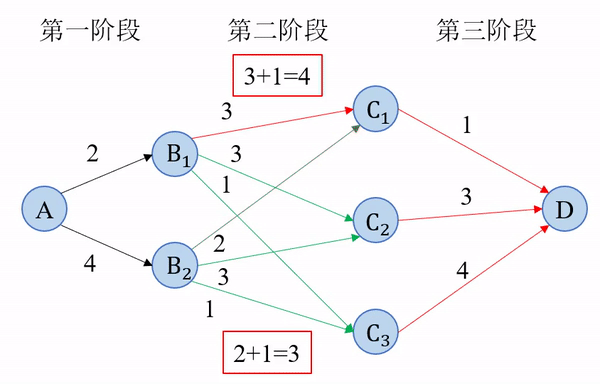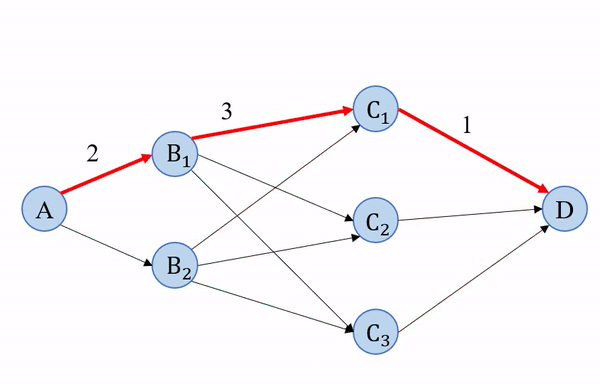
（2）最优方程

从例题的计算过程中可以看出，在求解的各阶段，都利用了第k段和第k+1段的如下关系：

其中， 为边界条件。

这种递推关系称为动态规划的基本方程，是根据最优性定理写出的。动态规划的基本方程是递推逐段求解的根据，一般来说，当指标函数为求和形式时，逆序求解的动态规划基本方程可以表示为上式。

（3）基本思想总结

①将多阶段决策过程划分阶段，恰当地选取状态变量、决策变量及定义最优指标函数，从而把问题化成一族同类型的子问题，然后逐个求解。

②求解时从边界条件开始，逆（或顺）过程行进方向，逐段递推寻优。在每一个子问题求解时，都要使用它前面已求出的子问题的最优结果，最后一个子问题的最优解，就是整个问题的最优解。

③动态规划方法是既把当前一段与未来各段分开，又把当前效益和未来效益结合起来考虑的一种最优化方法，因此每段的最优决策选取是从全局考虑的，与该段的最优选择一般是不同的。

3、小结

（1）利用最优化原理，可以把多阶段决策问题求解过程表示成一个连续的地推过程，由后向前逐步计算。在求解时，前面的各状态与决策，对后面的子过程来说，只相当于初始条件，并不影响后面子过程的最优决策。

（2）为了求出最短路线，一种简单的方法（穷举法）是求出所有从A到D的可能铺设的长度并加以比较。但当问题的阶段数很多、每段的状态也很多时，穷举法的计算量会大大增加，甚至使求优成为不可能。

相比之下，动态规划方法计算量小，而且计算结果不仅得到了全局最优的结果，也得到了中间任意一段的最优结果。

以上就是本期动态规划的全部内容啦，通过对这一期的学习，我们对动态规划有了初步的了解，大家也可以在日常生活中寻找多阶段决策问题的案例，并尝试用动态规划的思想去求解吧！