面试算法116：朋友圈

题目

假设一个班级中有n个学生。学生之间有些是朋友，有些不是。朋友关系是可以传递的。例如，A是B的直接朋友，B是C的直接朋友，那么A是C的间接朋友。定义朋友圈就是一组直接朋友或间接朋友的学生。输入一个n×n的矩阵M表示班上的朋友关系，如果M[i][j]=1，那么学生i和学生j是直接朋友。请计算该班级中朋友圈的数目。
例如，输入数组[[1，1，0]，[1，1，0]，[0，0，1]]，学生0和学生1是朋友，他们组成一个朋友圈；学生2一个人组成一个朋友圈。因此，该班级中朋友圈的数目是2。

分析

一个班级可以包含一个或多个朋友圈，对应的图中可能包含一个或多个子图，每个朋友圈对应一个子图。因此，这个问题可以转化为如何求图中子图的数目。
图的搜索算法可以用来计算图中子图的数目。扫描图中所有的节点。如果某个节点v之前没有访问过，就搜索它所在的子图。当所有节点都访问完之后，就可以知道图中有多少个子图。

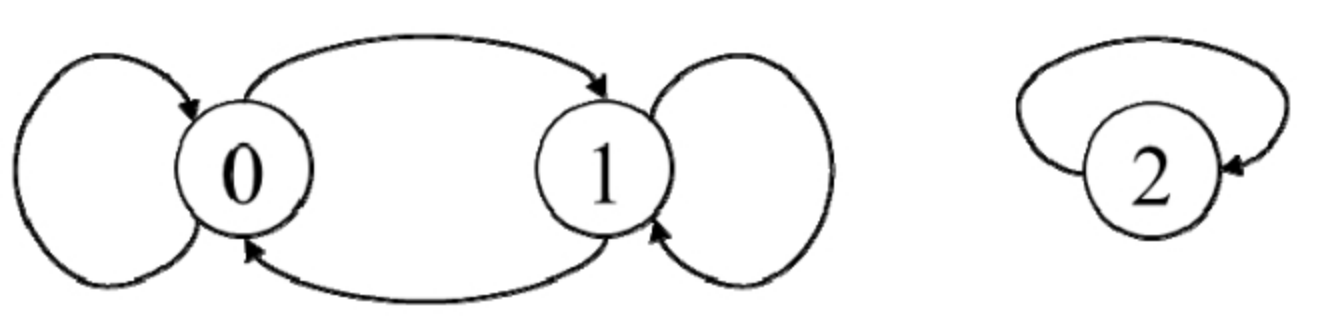
解：应用图搜索解决问题

public class Test {
    public static void main(String[] args) {
        int[][] M = {{1, 1, 0}, {1, 1, 0}, {0, 0, 1}};
        int result = findCircleNum(M);// 记录朋友圈的数目
        System.out.println(result);
    }

    public static int findCircleNum(int[][] M) {
        boolean[] visited = new boolean[M.length];
        int result = 0;
        for (int i = 0; i < M.length; i++) {
            if (!visited[i]) {
            	// 如果某个学生i对应的节点之前没有访问过，则调用函数findCircle访问他所在朋友圈对应子图的所有节点
                findCircle(M, visited, i);
                result++;
            }
        }

        return result;
    }

    private static void findCircle(int[][] M, boolean[] visited, int i) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(i);
        visited[i] = true;
        while (!queue.isEmpty()) {
            int t = queue.remove();
            for (int friend = 0; friend < M.length; friend++) {
                if (M[t][friend] == 1 && !visited[friend]) {
                    queue.add(friend);
                    visited[friend] = true;
                }
            }
        }
    }

}