UVa12304 2D Geometry 110 in 1!

题目链接

? ? ? ? ?UVa12304 2D Geometry 110 in 1!

题意

????????这是一个拥有6（二进制是110）个子问题的2D几何问题集。
????????1 CircumscribedCircle x1 y1 x2 y2 x3 y3：求三角形(x1,y1)-(x2,y2)-(x3,y3)的外接圆。这3点保证不共线。答案应格式化成(x,y,r)，表示圆心为(x,y)，半径为r。
????????2、InscribedCircle x1 y1 x2 y2 x3 y3：求三角形(x1,y1)-(x2,y2)-(x3,y3)的内切圆。这3点保证不共线。答案应格式化成(x,y,r)，表示圆心为(x,y)，半径为r。
????????3、TangentLineThroughPoint xc yc r xp yp：给定一个圆心在(xc,yc)，半径为r 的圆，求过点(xp,yp)并且和这个圆相切的所有切线。每条切线格式化为angle，表示直线的极角（角度，0≤angle＜180）。整个答案应格式化为列表（见后）。如果无解，应打印空列表。
????????4、CircleThroughAPointAndTangentToALineWithRadius xp yp x1 y1 x2 y2 r：求出所有经过点(xp,yp)并且和直线(x1,y1)-(x2,y2)相切的半径为r 的圆。每个圆格式化为(x,y)，因为半径已经给定。整个答案应格式化为列表（同上）。?
????????5、CircleTangentToTwoLinesWithRadius x1 y1 x2 y2 x3 y3 x4 y4 r：给出两条不平行直线(x1,y1)-(x2,y2)和(x3,y3)-(x4,y4)，求所有半径为r 并且同时和这两条直线相切的圆。每个圆格式化为(x,y)，因为半径已经给定。整个答案应格式化为列表（同上）。
????????6、CircleTangentToTwoDisjointCirclesWithRadius x1 y1 r1 x2 y2 r2 r：给定两个相离的圆(x1,y1,r1)和(x2,y2,r2)，求出所有和这两个圆外切的，半径为r 的圆。注意，因为是外切，求出的圆不能把这两个给定圆包含在内部。每个圆格式化为(x,y)，因为半径已经给定。整个答案应格式化为列表（同上）。
????????对于上述所有直线，输入的两个点保证不重合。当格式化实数列表时，所有数应从小到大排列；当格式化二元组(x,y)时，先按x 从小到大排序，当x 相同时按y 从小到大排序。

分析

????????第一个问题设外接圆的圆心坐标为x、y，半径为r，列方程组求解。

????????第二个问题利用内心坐标公式求解：设的顶点坐标分别为、、，三个角对应的边长分别为a、b、c，则内心坐标为。求得内心坐标后再求一下它与三角形某条边的距离即可得到内切圆半径。

????????第三个子问题切线格式化为极角要注意反三角函数的值域，最后一定要确保在。

? ? ? ?《训练指南》上讲第四、五、六个问题的解法：

????????第四个问题：因为已知半径为r，所以要想和直线L相切，圆心到直线的距离一定为r。满足这个条件的点的轨迹是两条直线。而要想过定点，圆心点该点的距离一定为r，满足这个条件的点的轨迹是一个圆。求出圆和这两条直线的交点即可。

????????第五个问题解法类似，根据每条直线得到两条新直线，再两两求交点即可。
????????第六个问题解法也类似，根据两个圆得到两个新的圆，求交点即可。

? ? ? ? 这里说一下第五、六两个问题的直接几何解法：

????????第五个问题：求出两直线的交点P，以及pc与两条直线的夹角α，则，并且将某直线的方向向量旋转α角就得到pc的方向向量，由此算出一个C，pc的方向向量再依次旋转90度三下可以算出另外三个C点，要注意旋转90度和270度时pc长度变了（）。

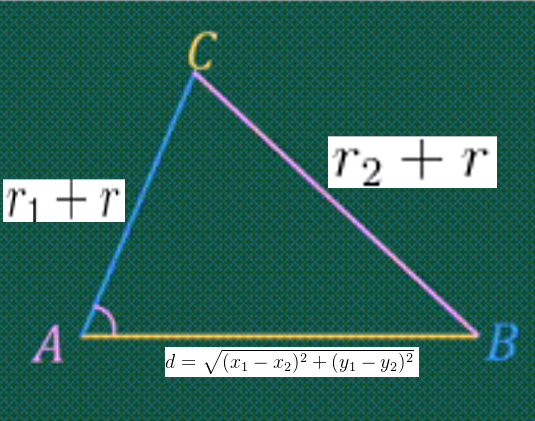
????????第六个问题：本质是求下图的C点坐标，借助余弦定理把∠ A求出，然后将AB的方向向量旋转∠ A就得到AC的方向向量，进而算出C点坐标。

AC代码

#include <iostream>
#include <cmath>
#include <iomanip>
#include <algorithm>
using namespace std;

#define eps 1e-10
struct Point {
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) {}
    void Normalize() {
        double l = sqrt(x*x + y*y); x /= l; y /= l;
    }
};
typedef Point Vector;

Vector operator+ (Vector A, Vector B) {
    return Vector(A.x + B.x, A.y + B.y);
}
 
Vector operator- (Point A, Point B) {
    return Vector(A.x - B.x, A.y - B.y);
}
 
Vector operator* (Vector A, double p) {
    return Vector(A.x * p, A.y * p);
}
 
Vector operator/ (Vector A, double p) {
    return Vector(A.x / p, A.y / p);
}
 
bool operator< (const Point& a, const Point& b) {
    return a.x < b.x || (a.x == b.x && a.y < b.y);
}
 
int dcmp(double x) {
    return abs(x) < eps ? 0 : (x < 0 ? -1 : 1);
}
 
double Dot(Vector A, Vector B) {
    return A.x * B.x + A.y * B.y;
}
 
double Length(Vector A) {
    return sqrt(Dot(A, A));
}
 
double Angle(Vector A, Vector B) {
    return acos(Dot(A, B) / Length(A) / Length(B));
}
 
double Cross(Vector A, Vector B) {
    return A.x * B.y - A.y * B.x;
}

Vector Rotate(Vector A, double rad) {
    return Vector(A.x * cos(rad) - A.y * sin(rad), A.x * sin(rad) + A.y * cos(rad));
}

Vector Normal(Vector A) {
    double L = Length(A);
    return Vector(-A.y / L, A.x / L);
}
 
Point GetLineIntersection(Point P, Vector v, Point Q, Vector w) {
    Vector u = P - Q;
    double t = Cross(w, u) / Cross(v, w);
    return P + v * t;
}

double DistanceToLine(Point P, Point A, Point B) {
    Vector v1 = B - A, v2 = P - A;
    return abs(Cross(v1, v2)) / Length(v1);
}

void solveU() {
    double x1, y1, x2, y2, x3, y3; cin >> x1 >> y1 >> x2 >> y2 >> x3 >> y3;
    double x = ((x1*x1+y1*y1)*(y2-y3) + (x2*x2+y2*y2)*(y3-y1) + (x3*x3+y3*y3)*(y1-y2)) /
                ((y1-y3)*(x1-x2) - (y1-y2)*(x1-x3)) / 2;
    double y = ((x1*x1+y1*y1)*(x2-x3) + (x2*x2+y2*y2)*(x3-x1) + (x3*x3+y3*y3)*(x1-x2)) /
                ((x1-x3)*(y1-y2) - (x1-x2)*(y1-y3)) / 2;
    cout << '(' << x << ',' << y << ',' << sqrt((x-x1)*(x-x1) + (y-y1)*(y-y1)) << ')' << endl;
}

void solveI() {
    Point p1, p2, p3; cin >> p1.x >> p1.y >> p2.x >> p2.y >> p3.x >> p3.y;
    double a = Length(p2-p3), b = Length(p3-p1), c = Length(p1-p2); Point p = (p1*a+p2*b+p3*c)/(a+b+c);
    cout << '(' << p.x << ',' << p.y << ',' << DistanceToLine(p, p1, p2) << ')' << endl;
}

void solveT() {
    int x, y, r, xp, yp; cin >> x >> y >> r >> xp >> yp;
    int d = (x-xp)*(x-xp) + (y-yp)*(y-yp) - r*r;
    if (d < 0.) {
        cout << "[]" << endl; return;
    } else if (d == 0) {
        double a = 180*atan2(yp-y, xp-x)/M_PI; a = a<0 ? a + 450 : a + 90;
        cout << '[' << (dcmp(a-360)>=0 ? a-360 : (dcmp(a-180)>=0 ? a-180 : a)) << ']' << endl; return;
    } else {
        double a = 180*atan2(yp-y, xp-x)/M_PI, b = 180*asin(r/sqrt((x-xp)*(x-xp) + (y-yp)*(y-yp)))/M_PI;
        if (a < 0) a += 360;
        double x = a + b, y = a<b ? 180+a-b : a-b;
        x = dcmp(x-360)>=0 ? x-360 : (dcmp(x-180)>=0 ? x-180 : x);
        y = dcmp(y-360)>=0 ? y-360 : (dcmp(y-180)>=0 ? y-180 : y);
        cout << '[' << min(x, y) << ',' << max(x, y) << ']' << endl;
    }
}

void solveA() {
    int xp, yp, x1, y1, x2, y2, r; cin >> xp >> yp >> x1 >> y1 >> x2 >> y2 >> r;
    if ((xp-x1)*(yp-y2) == (xp-x2)*(yp-y1)) {
        double a = atan2(x2-x1, y1-y2);
        Point p1(xp + r*cos(a), yp + r*sin(a)), p2(xp - r*cos(a), yp - r*sin(a)), t;
        if (p2 < p1) t = p1, p1 = p2, p2 = t;
        cout << "[(" << p1.x << ',' << p1.y << "),(" << p2.x << "," << p2.y << ")]" << endl;
    } else {
        Point a(x1, y1), b(x2, y2); Vector v = Normal(Vector(x2-x1, y2-y1));
        double d = DistanceToLine(Point(xp, yp), a, b);
        Point p(xp + v.x * r, yp + v.y * r);
        if (d > 2*r) {
            cout << "[]" << endl;
        } else if (d == 2*r) {
            if (DistanceToLine(p, a, b) > 2*r) p.x = xp - v.x * r, p.y = yp - v.y * r;
            cout << "[(" << p.x << ',' << p.y << ")]" << endl;
        } else {
            double d1 = DistanceToLine(p, a, b);
            if ((d<r && dcmp(d1+d-r) == 0) || (d>r && dcmp(d1+r-d) == 0)) v.x = -v.x, v.y = -v.y;
            double a = atan2(v.y, v.x), b = acos((r-d)/r);
            Point p1(xp + r*cos(a+b), yp + r*sin(a+b)), p2(xp + r*cos(a-b), yp + r*sin(a-b)), t;
            if (p2 < p1) t = p1, p1 = p2, p2 = t;
            cout << "[(" << p1.x << ',' << p1.y << "),(" << p2.x << "," << p2.y << ")]" << endl;
        }
    }
}

void solveL() {
    Point p1, p2, p3, p4; int r; cin >> p1.x >> p1.y >> p2.x >> p2.y >> p3.x >> p3.y >> p4.x >> p4.y >> r;
    Vector v = p2-p1, w = p4-p3; Point p = GetLineIntersection(p1, v, p3, w); double a = Angle(v, w) / 2;
    v.Normalize(); v = Rotate(v, Cross(v, w) < 0. ? -a : a);
    double r1 = r / sin(a), r2 = r / cos(a);
    Point c[] = {Point(p.x + v.x*r1, p.y + v.y*r1), Point(p.x - v.x*r1, p.y - v.y*r1),
                 Point(p.x - v.y*r2, p.y + v.x*r2), Point(p.x + v.y*r2, p.y - v.x*r2)};
    sort(c, c+4);
    cout << "[(" << c[0].x << ',' << c[0].y << "),(" << c[1].x << "," << c[1].y << "),("
         << c[2].x << ',' << c[2].y << "),(" << c[3].x << "," << c[3].y << ")]" << endl;
}

void solveD() {
    int x1, y1, r1, x2, y2, r2, r; cin >> x1 >> y1 >> r1 >> x2 >> y2 >> r2 >> r;
    double d = sqrt((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2)); Vector v(x2-x1, y2-y1); int cmp = dcmp(d - r1 - r2 - 2*r);
    if (cmp > 0 || (dcmp(d+min(r1,r2)-max(r1,r2)) < 0)) {
        cout << "[]" << endl;
    } else if (cmp == 0) {
        double t = (r1+r) / d;
        cout << "[(" << x1 + v.x * t << ',' << y1 + v.y * t << ")]" << endl;
    } else {
        double a = acos(((r+r1)*(r+r1) + d*d - (r+r2)*(r+r2)) / (r+r1) / d / 2);
        v.Normalize(); Vector w = Rotate(v, -a); v = Rotate(v, a);
        Point p1(x1 + v.x*(r+r1), y1 + v.y*(r+r1)), p2(x1 + w.x*(r+r1), y1 + w.y*(r+r1)), t;
        if (p2 < p1) t = p1, p1 = p2, p2 = t;
        cout << "[(" << p1.x << ',' << p1.y << "),(" << p2.x << "," << p2.y << ")]" << endl;
    }
}

char s[48];

void solve() {
    if (s[0] == 'I') solveI();
    else if (s[0] == 'T') solveT();
    else if (s[4] == 'u') solveU();
    else if (s[13] == 'A') solveA();
    else if (s[18] == 'L') solveL();
    else solveD();
}

int main() {
    cout << fixed << setprecision(6);
    while (cin >> s) solve();
    return 0;
}