pat 甲级 1007 Maximum Subsequence Sum

这道题是一道dp题。将问题拆解成两步：1.如何求得最大子序列和。2.如何求得最大子序列的第一个和最后一个数字，并保证如果最大子序列不是唯一的，则输出索引i和j最小的子系列。

1.如何求得最大子序列和？

首先定义一个集合f[i]，表示以i为右端点的区间和的最大值（即i之前并包含i的最大子序列和）。可以将集合进行划分，如下图所示.

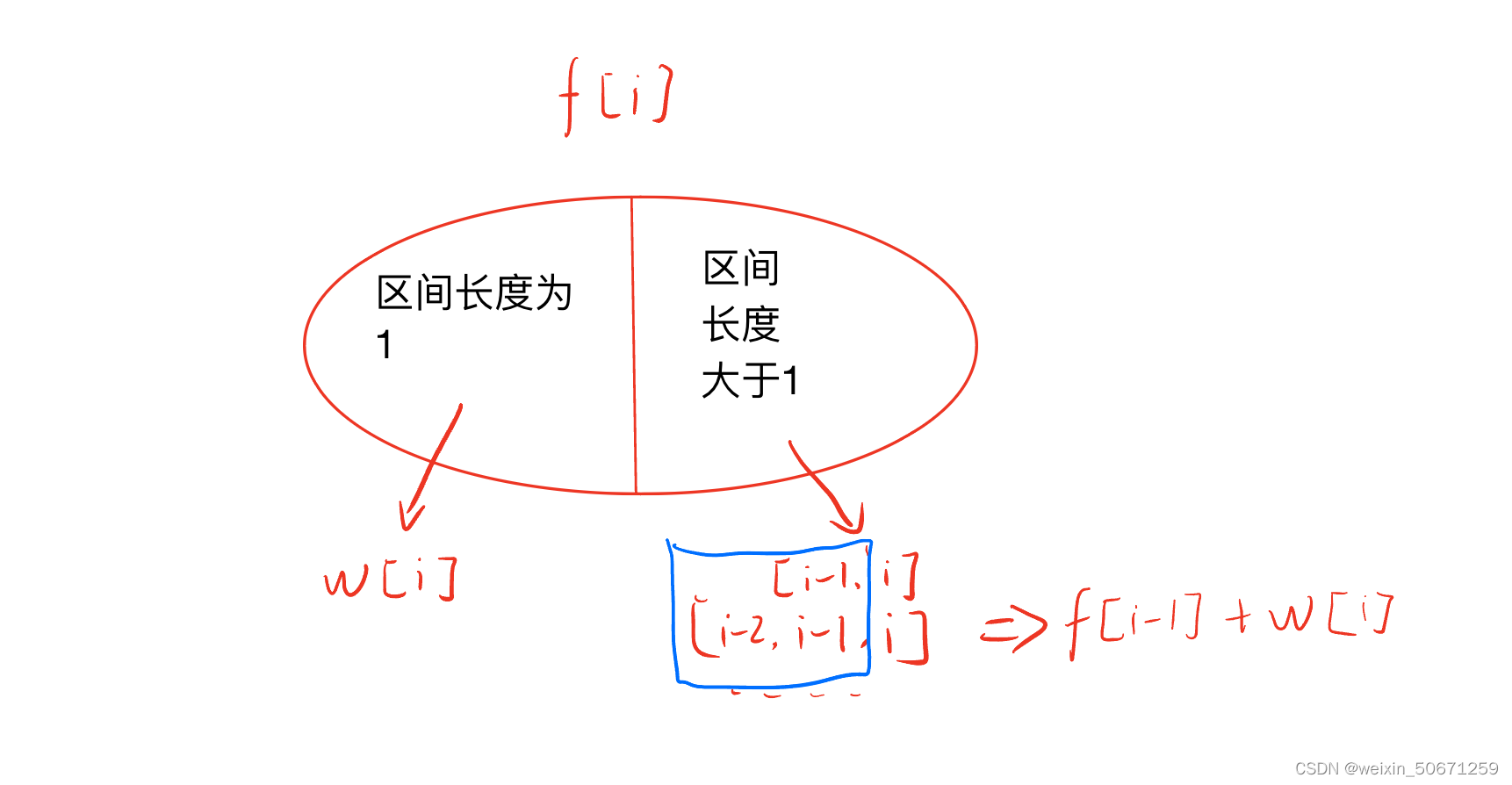
（1）当区间长度取1时（取i），f[i]=w[i](即i的值）;(2) 当区间长度大于1时，i必取，则f[i]=f[i-1]+w[i];(3)最大子序列和，故取（1）(2)的max。f[i]=max(w[i],f[i-1]+w[i])=w[i]+max(0,f[i-1]);

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;
const int N=10010;
int w[N];

int main()
{
    int k;
    cin>>k;
    for(int i=1;i<=k;i++){
        cin>>w[i];
    }
    int res=-1;
    for(int i=1,f=0;i<=k;i++){ 
        f=w[i]+max(0,f);//因为f[i]只有一个变量，可以用f代替，相当于f[i]=w[i]+max(0,f[i-1])
        res=max(res,f);
    }  
    cout<<res<<endl;
    return 0;
}

2.如何求得最大子序列的第一个和最后一个数字，并保证如果最大子序列不是唯一的，则输出索引i和j最小的子系列？

用l，r记录最大子序列的第一个和最后一个数字。具体处理方式看代码

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;
const int N=10010;
int w[N];

int main()
{
    int k;
    cin>>k;
    for(int i=1;i<=k;i++){
        cin>>w[i];
    }
    int res=-1,l,r;
    for(int i=1,f=-1,start;i<=k;i++){//start记录第一个数字
      //f=w[i]+max(0,f); 
        if(f<0) f=0,start=i;
        f+=w[i]; //这两行与f=w[i]+max(0,f)作用相同；当f<0时，意味着f=w[i],子序列长度为1，故start=i
        // res=max(res,f);
        if(res<f){
            res=f;
            l=w[start],r=w[i];//记录第一个和最后一个数字
        }
       
    }  
    if(res<0) res=0,l=w[1],r=w[k];//处理题目中的特殊情况
    cout<<res<<" "<<l<<" "<<r<<endl;
    return 0;
}