损失函数，代价函数，梯度，优化器，学习率，学习率调度器

这些是机器学习中的概念。把这些概念迁移到CV领域要进行一定的抽象。

首先损失，损失是一组参数拟合出来的样本的预测值和样本的真实值之间的差异，损失是用来度量这种差异的，根据不同的拟合权重参数全局有一个对应的损失值，损失后续经过反向传播计算每个参数对应的梯度，找出一个梯度下降最快的方向，用不同的学习率作为优化步长和不同策略的优化器进行优化，所以如何来计算损失对于模型最后的优化效果非常重要。对于梯度，梯度方向，梯度方向是模型代价函数下降最快的方向，代价函数是 损失-权重参数 的一个函数关系，根据参数的不同，可以是一个任意的曲线，可以是一个任意的曲面，更多参数就是无法可视化的高维复杂的函数，整体概念是差不多的。学习率是参数一次更新的步长，学习率调度器是根据一些指标进行学习率的改变，改变优化器优化的步长。优化器的选择也是一个问题，从之前的BGD,到SGD，MBGD，AdaGrad，RMSProp,AdaDelta,Adam,Monmentum等，有全局最优，局部最优的问题，还有震荡的问题。pytorch也提供了六种学习率调度策略，分别是等间隔法，给定间隔法，指数衰减法，余弦下降法，监控指标调整法，LambdaLR自定义调整策略。（有序调整，自适应调整，自定义调整），微调模型设置较小的学习率，从0训练设置较大的学习率。

学习率(Learning rate)作为监督学习以及深度学习中重要的超参，其决定着目标函数能否收敛到局部最小值以及何时收敛到最小值。合适的学习率能够使目标函数在合适的时间内收敛到局部最小值。

正则化，减小方差的策略。解决过拟合问题，过拟合就是说在训练集上方差很小，基本完全拟合，但是在验证集上方差很大，正则化就是降低这个方差，也就是解决模型的过拟合问题。

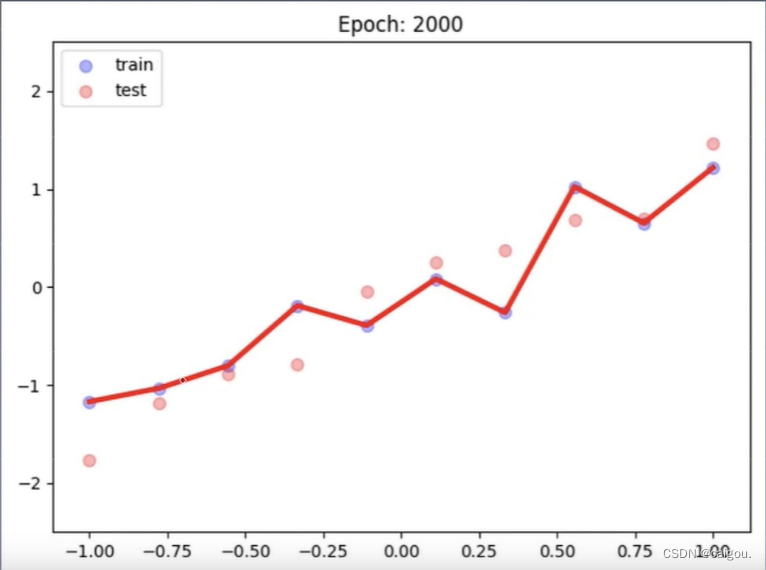
以上训练过程都是尽量的降低损失，但是在训练集上损失降的过低，会产生过拟合问题，模型泛化能力降低。所以要考虑的是不同权重的参数组合造成的损失等高线和L1正则项都要最小，

随着海量数据处理的兴起，工程上对于模型稀疏化的要求也随之出现了。这时候，L2正则化已经不能满足需求，因为它只是使得模型的参数值趋近于0，而不是等于0，这样就无法丢掉模型里的任何一个特征，因此无法做到稀疏化。这时，L1的作用随之显现。L1正则化的作用是使得大部分模型参数的值等于0，这样一来，当模型训练好后，这些权值等于0的特征可以省去，从而达到稀疏化的目的，也节省了存储的空间，因为在计算时，值为0的特征都可以不用存储了。

L1在确实需要稀疏化模型的场景下，才能发挥很好的作用并且效果远胜于L2。在模型特征个数远大于训练样本数的情况下，如果我们事先知道模型的特征中只有少量相关特征（即参数值不为0），并且相关特征的个数少于训练样本数，那么L1的效果远好于L2。然而，需要注意的是，当相关特征数远大于训练样本数时，无论是L1还是L2，都无法取得很好的效果。

L1正则化：得到满足上面情况的解发生在坐标轴上，特点是 0参数，产生稀疏项，

L2正则化：又称weight decay(权值衰减),知道带上权值衰减就是L2正则化就行了，是定义在优化器里的一个参数，weight_decay就是找一个平衡，不至于过度追求损失的降低。让权值参数不断减小。防止过拟合现象。

optim_normal = torch.optim.SGD(net_normal.parameters(), lr=lr_init, momentum=0.9)
optim_wdecay = torch.optim.SGD(net_weight_decay.parameters(), lr=lr_init, momentum=0.9, weight_decay=1e-2)

动量：用势能来理解。避免模型陷入局部最优点。

学习率调度方法：

等间隔

 from torch.optim.lr_scheduler import StepLR
 
 scheduler = StepLR(optimizer, 
                    step_size = 4, # Period of learning rate decay
                    gamma = 0.5) # Multiplicative factor of learning rate decay

?给定间隔

 from torch.optim.lr_scheduler import MultiStepLR
 
 scheduler = MultiStepLR(optimizer, 
                         milestones=[8, 24, 28], # List of epoch indices
                         gamma =0.5) # Multiplicative factor of learning rate decay

?指数衰减

 rom torch.optim.lr_scheduler import ExponentialLR
 
 scheduler = ExponentialLR(optimizer, 
                           gamma = 0.5) # Multiplicative factor of learning rate decay.

?余弦调度

 from torch.optim.lr_scheduler import CosineAnnealingLR
 
 scheduler = CosineAnnealingLR(optimizer,
                               T_max = 32, # Maximum number of iterations.
                              eta_min = 1e-4) # Minimum learning rate.

?监控指标调度ReduceLROnPlateauLR

? ? ? ? 注意这个调度器的参数，mode是指根据监测指标不下降（如损失）就进行学习率调度或不增大（如准确率）就调度。要注意的是，一般学习率一个epoch调整一次，调整时候实例化的调度器

scheduler.step(loss_value) 的step()调度方法里要传入监测的指标。??

ReduceLROnPlateauLR的参数，facyor:调整系数，patience:接受几次不变化，cooldown:冷却时间，停止监控一段时间，verbose:是否打印日志，min_lr:学习率下限，eps:学习率衰减最小值。

import torch
from torch import nn, optim
from torch.optim.lr_scheduler import ReduceLROnPlateau

python复制代码# 创建模型实例
model = Net()

# 定义损失函数
criterion = nn.MSELoss()

# 定义优化器和学习率
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 定义学习率调度器
scheduler = ReduceLROnPlateau(optimizer, mode='min', factor=0.1, patience=5)

自定义调整策略

import torch
import matplotlib.pyplot as plt
 
 
epoches = 100
learning_rate = 0.1
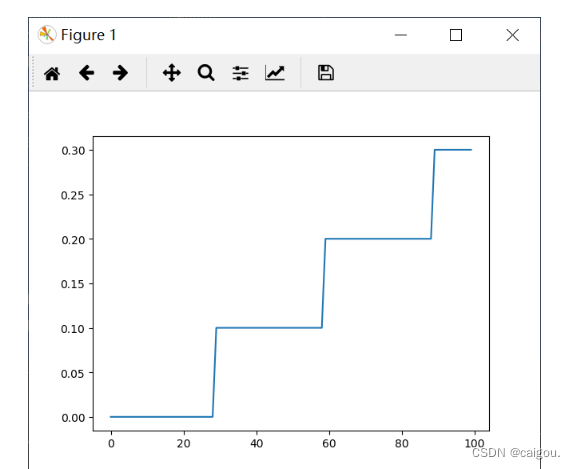
lambda1 = lambda epoch: epoch // 30
lambda2 = lambda epoch: 0.95 ** epoch
model = [torch.nn.Parameter(torch.randn(2, 2, requires_grad=True))]
optimizer = torch.optim.SGD(model, learning_rate)
scheduler = torch.optim.lr_scheduler.LambdaLR(optimizer=optimizer, lr_lambda=[lambda1])
e = [i for i in range(epoches)]
lrs = []
for epoch in range(100):
    optimizer.step()
    scheduler.step()
    lrs.append(scheduler.get_last_lr())
 
plt.plot(e, lrs)
plt.show()
 

?

 
import torch
import torch.utils.data as Data
import torch.nn.functional as F
from torch.autograd import Variable
import matplotlib.pyplot as plt
 
# 超参数
LR = 0.01
BATCH_SIZE = 32
EPOCH = 12
 
# 生成假数据
# torch.unsqueeze() 的作用是将一维变二维，torch只能处理二维的数据
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)  # x data (tensor), shape(100, 1)
# 0.2 * torch.rand(x.size())增加噪点
y = x.pow(2) + 0.1 * torch.normal(torch.zeros(*x.size()))
 
# 定义数据库
dataset = Data.TensorDataset(x, y)
 
# 定义数据加载器
loader = Data.DataLoader(dataset=dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=0)
 
 
# 定义pytorch网络
class Net(torch.nn.Module):
    def __init__(self, n_features, n_hidden, n_output):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_features, n_hidden)
        self.predict = torch.nn.Linear(n_hidden, n_output)
 
    def forward(self, x):
        x = F.relu(self.hidden(x))
        y = self.predict(x)
        return y
 
# 定义不同的优化器网络
net_SGD = Net(1, 10, 1)
net_Momentum = Net(1, 10, 1)
net_Adagrad = Net(1, 10, 1)
net_Adadelta = Net(1, 10, 1)
net_RMSprop = Net(1, 10, 1)
net_Adam = Net(1, 10, 1)
net_Adamax = Net(1, 10, 1)
net_AdamW = Net(1, 10, 1)
net_LBFGS = Net(1, 10, 1)
 
# 选择不同的优化方法
opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.9)
opt_Adagrad = torch.optim.Adagrad(net_Adagrad.parameters(), lr=LR)
opt_Adadelta = torch.optim.Adadelta(net_Adadelta.parameters(), lr=LR)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
opt_Adamax = torch.optim.Adamax(net_Adamax.parameters(), lr=LR, betas=(0.9, 0.99))
opt_AdamW = torch.optim.AdamW(net_AdamW.parameters(), lr=LR, betas=(0.9, 0.99))
opt_LBFGS = torch.optim.LBFGS(net_LBFGS.parameters(), lr=LR, max_iter=10, max_eval=10)
 
 
 
nets = [net_SGD, net_Momentum, net_Adagrad, net_Adadelta, net_RMSprop, net_Adam, net_Adamax, net_AdamW, net_LBFGS]
optimizers = [opt_SGD, opt_Momentum, opt_Adagrad, opt_Adadelta, opt_RMSprop, opt_Adam, opt_Adamax, opt_AdamW, opt_LBFGS]
 
# 选择损失函数
loss_func = torch.nn.MSELoss()
 
# 不同方法的loss
loss_SGD = []
loss_Momentum = []
loss_Adagrad = []
loss_Adadelta = []
loss_RMSprop = []
loss_Adam = []
loss_Adamax = []
loss_AdamW = []
loss_LBFGS = []
 
# 保存所有loss
losses = [loss_SGD, loss_Momentum, loss_Adagrad, loss_Adadelta, loss_RMSprop, loss_Adam, loss_Adamax, loss_AdamW, loss_LBFGS]
 
# 执行训练
for epoch in range(EPOCH):
    for step, (batch_x, batch_y) in enumerate(loader):
        var_x = Variable(batch_x)
        var_y = Variable(batch_y)
        for net, optimizer, loss_history in zip(nets, optimizers, losses):
            if isinstance(optimizer, torch.optim.LBFGS):
                def closure():
                    y_pred = net(var_x)
                    loss = loss_func(y_pred, var_y)
                    optimizer.zero_grad()
                    loss.backward()
                    return loss
                loss = optimizer.step(closure)
            else:
                # 对x进行预测
                prediction = net(var_x)
                # 计算损失
                loss = loss_func(prediction, var_y)
                # 每次迭代清空上一次的梯度
                optimizer.zero_grad()
                # 反向传播
                loss.backward()
                # 更新梯度
                optimizer.step()
            # 保存loss记录
            loss_history.append(loss.data)
 
# 画图
labels = ['SGD', 'Momentum', 'Adagrad', 'Adadelta', 'RMSprop', 'Adam', 'Adamax', 'AdamW', 'LBFGS']
for i, loss_history in enumerate(losses):
    plt.plot(loss_history, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0, 0.2))
plt.show()
 

参考博客：https://blog.csdn.net/xian0710830114/article/details/126551268