数据结构：并差集

1.并查集（Union Find）：

一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。不交集指的是一系列没有重复元素的集合。

简单来说，并查集就是用来处理集合的合并和集合的查询。

并查集中的「集」指的就是我们初中所学的集合概念，在这里指的是不相交的集合，即一系列没有重复元素的集合。

并查集中的「并」指的就是集合的并集操作，将两个集合合并之后就变成一个集合。合并操作如下所示：{1, 3, 5, 7} ∪ {2, 4, 6, 8} = {1, 2, 3, 4, 5, 6, 7, 8}

并查集中的「查」是对于集合中存放的元素来说的，通常我们需要查询两个元素是否属于同一个集合。

如果我们只是想知道一个元素是否在集合中，可以通过 Python 或其他语言中的 set 集合来解决。而如果我们想知道两个元素是否属于同一个集合，则仅用一个 set 集合就很难做到了。这就需要用到我们接下来要讲解的「并查集」结构。

根据上文描述，我们就可以定义一下「并查集」结构所支持的操作接口：

合并 union(x, y)：将集合 x 和集合 y 合并成一个集合。

查找 find(x)：查找元素 x 属于哪个集合。

查找 is_connected(x, y)：查询元素 x 和 y 是否在同一个集合中

2.算法例子：（用来判断是否存在一个环.）

判断下面树形数据结构是否有环，图为：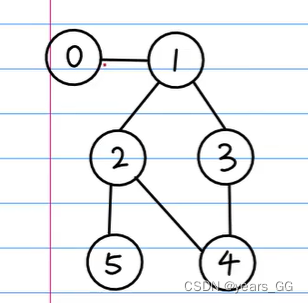
?

把它能够相连的数放入一个集合里面，如下图：

把两个集合合并，我们任意取两个节点，如果这两个节点在集合中，则说明该两个节点会形成环。

此时我们判断两个节点是否会形成环的话，就通过判断集合中是否存在这两个节点，如2和4在集合中会形成环。5和4一个在集合，一个不在则不会形成环?。

3.实现方法：

那么我们怎么把两个集合合并为一个集合呢？以及怎么用代码实现呢？

1. 我们构造一个树，用数组表示。默认全为-1.以上个例子为例，应该分成一个大小为6的数组，其下标为0,1,2,3,4,5.

2. 那么以上个例子为例，建一个数组parent，在数组中，我们给下标为1和2的数组元素赋值为0，表示0和2节点指向1。parent[0] = 1;parent[2] = 1;表示,1为父节点。此时它们相连（图1）。同理parent[3]=4;（图2）

?

3-1.我们把它们父节点连起来，即parent[1]=4;

3-2.此时我们判断2和4是否相连会形成环，就判断2和4的父节点是否相同，这个例子中，我们看到2和4的父节点都为4，说明它们相连会形成环。

4.代码实现：

假设我们有两个数root_x和root_y.则代表我们要把两个树的某一个节点x或者y相连，则需要把两个父节点相连。

?于是我们定义两个函数find_root() 和union()，表示查找根节点和合并两个数，并动态更新parent数组：

#include<iostream>
#include<vector>
using namespace std;
#define JIE_DIAN 6

int find_root(int x, vector<int>& parent) { // 注意这里使用引用传递
    int x_root = x;
    while (parent[x_root] != -1) {
        x_root = parent[x_root];
    }
    return x_root;
}

/* 当合并成功我们返回1，当两个节点在一个集合中返回0 */
int union_vertices(int x, int y, vector<int>& parent) { // 注意这里使用引用传递
    int x_root = find_root(x, parent);
    int y_root = find_root(y, parent);
    if (x_root == y_root) {
        return 0;
    } else {
        parent[x_root] = y_root;
        return 1;
    }
}

int main() {
    vector<int> parent(JIE_DIAN, -1); // 把默认值设置为-1
    vector<pair<int, int>> edges = {{0, 1}, {1, 2}, {1, 3}, {2, 4}, {3, 4}, {2, 5}};

    bool has_cycle = false;
    for (auto& edge : edges) {
        int x = edge.first;
        int y = edge.second;
        // 判断是否有环
        if (find_root(x, parent) == find_root(y, parent)) {
            cout << "have" << endl;
            has_cycle = true;
            break;
        } else {
            union_vertices(x, y, parent);
        }
        /*关于else：在给定的边 (x, y) 中，如果 x 和 y 的根节点相同，那么它们已经在同一个集合中，
        如果此时再合并这两个节点，就会形成一个环。但是，如果它们的根节点不同，说明它们目前不在同一个集合中，
        可以安全地合并它们而不会形成环。*/
    }
    
    if (!has_cycle) {
        cout << "not have" << endl;
    }
    return 0;
}
/*在其中我遇到的问题，由于原视频是用c写的，我希望自己用C++实现，但是在学习和变换的过程中我遇到了一些问题，但是都解决了
1.关于这个算法，我们在原视频中需要修改相应的参数，但我这里用了增强for循环避免了，因此我们判断一个图是否有环，只需要修改edges数组的值。
2.关于这个算法的parent数组的修改匹配，我其实是不了解的，因为作者也没说这个在合并的时候，通过边就可以实现动态的修改parent数组，
因此我在修改的时候很好的理解，并做出了改进。
3.该代码我测试了，结果是正确的。如果有任何问题，希望你提醒我,谢谢！
*/

?

/*在其中我遇到的问题，由于原视频是用c写的，我希望自己用C++实现，但是在学习和变换的过程中我遇到了一些问题，但是都解决了

1.关于这个算法，我们在原视频中需要修改相应的参数，但我这里用了增强for循环避免了，因此我们判断一个图是否有环，只需要修改edges数组的值。

2.关于这个算法的parent数组的修改匹配，我其实是不了解的，因为作者也没说这个在合并的时候，通过边就可以实现动态的修改parent数组，

因此我在修改的时候很好的理解，并做出了改进。

3.该代码我测试了，结果是正确的。如果有任何问题，希望你提醒我,谢谢！

*/