树的重心——树与图的深度优先遍历

问题描述

思路

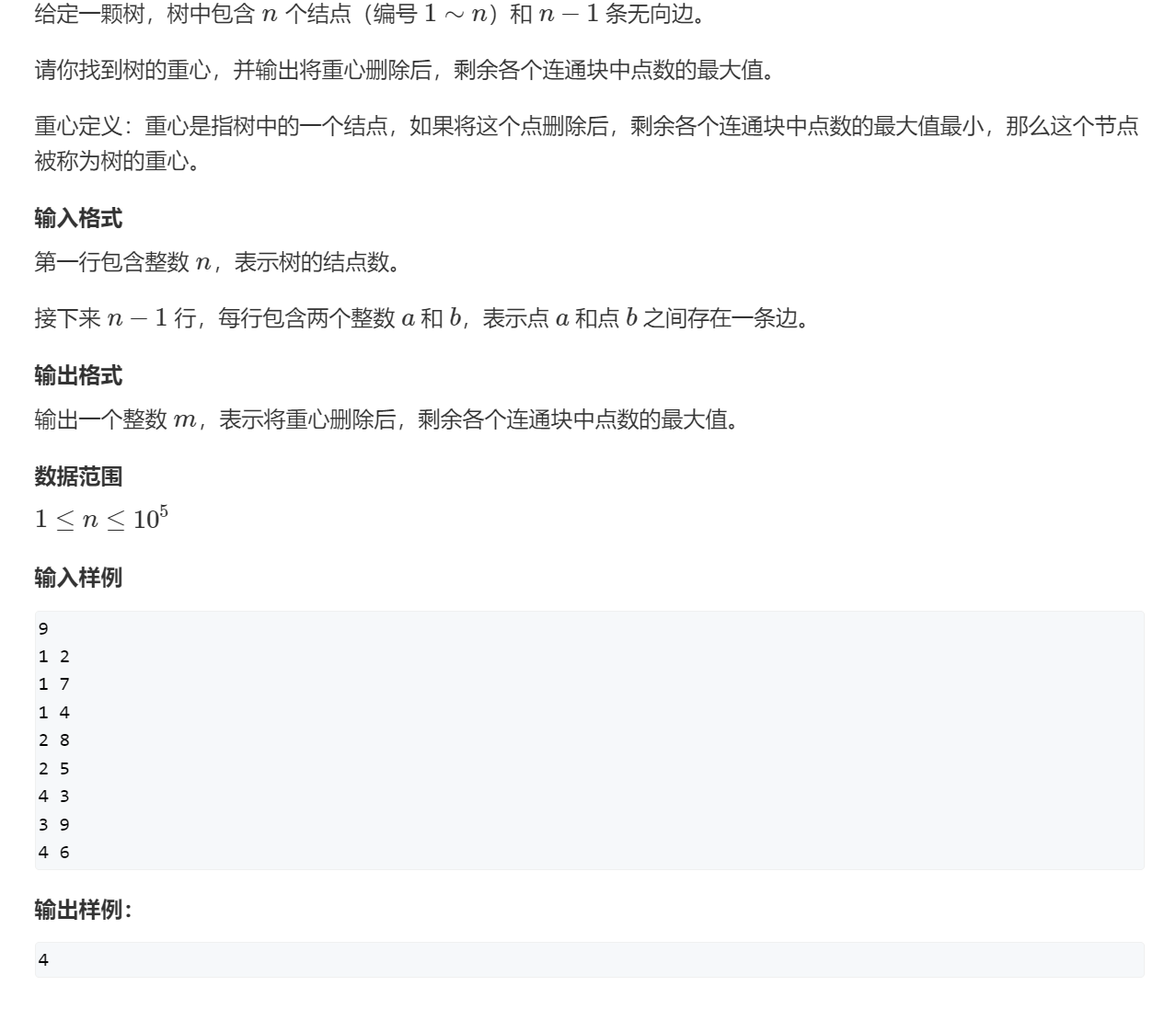
什么是连通块

• 如果把2这个节点删除后，可以得到三个连通块

1. 8：点数1
2. 5：点数1
3. 7、1、4、6、3、9：点数6

怎么求树的重心？

• 删除每一个节点，求出当前剩余连通块中点数的最大值，再比较出最大值中的最小值
• 从任意一个节点开始，进行深度优先搜索
• 每次递归记录以当前节点为根的时候，节点的个数
• 用n - 以当前节点为根的节点个数表示剩余一个连通块中节点的个数
• 比较删除当前节点之后，剩余连通块中的点数，找到最大值
• 从最大值中找出最小值

树怎么存储？

• 树是一种特殊的图，因此可以使用存储图的方法来存储树
• 使用邻接表存储树

// idx表示边的编号
// h[]中存储的是真实的节点指向的边的编号，
// e[]数组中存储的是边的编号对应的节点，
//ne[]数组存储的是边的编号指向的下一个边的编号
int h[N], e[N], ne[N], idx;

// a节点与b节点建立一条边
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

代码实现

#include <cstring> 
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int n;
int h[N], e[N * 2], ne[N * 2], idx;		// 邻接表存储图
int res = N;	// 删除重心后剩下连通块中的最大值
bool st[N];		// 当前节点是否被遍历过

void add(int a, int b)	// 邻接表存储图
{
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int dfs(int u)
{
	st[u] = true;	// 当前节点已经遍历
	int sum = 1, tem = 0;	// sum表示以u为根的子树的节点数量，tem表示删除u这个节点后，剩余连通块中点数的最大值
	for(int i = h[u]; i != -1; i = ne[i])	// 节点u指向的边
	{
	    int j = e[i];	// 与节点u相连的节点
		if(!st[j])	// 如果没有遍历过
		{
			int t = dfs(j);	// 以节点j为根的子树的节点数量，也是删除节点u之后的一个连通块
			tem = max(tem, t);	// 连通块点数比较，找出最大值
			sum += t;	// 将子树节点数量加入到节点u中
		}
		
	}
	tem = max(tem, n - sum);	// 还剩余一个连通块
	res = min(res, tem);	// 找出最大值中的最小值
	
	return sum;
}

int main()
{
	cin >> n;
    // 邻接表头指针初始化
	memset(h, -1, sizeof h);
	for(int i = 1; i < n ;i++)	// 无向图，插入a -> b、b -> a
	{
		int a, b;
		cin >> a >> b;
		add(a, b);
		add(b, a);
	}
	dfs(1);		// 从节点1开始深搜
	cout << res << endl;
	
	return 0;
}