代码随想录刷题题Day36

刷题的第三十六天，希望自己能够不断坚持下去，迎来蜕变。😀😀😀
刷题语言：C++
Day36 任务
● 123.买卖股票的最佳时机III
● 188.买卖股票的最佳时机IV

1 买卖股票的最佳时机III

123.买卖股票的最佳时机III

思路：
动态规划
关键在于至多买卖两次，这意味着可以买卖一次，可以买卖两次，也可以不买卖。
（1）确定dp数组以及下标的含义
一天一共就有五个状态

1. 没有操作
2. 第一次持有股票
3. 第一次不持有股票
4. 第二次持有股票
5. 第二次不持有股票

dp[i][j]：i表示第i天，j为 [0 - 4] 五个状态，dp[i][j]表示第i天状态j所剩最大现金。

（2）确定递推公式

达到dp[i][1]状态，有两个具体操作：

• 操作一：第i天买入股票了，那么dp[i][1] = dp[i-1][0] - prices[i]
• 操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]

$dp[i][1]=max(dp[i?1][0]?prices[i],dp[i?1][1]);$
$dp[i][2]=max(dp[i?1][1]+prices[i],dp[i?1][2])$
$dp[i][3]=max(dp[i?1][3],dp[i?1][2]?prices[i]);$
$dp[i][4]=max(dp[i?1][4],dp[i?1][3]+prices[i]);$
（3）dp数组如何初始化

dp[0][0] = 0;
dp[0][1] = -prices[0];
dp[0][2] = 0;
dp[0][3] = -prices[0];
dp[0][4] = 0;

（4）确定遍历顺序:从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值
（5）举例推导dp数组

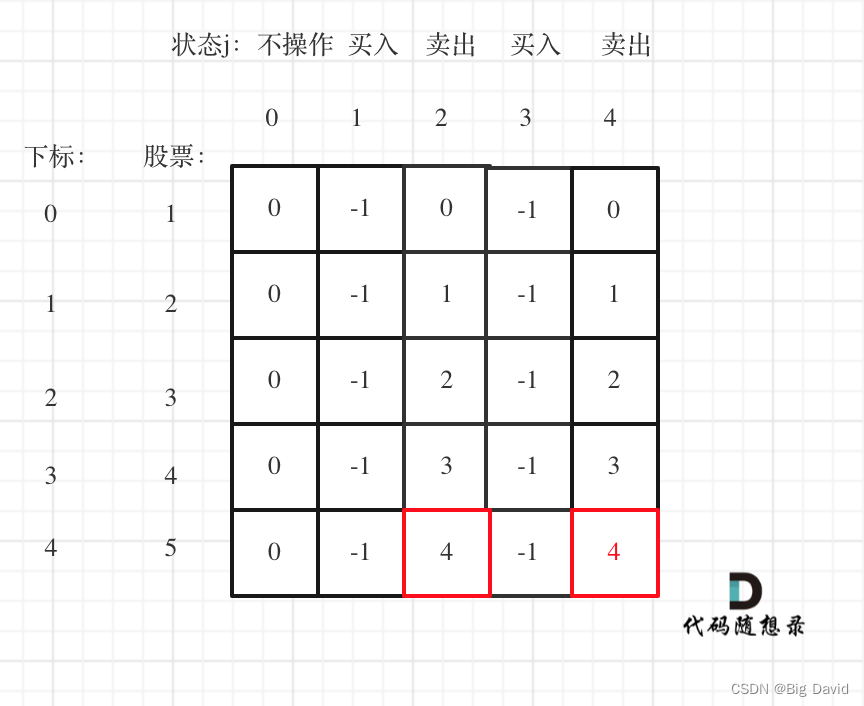
C++：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.size() == 0) return 0;
        vector<vector<int>> dp(prices.size(), vector<int>(5, 0));
        dp[0][1] = -prices[0];
        dp[0][3] = -prices[0];
        for (int i = 1; i < prices.size(); i++) {
            dp[i][0] = dp[i - 1][0];
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        return dp[prices.size() - 1][4];
    }
};

时间复杂度：$O(n)$
空间复杂度：$O(n\times 5)$

2 买卖股票的最佳时机IV

188.买卖股票的最佳时机IV

思路：
动态规划
（1）确定dp数组以及下标的含义
使用二维数组 dp[i][j] ：第i天的状态为j，所剩下的最大现金是dp[i][j]
j的状态表示为：

• 0 表示不操作
• 1 第一次买入
• 2 第一次卖出
• 3 第二次买入
• 4 第二次卖出
• …

除了0以外，偶数就是卖出，奇数就是买入。

vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0);

（2）确定递推公式

for (int j = 0; j < 2 * k - 1; j += 2) {
	dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
	dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}

（3）dp数组如何初始化

for (int j = 1; j < 2 * k; j++) {
	dp[0][j] = -prices[0];
}

（4）确定遍历顺序：从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值。
（5）举例推导dp数组

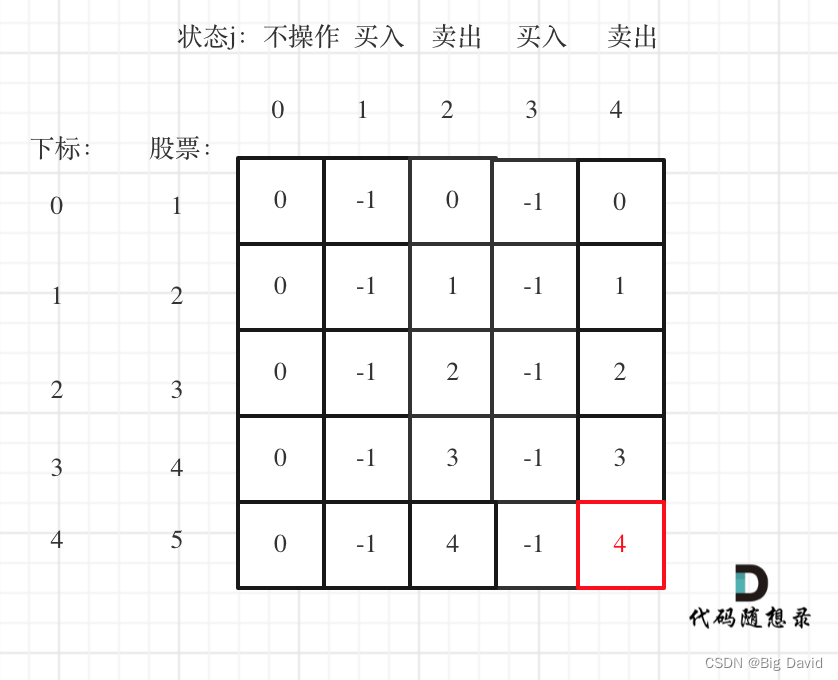
最后一次卖出，一定是利润最大的，dp[prices.size() - 1][2 * k]即红色部分就是最后求解。

C++：

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        if (prices.size() == 0) return 0;
        vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
        for (int j = 1; j < 2 * k; j += 2) {
            dp[0][j] = -prices[0];
        }
        for (int i = 1; i < prices.size(); i++) {
            for (int j = 0; j < 2 * k - 1; j += 2) {
                dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
                dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
            }
        }
        return dp[prices.size() - 1][2 * k];
    }
};

时间复杂度: $O(n?k)$，其中 n 为 prices 的长度
空间复杂度: $O(n?k)$

---

鼓励坚持三十七天的自己😀😀😀