统计学之常见的分布介绍

统计学中常见的分布有：

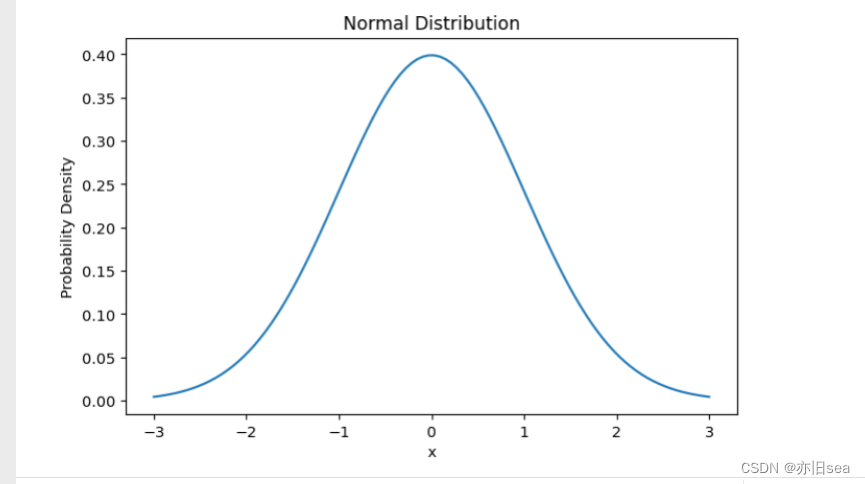
1. 正态分布（Normal Distribution）：也称为高斯分布，是最常见的分布之一，具有钟形曲线，对称且均值和标准差可以完全描述该分布。

2. 二项分布（Binomial Distribution）：描述了重复进行一系列独立的二元试验，例如抛硬币或进行有限次数的成功与失败的实验。它的特征是具有确定的成功概率和试验次数。

3. 泊松分布（Poisson Distribution）：适用于描述单位时间或空间内随机事件发生次数的概率分布。它主要用于计算罕见事件的概率，例如计算在某个时间段内发生的车祸的数量。

4. 均匀分布（Uniform Distribution）：以一致的概率分布在一定范围内随机地选择数值。在一个区间内的每个值都有相等的概率。

5. 指数分布（Exponential Distribution）：描述了时间或空间上连续事件的间隔时间。它经常用于建模随机事件的时间间隔。

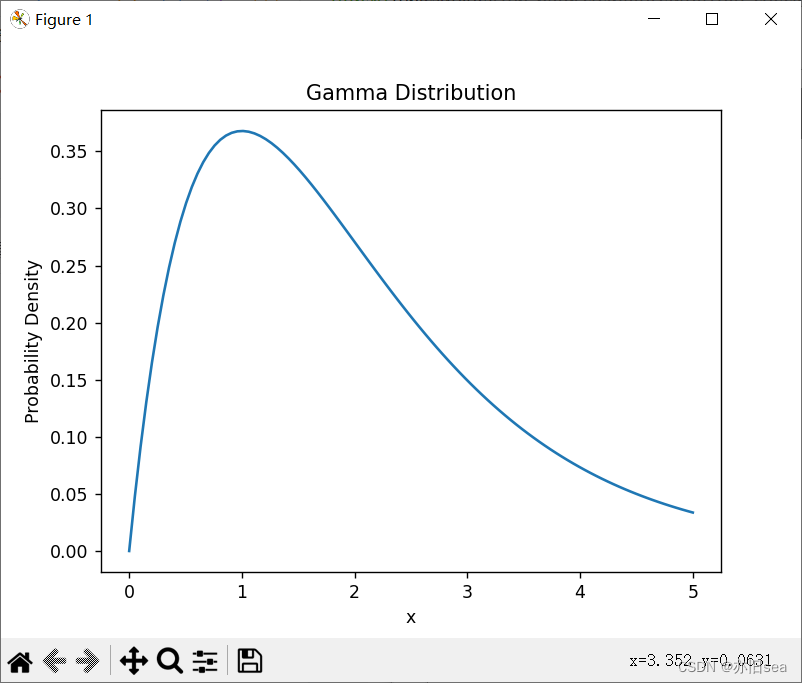
6. 伽马分布（Gamma Distribution）：是指数分布的推广，适用于描述连续时间事件的等候时间。

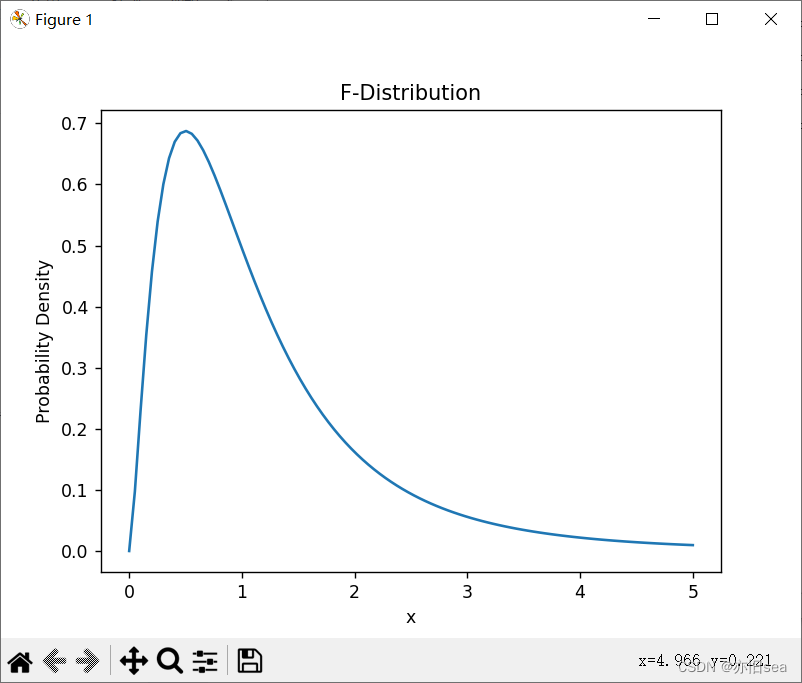
7. F分布（F-Distribution）：应用于统计假设检验，例如比较两个样本方差的差异。

8. t分布（t-Distribution）：常用于小样本量的假设检验，例如在小样本下进行均值的比较。

这只是一些统计学中常见的分布，实际上还有很多其他的分布，每个分布都有不同的应用和特点。

正态分布的特点是具有钟形曲线，对称且均值和标准差可以完全描述该分布。实际案例包括身高、体重、智商等连续数据的分布。

二项分布的特点是描述了重复进行一系列独立的二元试验，具有确定的成功概率和试验次数。实际案例包括抛硬币、掷骰子、进行有限次数的成功与失败的实验。

泊松分布的特点是适用于描述单位时间或空间内随机事件发生次数的概率分布。实际案例包括计算在某个时间段内发生的交通事故、电话呼叫、邮件到达等事件的数量。

均匀分布的特点是在一定范围内随机地选择数值，每个值都有相等的概率。实际案例包括抽奖活动、随机选择样本等。

指数分布的特点是描述了时间或空间上连续事件的间隔时间。实际案例包括计算连续时间内发生两次事件的间隔时间，例如两次用户登录网站的间隔时间。

伽马分布是指数分布的推广，适用于描述连续时间事件的等候时间。实际案例包括计算连续时间内多次事件的总等候时间，例如多次用户登录网站的总等候时间。

F分布主要应用于统计假设检验，例如比较两个样本方差的差异。实际案例包括在实验中比较两种不同处理的效果。

t分布常用于小样本量的假设检验，例如在小样本下进行均值的比较。实际案例包括小样本量的调查研究、实验设计中的差异检验。

以下是使用Python生成这几种分布的示例代码：

正态分布：

import numpy as np
import matplotlib.pyplot as plt

mean = 0
std = 1

data = np.random.normal(mean, std, 1000)
plt.hist(data, bins=30, density=True)
plt.show()

二项分布：

import numpy as np
import matplotlib.pyplot as plt

n = 10
p = 0.5

data = np.random.binomial(n, p, 1000)
plt.hist(data, bins=n+1, range=[0, n], density=True)
plt.show()

泊松分布：

import numpy as np
import matplotlib.pyplot as plt

lam = 3

data = np.random.poisson(lam, 1000)
plt.hist(data, bins=20, density=True)
plt.show()

均匀分布：

import numpy as np
import matplotlib.pyplot as plt

a = 0
b = 10

data = np.random.uniform(a, b, 1000)
plt.hist(data, bins=30, density=True)
plt.show()

指数分布：

import numpy as np
import matplotlib.pyplot as plt

lam = 0.5

data = np.random.exponential(1/lam, 1000)
plt.hist(data, bins=30, density=True)
plt.show()

伽马分布：

import numpy as np
import matplotlib.pyplot as plt

shape = 2
scale = 2

data = np.random.gamma(shape, scale, 1000)
plt.hist(data, bins=30, density=True)
plt.show()

F分布：

import numpy as np
import matplotlib.pyplot as plt

df1 = 5
df2 = 3

data = np.random.f(df1, df2, 1000)
plt.hist(data, bins=30, density=True)
plt.show()

t分布：

import numpy as np
import matplotlib.pyplot as plt

df = 10

data = np.random.standard_t(df, 1000)
plt.hist(data, bins=30, density=True)
plt.show()

以下是针对每种分布的一些常见检验的代码示例：

正态分布（Normal Distribution）：

1. Shapiro-Wilk正态性检验：

from scipy import stats

data = [1, 2, 3, 4, 5]  # 样本数据
stat, p = stats.shapiro(data)
alpha = 0.05  # 显著性水平

if p > alpha:
    print("样本数据符合正态分布")
else:
    print("样本数据不符合正态分布")

1. Anderson-Darling正态性检验：

from scipy import stats

data = [1, 2, 3, 4, 5]  # 样本数据
result = stats.anderson(data, dist='norm')
alpha = 0.05  # 显著性水平

if result.statistic < result.critical_values[2]:
    print("样本数据符合正态分布")
else:
    print("样本数据不符合正态分布")

二项分布（Binomial Distribution）：

1. 假设检验（使用二项分布的情况）：

from scipy import stats

successes = 10  # 成功次数
n_trials = 20  # 总试验次数
p = 0.5  # 成功概率

result = stats.binom_test(successes, n_trials, p)
alpha = 0.05  # 显著性水平

if result > alpha:
    print("样本数据符合二项分布")
else:
    print("样本数据不符合二项分布")

泊松分布（Poisson Distribution）：

1. Goodness-of-Fit拟合度检验（Kolmogorov-Smirnov检验）：

from scipy import stats

observed_values = [10, 15, 12, 8]  # 观测到的频数
expected_values = [8, 12, 10, 15]  # 预期的频数

result = stats.kstest(observed_values, "poisson", args=(expected_values,))
alpha = 0.05  # 显著性水平

if result.pvalue > alpha:
    print("样本数据符合泊松分布")
else:
    print("样本数据不符合泊松分布")

均匀分布（Uniform Distribution）：

1. 假设检验（Kuiper检验）：

from scipy import stats

data = [0.1, 0.3, 0.5, 0.7, 0.9]  # 样本数据
result = stats.kstest(data, 'uniform')
alpha = 0.05  # 显著性水平

if result.pvalue > alpha:
    print("样本数据符合均匀分布")
else:
    print("样本数据不符合均匀分布")

指数分布（Exponential Distribution）：

1. 假设检验（Kolmogorov-Smirnov检验）

from scipy import stats

data = [0.1, 0.3, 0.5, 0.7, 0.9]  # 样本数据
result = stats.kstest(data, 'expon')
alpha = 0.05  # 显著性水平

if result.pvalue > alpha:
    print("样本数据符合指数分布")
else:
    print("样本数据不符合指数分布")

伽马分布（Gamma Distribution）：

1. 假设检验（Kolmogorov-Smirnov检验）：

from scipy import stats

data = [0.1, 0.3, 0.5, 0.7, 0.9]  # 样本数据
result = stats.kstest(data, 'gamma', args=(1,))
alpha = 0.05  # 显著性水平

if result.pvalue > alpha:
    print("样本数据符合伽马分布")
else:
    print("样本数据不符合伽马分布")

F分布（F-Distribution）：

1. 方差比较（F检验）：

from scipy import stats

data1 = [1, 2, 3, 4, 5]  # 样本数据1
data2 = [2, 4, 6, 8, 10]  # 样本数据2

result = stats.f_oneway(data1, data2)
alpha = 0.05  # 显著性水平

if result.pvalue > alpha:
    print("样本数据的方差相等")
else:
    print("样本数据的方差不相等")

t分布（t-Distribution）：

1. 均值比较（单样本t检验）：

from scipy import stats

data = [1, 2, 3, 4, 5]  # 样本数据
result = stats.ttest_1samp(data, 0)
alpha = 0.05  # 显著性水平

if result.pvalue > alpha:
    print("样本数据的均值为0")
else:
    print("样本数据的均值不为0")

这些代码示例只是简单的演示了如何使用Python中的SciPy库进行一些基本的分布检验。请注意，在实际应用中，需要根据具体的问题和数据类型选择适当的检验方法和参数设置，并根据需要进行进一步的数据处理和解释。

以下是使用Python绘制几种常见分布的密度曲线图的示例代码：

1. 正态分布（Normal Distribution）：

```python
import numpy as np
import matplotlib.pyplot as plt

mu = 0 # 均值
sigma = 1 # 标准差

x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)
y = (1/(sigma * np.sqrt(2*np.pi))) * np.exp(-0.5*((x-mu)/sigma)**2)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('Normal Distribution')
plt.show()
```

2. 二项分布（Binomial Distribution）：

```python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom

n = 10 # 试验次数
p = 0.5 # 成功概率

x = np.arange(0, n+1)
y = binom.pmf(x, n, p)

plt.stem(x, y)
plt.xlabel('x')
plt.ylabel('Probability Mass')
plt.title('Binomial Distribution')
plt.show()
```

3. 泊松分布（Poisson Distribution）：

```python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson

lambda_ = 3 # 平均发生率

x = np.arange(0, 10)
y = poisson.pmf(x, lambda_)

plt.stem(x, y)
plt.xlabel('x')
plt.ylabel('Probability Mass')
plt.title('Poisson Distribution')
plt.show()
```

4. 均匀分布（Uniform Distribution）：

```python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform

a = 0 # 范围起点
b = 1 # 范围终点

x = np.linspace(a, b, 100)
y = uniform.pdf(x, a, b-a)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('Uniform Distribution')
plt.show()
```

5. 指数分布（Exponential Distribution）：

```python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon

lambda_ = 1 # 指数分布参数

x = np.linspace(0, 5, 100)
y = expon.pdf(x, scale=1/lambda_)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('Exponential Distribution')
plt.show()
```

6. 伽马分布（Gamma Distribution）：

```python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma

alpha = 2 # 形状参数
beta = 1 # 尺度参数

x = np.linspace(0, 5, 100)
y = gamma.pdf(x, alpha, scale=1/beta)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('Gamma Distribution')
plt.show()
```

7. F分布（F-Distribution）：

```python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import f

dfn = 5 # 分子自由度
dfd = 10 # 分母自由度

x = np.linspace(0, 5, 100)
y = f.pdf(x, dfn, dfd)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('F-Distribution')
plt.show()
```

8. t分布（t-Distribution）：

```python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t

df = 5 # 自由度

x = np.linspace(-5, 5, 100)
y = t.pdf(x, df)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('t-Distribution')
plt.show()
```

以上代码使用了SciPy库中相应分布的概率密度函数（pdf）绘制曲线图，并使用Matplotlib库进行可视化。根据需要，可以调整参数和绘图范围来适应不同的情况。