TP-GMM
Task-parameterized Gaussian mixture model (TP-GMM)
对于一组示教数据
ξ
∈
R
D
×
N
\bm{ξ} ∈R^{D×N}
ξ∈RD×N，从不同的坐标系去观测它
X
t
(
j
)
=
A
t
,
j
?
1
(
ξ
t
?
b
t
,
j
)
X^{(j)}_t=\bm{A}^{-1}_{t,j}(\bm{ξ}_t-\bm{b}_{t,j})
Xt(j)?=At,j?1?(ξt??bt,j?)
上标
j
j
j 代表坐标系，下标
t
t
t 代表 示教轨迹数据
(
d
a
t
a
p
o
i
n
t
s
)
(datapoints)
(datapoints)的索引，
A
A
A 和
b
b
b 代表坐标系
j
j
j的姿态描述和位置描述
TP-GMM 形式为有
K
K
K个
c
o
m
p
o
n
e
n
t
component
component 其形式为
{
π
i
,
{
μ
i
j
,
Σ
i
(
j
)
}
j
=
1
P
}
i
=
1
K
\{{\pi_i,\{μ_i^{j},Σ^{(j)}_i}\}^P_{j=1}\}^K_{i=1}
{πi?,{μij?,Σi(j)?}j=1P?}i=1K?
可以看出均值
μ
{μ}
μ 和
Σ
Σ
Σ 方差 的维度为
K
×
P
K×P
K×P
直接拿不同坐标系数据去训练, 扩张维度, 是不是太生猛一点了
训练完后需要去掉坐标系维度,得到最终的 TP-GMM。论文的做法是，对于每个
c
o
m
p
o
n
e
n
t
component
component 存在
P
P
P 个分布，将这
P
P
P 个高斯分布相乘，最终得到的结果是：
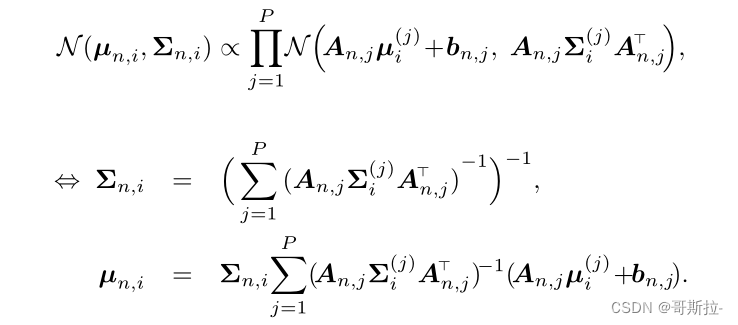
得到最终
T
P
?
G
M
M
TP-GMM
TP?GMM 后进行高斯混合回归，对于任务空间中的轨迹数据，上标 I 对应于时间输入维度，O 对应于描述任务空间中路径(位置和方向)的输出维度。n 代表迭代次数，
ξ
n
I
ξ_n^I
ξnI? 和
ξ
n
o
ξ_n^o
ξno? 代表输入和输出。训练出的TP-GMM模型是输入输出的联合分布，将 TP-GMM 的均值和方差拆成输入输出两部分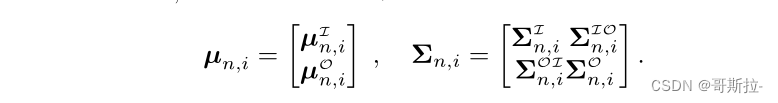
GMR依赖该联合分布
P
(
ξ
n
I
,
ξ
n
o
)
P(ξ_n^I, ξ_n^o )
P(ξnI?,ξno?) 估计条件概率
P
(
ξ
n
I
∣
ξ
n
o
)
P(ξ_n^I | ξ_n^o )
P(ξnI?∣ξno?) ，最终的分布为
N
(
ξ
^
n
O
,
Σ
^
n
O
)
N (\hat ξ^O_n, \hatΣ^O_n)
N(ξ^?nO?,Σ^nO?)
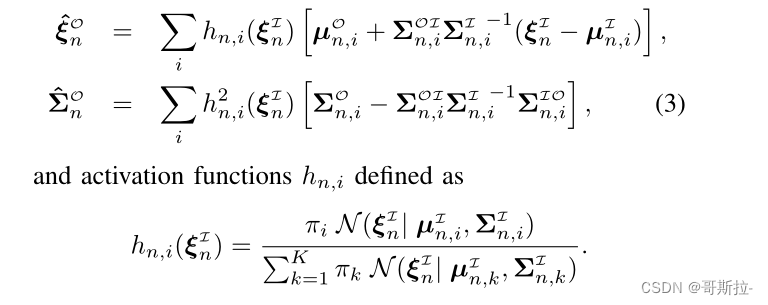
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！