二叉树的创建与遍历

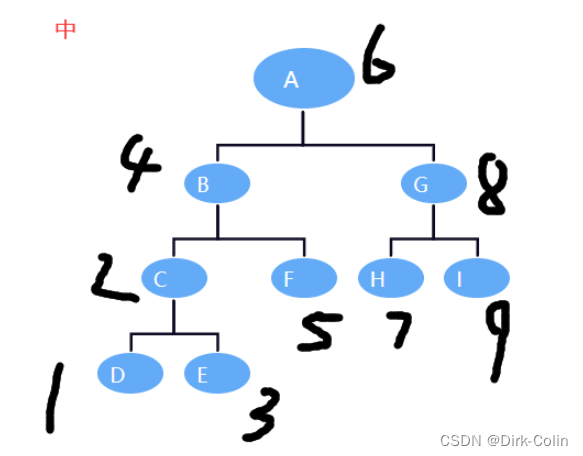
对于前序遍历，首先访问当前节点，然后递归地遍历左子树和右子树。
这就是为什么前序遍历的代码中，首先是 printf("%d ", root->data);。

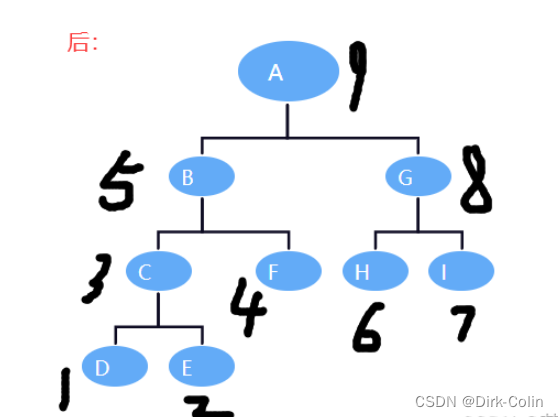
中序遍历：
对于中序遍历，首先递归地遍历左子树，然后访问当前节点，最后递归地遍历右子树。
这就是为什么中序遍历的代码中，左子树递归调用在当前节点访问之前，右子树递归调用在当前节点访问之后。

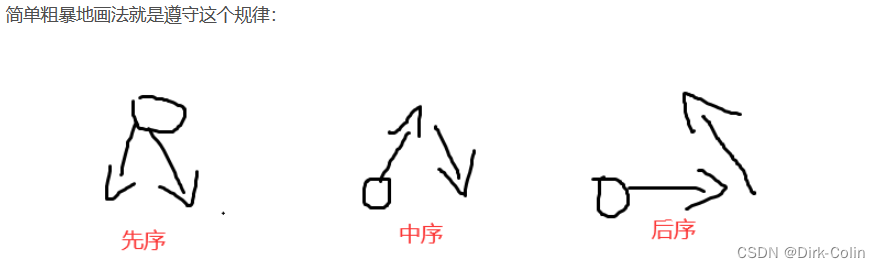
后序遍历：
对于后序遍历，首先递归地遍历左子树和右子树，最后访问当前节点。
这就是为什么后序遍历的代码中，左子树递归调用在当前节点访问之前，右子树递归调用在当前节点访问之前。

void preOrderTraversal(struct TreeNode* root) {
    if (root != NULL) {
        printf("%d ", root->data); // 访问当前节点
        preOrderTraversal(root->left); // 递归遍历左子树
        preOrderTraversal(root->right); // 递归遍历右子树
    }
}

?

?

// 中序遍历
void inOrderTraversal(struct TreeNode* root) {
    if (root != NULL) {
        inOrderTraversal(root->left); // 递归遍历左子树
        printf("%d ", root->data); // 访问当前节点
        inOrderTraversal(root->right); // 递归遍历右子树
    }
}

?

?

void postOrderTraversal(struct TreeNode* root) {
    if (root != NULL) {
        postOrderTraversal(root->left); // 递归遍历左子树
        postOrderTraversal(root->right); // 递归遍历右子树
        printf("%d ", root->data); // 访问当前节点
    }
}

二叉树的创建：

// 定义二叉树结构
struct TreeNode {
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
};

// 创建新的二叉树节点
struct TreeNode* createNode(int value) {
    struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    newNode->data = value;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

?测试代码：

int main() {
    // 构建一个简单的二叉树
    struct TreeNode* root = createNode(1);
    root->left = createNode(2);
    root->right = createNode(3);
    root->left->left = createNode(4);
    root->left->right = createNode(5);

    // 前序遍历
    printf("前序遍历: ");
    preOrderTraversal(root);
    printf("\n");

    // 中序遍历
    printf("中序遍历: ");
    inOrderTraversal(root);
    printf("\n");

    // 后序遍历
    printf("后序遍历: ");
    postOrderTraversal(root);
    printf("\n");

    return 0;
}