位运算 (运算符)
文章目录
位运算
位运算概述
从现代计算机中所有的数据二进制的形式存储在设备中。即 0、1 两种状态,计算机对二进制数据进行的运算(+、-、*、/)都是叫位运算,即将符号位共同参与运算的运算。
let a = 30;
let b = 43;
let c = a + b;
计算两个数的和,因为在计算机中都是以二进制来进行运算,所以上面我们所给的 let 变量会在机器内部先转换为二进制在进行相加:
30: 0 0 0 1 1 1 1 0
43: 0 0 1 0 1 0 1 1
————————————————————
73: 0 1 0 0 1 0 0 1
相比在代码中直接使用(+、-、*、/)运算符,合理的运用位运算更能显著提高代码在机器上的执行效率。
位运算概览
| 符号 | 描述 | 运算规则 |
|---|---|---|
| & | 与 | 两个位都为1时,结果才为1 |
| | | 或 | 两个位都为0时,结果才为0 |
| ^ | 异或 | 两个位相同为0,相异为1 |
| ~ | 取反 | 0变1,1变0 |
| << | 左移 | 各二进位全部左移若干位,高位丢弃,低位补0 |
| >> | 右移 | 各二进位全部右移若干位,对无符号数,高位补0,有符号数,各编译器处理方法不一样,有的补符号位(算术右移),有的补0(逻辑右移) |
& 按位与(AND)
- 按位与操作通常用于掩码操作,即用来屏蔽某些位或者检验某些位是否设置。
// 示例 1: // 5: 00000101 // 10: 00001010 // &运算: 00000000 console.log(5 & 10); // 结果是 0
| 按位或(bitwise OR)
- 按位或操作常用于设置(将位设置为1)或合并位标志。
// 示例 1: // 5: 00000101 // 10: 00001010 // |运算: 00001111 console.log(5 | 10); // 结果是 15
^ 按位异或(bitwise XOR)
- 按位异或操作常用于切换位的状态,或者在不使用中间变量的情况下交换两个变量的值。
// 示例 1: // 5: 00000101 // 10: 00001010 // ^运算: 00001111 console.log(5 ^ 10); // 结果是 15
~ 按位非(bitwise NOT)
- 在 JavaScript 中,整数使用补码形式存储。对于按位非操作,其效果可以认为是对操作数加1然后变为相反数(负数),或者可以理解为对操作数的相反数减1
// 示例 1: console.log(~5); // 5 的二进制是 0000 0101,取反得到 1111 1010,这是 -6 的补码表示 // 示例 2: console.log(~-1); // -1 的二进制是 1111 1111(所有位都是1),取反得到 0000 0000,这是 0
<< 左移(bitwise shift left)
-
左移操作可以被视为对一个数进行乘法运算,具体地说,将一个数左移n位相当于将这个数乘以2的n次方(2^n)。
// 示例 1: // 1: 00000001 (二进制) // 1 << 2: 00000100 (二进制) console.log(1 << 2); // 结果是 4 (十进制) //对于 1 << 2,数 1 的二进制表示 00000001 被左移了2位,变成了 00000100,这是 4 的二进制表示。
>> 带符号右移(signed right shift)
- 带符号右移操作可以看作是对一个数进行除法运算,具体地说,将一个数右移 n 位相当于将这个数除以 2 的 n 次方(2^n),并且结果向下取整(对于负数来说就是远离零方向取整)。
// 示例 1: // 4: 00000100 (二进制) // 4 >> 1: 00000010 (二进制) console.log(4 >> 1); // 结果是 2 (十进制) // 示例 2: // -8: 11111000 (二进制的补码表示) // -8 >> 2: 11111110 (二进制的补码表示) console.log(-8 >> 2); // 结果是 -2 (十进制) 在上面的例子中: 对于 4 >> 1,数 4 的二进制表示 00000100 被右移了 1 位,变成了 00000010,这是 2 的二进制表示。 对于 -8 >> 2,数 -8 的二进制补码表示(假定是 8 位)是 11111000,右移 2 位后变成了 11111110,这是 -2 的二进制补码表示。
复合赋值运算符
&= 例:a&=b 相当于 a=a&b
|= 例:a|=b 相当于 a=a|b
>>= 例:a>>=b 相当于 a=a>>b
<<= 例:a<<=b 相当于 a=a<<b
^= 例:a^=b 相当于 a=a^b
Number 编码
JavaScript 的 Number 类型是一个双精度 64 位二进制格式 IEEE 754 值,类似于 Java 或者 C# 中的 double。这意味着它可以表示小数值,但是存储的数字的大小和精度有一些限制。简而言之,IEEE 754 双精度浮点数使用 64 位来表示 3 个部分:
1 位用于表示符号(sign)(正数或者负数)
11 位用于表示指数(exponent)(-1022 到 1023)
52 位用于表示尾数(mantissa)(表示 0 和 1 之间的数值)
尾数(也称为有效数)是表示实际值(有效数字)的数值部分。指数是尾数应乘以的 2 的幂次。将其视为科学计数法:
二进制运算符
- 二进制运算符将它们的操作数作为 32 个二进制位(0 或 1)的集合,并返回标准的 JavaScript 数值。
- 由于 JavaScript 中的数字是以 IEEE 754 双精度浮点格式存储的,但位运算符会将其操作数转换为32位有符号整数进行操作。因此,结果也是一个32位整数。还需要考虑的是,如果左移操作会导致数值超出32位整数的表示范围,那么结果将会被截断以适应32位整数的范围。
JavaScript Number 编码
- JavaScript 的 Number 类型是一个双精度 64 位二进制格式 IEEE 754 值,类似于 Java 或者 C# 中的 double。这意味着它可以表示小数值,但是存储的数字的大小和精度有一些限制。简而言之,IEEE 754 双精度浮点数使用 64 位来表示 3 个部分:
- 1 位用于表示符号(sign)(正数或者负数)
- 11 位用于表示指数(exponent)(-1022 到 1023)
- 52 位用于表示尾数(mantissa)(表示 0 和 1 之间的数值)
- 尾数(也称为有效数)是表示实际值(有效数字)的数值部分。指数是尾数应乘以的 2 的幂次。将其视为科学计数法:
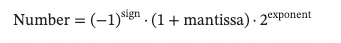
- 尾数使用 52 比特存储,在二进制小数中解释为 1.… 之后的数字。因此,尾数的精度是 2-52(可以通过 Number.EPSILON 获得),或者十进制数小数点后大约 15 到 17 位;超过这个精度的算术会受到舍入的影响。
- 一个数值可以容纳的最大值是 21024 - 1(指数为 1023,尾数为基于二进制的 0.1111…),可以通过 Number.MAX_VALUE 获得。超过这个值的数会被替换为特殊的数值常量 Infinity。
只有在 -253 + 1 到 253 - 1 范围内(闭区间)的整数才能在不丢失精度的情况下被表示(可通过 Number.MIN_SAFE_INTEGER 和 Number.MAX_SAFE_INTEGER 获得),因为尾数只能容纳 53 位(包括前导 1)。
有关这部份的更多详细信息,请参阅 ECMAScript 标准。
补码
在计算机系统中,整数通常以补码(two’s complement)形式存储。补码是一种特殊的二进制表示方法,用于编码有符号整数。在补码系统中,正数和0的表示与常规二进制相同,但负数的表示则不同。补码使得加法和减法的运算可以统一处理,简化了计算机的硬件实现。
我们需要了解如何从一个正数的二进制表示得到其负数的补码表示。以下是将正数转换为其负数补码表示的步骤:
写出正数的二进制表示。假设我们要找的是 6 的补码表示。6 的二进制表示(8位表示)是 0000 0110。
对这个二进制数取反(位反)。将所有的 0 变成 1,所有的 1 变成 0。所以 0000 0110 取反后变为 1111 1001。
给取反后的结果加上 1。在我们的例子中,1111 1001 加上 1 结果是 1111 1010。
这个得到的结果 1111 1010 就是 -6 的补码表示。在补码系统中,最左边的位是符号位:0 表示正数,1 表示负数。所以当我们看到 1111 1010 这样的二进制数,最左边的 1 告诉我们这是一个负数。
现在来验证这个结果。为了将补码转换回十进制,我们可以进行以下步骤:
因为符号位是 1,我们知道这是一个负数的补码表示。
我们取它的相反数,即再次取反并加 1。1111 1010 取反得到 0000 0101,加 1 得到 0000 0110。
我们将 0000 0110 转换回十进制,结果是 6。因为我们开始的是一个负数的补码,所以原来的数是 -6。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!