第三十五周:文献阅读+Self-attention
目录
摘要
本周阅读的文献提出了AT-LSTM模型即注意力机制结合LSTM模型,用于提高水质检测的精确度。AT-LSTM模型与传统LSTM模型相比的不同之处在于增加了注意力层,通过对神经网络隐含层元素进行自适应加权,减少无关因素对结果的影响,突出相关因素的影响,从而提高预测精度。研究通过与单一模型的对比实验,验证了借助注意力机制的AT-LSTM模型在多元时间序列的预测性的优势。self-attention是一种可以考虑全局信息以及不同输入向量之间关系的机制,在训练时可以充分发挥这些关系,优化训练的结果。通过计算输入之间的关联性,过滤掉无效的信息,减少计算量。
Abstract
The literature read this week proposes the AT-LSTM model, which combines attention mechanism with LSTM model, to improve the accuracy of water quality detection. The difference between the AT-LSTM model and the traditional LSTM model lies in the addition of an attention layer. By adaptively weighting the hidden layer elements of the neural network, the influence of irrelevant factors on the results is reduced, and the influence of related factors is highlighted, thereby improving prediction accuracy. The study verified the predictive advantage of AT-LSTM model in multivariate time series by comparing it with a single model. Self attention is a mechanism that considers global information and the relationships between different input vectors, which can be fully utilized during training to optimize the training results. By calculating the correlation between inputs, filtering out invalid information and reducing computational complexity.
文献阅读:基于LSTM和注意机制的水质预测
title:Water Quality Prediction Based on LSTM and Attention Mechanism: A Case Study of the Burnett River, Australia
现有问题
1)水质指标种类繁多、水质数据采集周期长、水质指标间相关性强、水质特征非线性、数据波动性大等特点,准确有效地预测水质已成为一个具有挑战性的问题。河流水质在宏观时间尺度上表现出季节性和周期性等特征,具有非线性和不确定性。
2)大多数水质数据属于长相关序列数据,在相应的时间序列中可能存在一些延迟和间隔较长的重要事件。结合LSTM和卷积神经网络(CNN)的混合模型,在预测水质变量方面,其性能优于单一机器学习模型,但LSTM缺乏对子窗口特征进行不同程度关注的能力,这可能会导致一些相关信息被忽略,无法重视时间序列的重要特征。
提出方法
1)开发长短期记忆(LSTM)网络及其基于注意力的(AT-LSTM)模型,对伯内特河断面水质数据进行特征提取后,考虑不同时刻序列对预测结果的影响,引入注意力机制,增强关键特征对预测结果的影响。
2)分别利用 LSTM 和 AT-LSTM 模型对伯内特河的溶解氧(DO)进行一步前向预测和多步前向预测,并对结果进行比较,判断注意力机制的加入是否提高了 LSTM 模型的预测性能。
前提点
1. LSTM
LSTM网络适合处理和预测时间序列中间隔和延迟非常长的时间序列特征。 LSTM网络还可以有效解决传统循环神经网络中容易出现的梯度消失和梯度爆炸问题。 LSTM模型有一个输入门、一个输出门和一个遗忘门,用于修改记忆。输入门和输出门主要用来控制输入特征和输出内容,而遗忘门主要用来决定记忆单元中哪些记忆应该保留,哪些记忆可以忘记。 LSTM的结构如图所示。
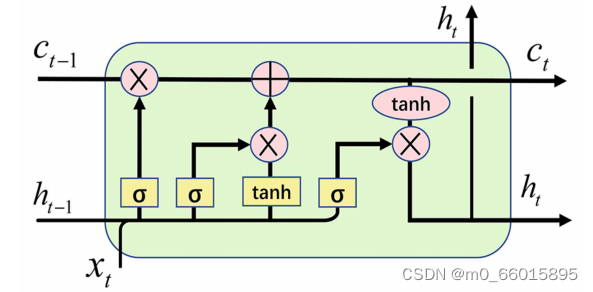
W矩阵表示各种门和记忆单元的参数矩阵,x表示输入值,h表示隐藏状态变量,主要用于存储和更新历史信息,σ和tan h表示sigmoid激活函数tan h 激活函数。一旦经过充分训练,LSTM 模型就可以提取复杂时间序列信息的特征。基于这些有效特征(来自 LSTM 模型的隐藏层信息),最终的全连接层能够将它们解码为具有合理精度的预测值。
2. 注意力机制
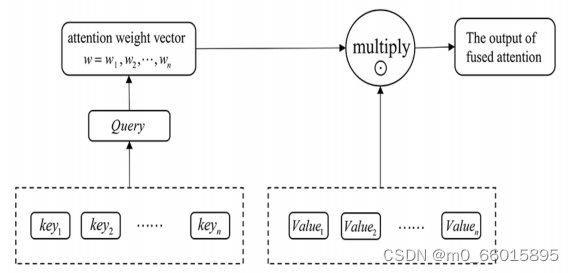
注意力机制的本质是,对于给定的目标,生成一个权重系数并与输入相乘,以识别输入中哪些特征对目标重要,哪些特征不重要。为了实现注意力机制,我们将输入的原始数据视为?key,value?对,并计算Key和Query之间的相似系数。根据目标中给定任务中的查询,我们可以得到 Value 对应的权重系数,然后将权重系数与 Value 相乘得到输出。我们使用 Q、K 和 V 来表示查询、键和值,计算权重系数W的公式为:
使用公式(1)将注意力权重系数W乘以值,得到包含注意力的输出a。
正如我们所看到的,注意力机制通过计算?key,value?形成注意力权重向量,然后乘以值以获得包含注意力的新输出。
Attention的计算分为三步:
- 计算Query和key之间的相似度,得到权重,常见的相似度函数有点积、拼接、感知器;
- 使用 softmax函数对这些权重进行归一化;
- 将权重与对应的key值相乘,得到最终的attention。
注意力机制在深度学习的各个领域都有很多应用。但需要注意的是,注意力并不是一个统一的模型,而只是一种在不同应用领域具有不同来源的 Query、key 和 value 的机制。这意味着不同的领域有不同的实现方法,因此可以结合不同的问题与其他模型结合得到更好的表现。
研究模型(AT-LSTM)结构
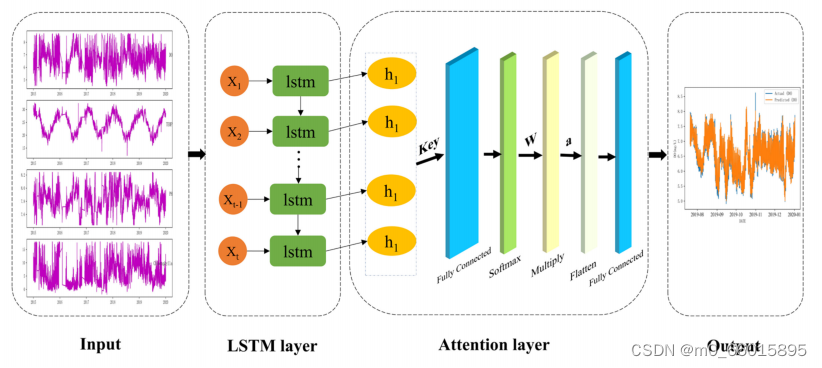
该模型的主要思想是通过对神经网络隐含层元素进行自适应加权,减少无关因素对结果的影响,突出相关因素的影响,从而提高预测精度。主要组成部分是LSTM层和注意力层,模型框架图如下图所示。将全连接层的输出通过softmax激活函数得到归一化的相似度权重。权重与输入层相乘来计算最终的注意力。扁平化层用于将输入“扁平化”,即将多维输入变成一维输入。模型的超参数设置在一定程度上影响其水质预测的性能。
AT-LSTM模型与传统LSTM模型相比的不同之处在于增加了注意力层,而其他主要结构相同。此外,模型是在相同的超参数下训练的,这有助于我们比较模型。根据上述原理,模型在过去的拟合结果的基础上进行学习,利用LSTM带记忆的特性来优化水质预测,最后通过全连接层激活后输出。
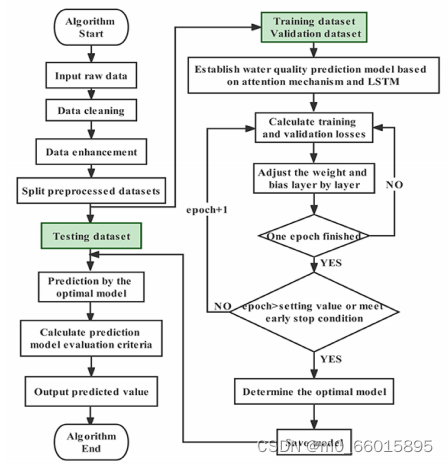
综合水质数据预测算法的具体过程如下:
步骤1:数据清洗。在进行水质预测之前,采用箱线图技术检测水质数据的异常值,并将异常值设置为空值,然后使用线性插值方法对空位值进行补充。
步骤2:数据增强。首先利用Pearson相关检验选择特征,进行不同水质参数之间的相关性分析,将与待预测特征相关的关键特征作为模型输入。其次采用滑动窗口技术,窗口大小为100来捕捉水质变量的趋势。最后使用最小-最大归一化来缓解不同特征尺度对模型训练的影响。
步骤3:训练模型。将水质数据按照8:1:1的比例分为三个数据集、训练集、验证集和测试集。在本研究中,训练集包含31802个小时条目(从2015年1月1日到2019年2月4日),验证集包含3975个小时条目(从2019年2月4日到2019年7月20日),测试集包含3975个小时条目(从2019年7月20日到2020年1月1日)。使用训练集来拟合数据样本,验证集来调整超参数,测试集来评估模型的预测性能和泛化能力。水质数据综合预测算法的具体流程如下:
模型验证
采用平均绝对误差(MAE)、均方根误差(RMSE)和决定系数(R2)定量评价模型预测效果。如果RMSE等于10,则可以认为回归效果与实际值的平均值相差10,其取值范围为0到正无穷,当它等于0时,表示模型是完美的,误差越大,表示误差值越大。R2表示模型的拟合能力,值越接近1,表示拟合能力越强。
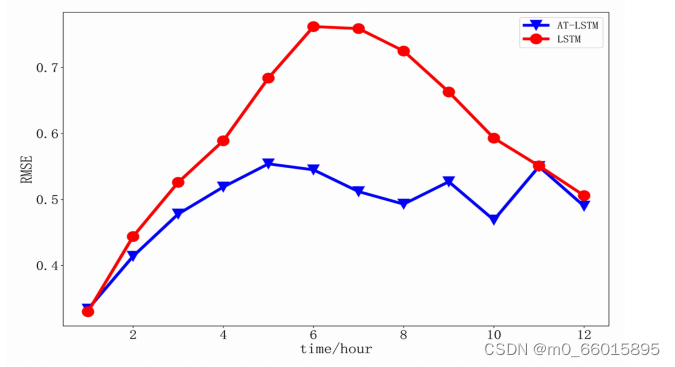
利用一个新的独立数据集(Gregory River数据)验证了AT-LSTM相对于LSTM在多元时间序列预测性能上的优势。在新数据集上使用LSTM模型和AT-LSTM模型提前1-12小时预测的RMSE对比如图所示。通过对比LSTM和AT-LSTM模型的RMSE与步骤的变化可以看出,AT-LSTM在新数据集上提前1-12 h预测的RMSE始终低于LSTM。这验证了本文提出的AT-LSTM模型在多元时间序列的预测性能上比传统的LSTM模型更具优势。
总结AT-LSTM优于LSTM的方面
- AT-LSTM比LSTM模型预测更加准确。因为注意力机制根据隐藏相关特征的不同重要性级别,为神经网络的隐含层元素分配相应的权重。因此,在LSTM模型相同的参数下,AT-LSTM模型可以更好地拟合DO的真实值,减小预测误差,提高模型的准确性。
- AT-LSTM模型比LSTM模型表现出更好的预测和更强的泛化能力。
- AT-LSTM模型在多元时间序列的预测性能上比传统LSTM模型更具优势,这再次说明注意力机制可以提高 AT-LSTM 模型在多元时间序列预测中的有效性和准确性
因此,通过研究,可以证明在水质预测方面,基于 AT-LSTM 的模型比单一的LSTM模型具有更强的能力,也就是借助注意力机制的AT-LSTM模型在多元时间序列的预测性能上比传统LSTM模型更具优势,可以为澳大利亚昆士兰州水质改善计划提供准确预测伯内特河水质的能力。?
Self-attention(自注意力机制)
1. 运作
Self-attention的输入通常是一串向量,而这个向量可能是这一整个神经网络的输入,也可能是某个隐藏层的输出。每个b都是考虑所有的a产生的。
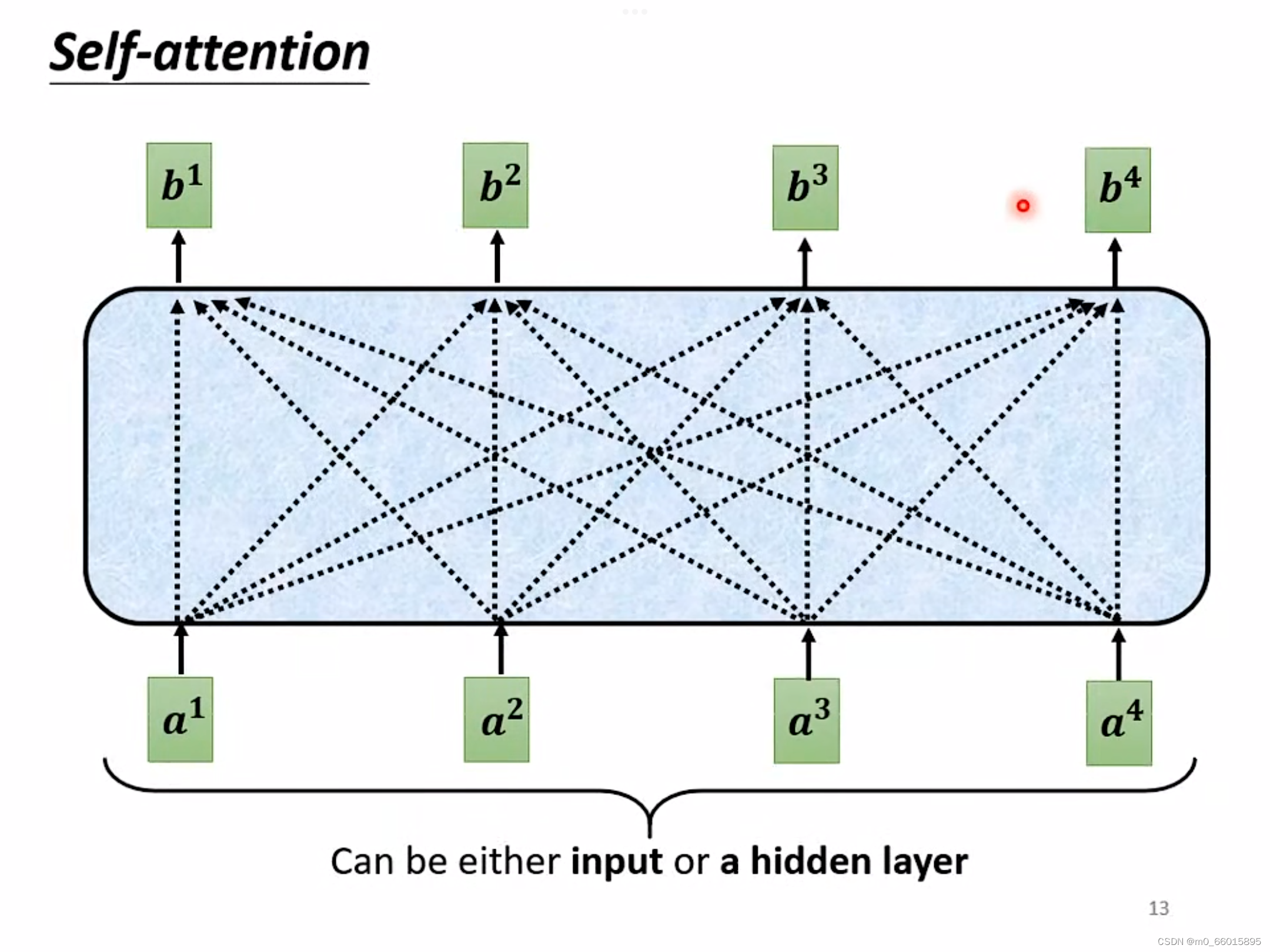
那么b是如何计算出来的?
以计算为例,首先根据
找出整个sequence里面跟
相关的其他向量,计算整个sequence里面所有向量跟向量
的关联度
,因为Self-attention就是为了考虑整个sequence,但又不希望把所有的信息都包括在window里面,所以需要找出哪些部分是重要的,因此通过这个机制过滤掉不重要的信息。
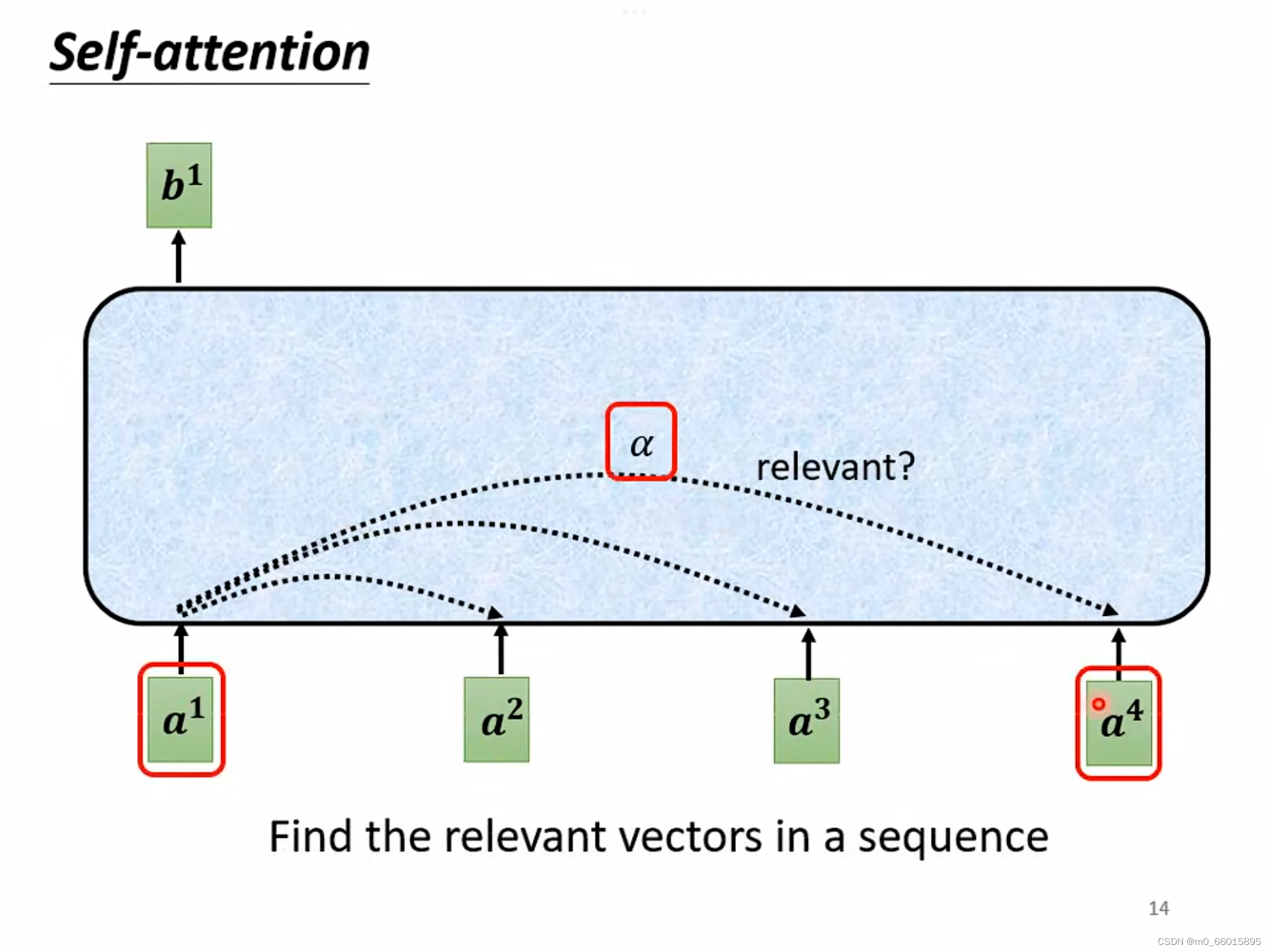
那么self-attention怎么找出每一个a呢?
方法一:Dot-product方法
将输入的两个向量分别乘以两个不同的矩阵
、
,得到向量q和一个数值k,最后q和k进行一个dot-product得到相关联度
。?
方法二:Additive
同样将输入的向量与两个矩阵相乘得到的向量相加,然后使用tanh投射到一个新的函数空间,再相乘得到最后结果。·
对每个输入的向量,两两之间按上面的方法计算出关联度,在得到关联度之后,将结果进行soft-max(也可以使用Relu等方法)计算出一个attention distribution,在得到attention distribution之后相比较就知道哪些向量与
关系密切,就可以根据
抽取出这个sequence里面重要的信息。
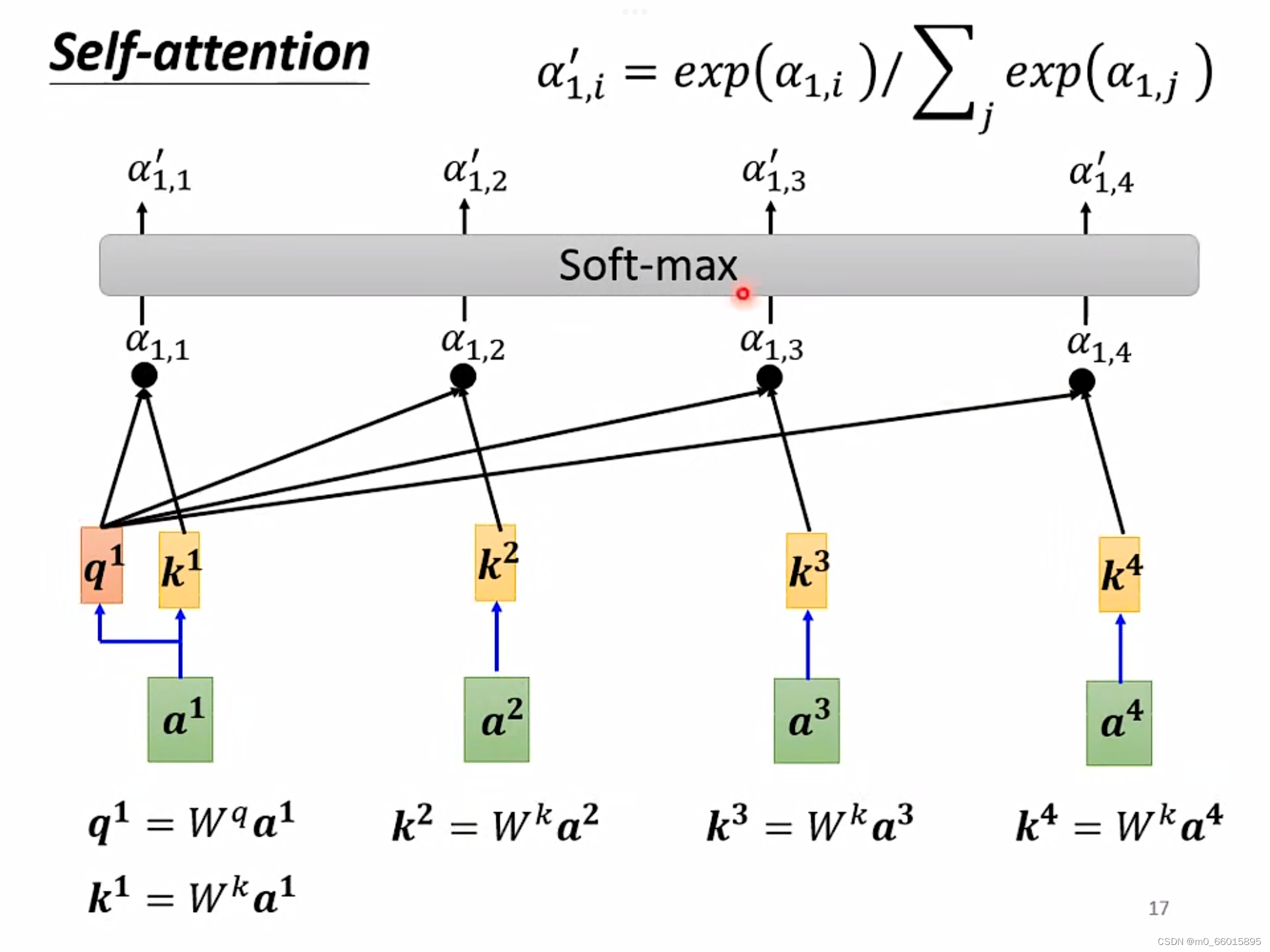
在得到每一个向量和之间的关联度之后,使用新的矩阵
乘上输入的向量
,得到一个新的矩阵
,然后将得到的关联度与矩阵
相乘,对每个输入的向量进行该操作,最后将每个关联度与矩阵
相乘的结果相加得到一个唯一数值
,最后将所有的关联度和数值
相比较,就可以得到其他输入向量与向量
的相似程度,越接近
,那么就和
越相似。
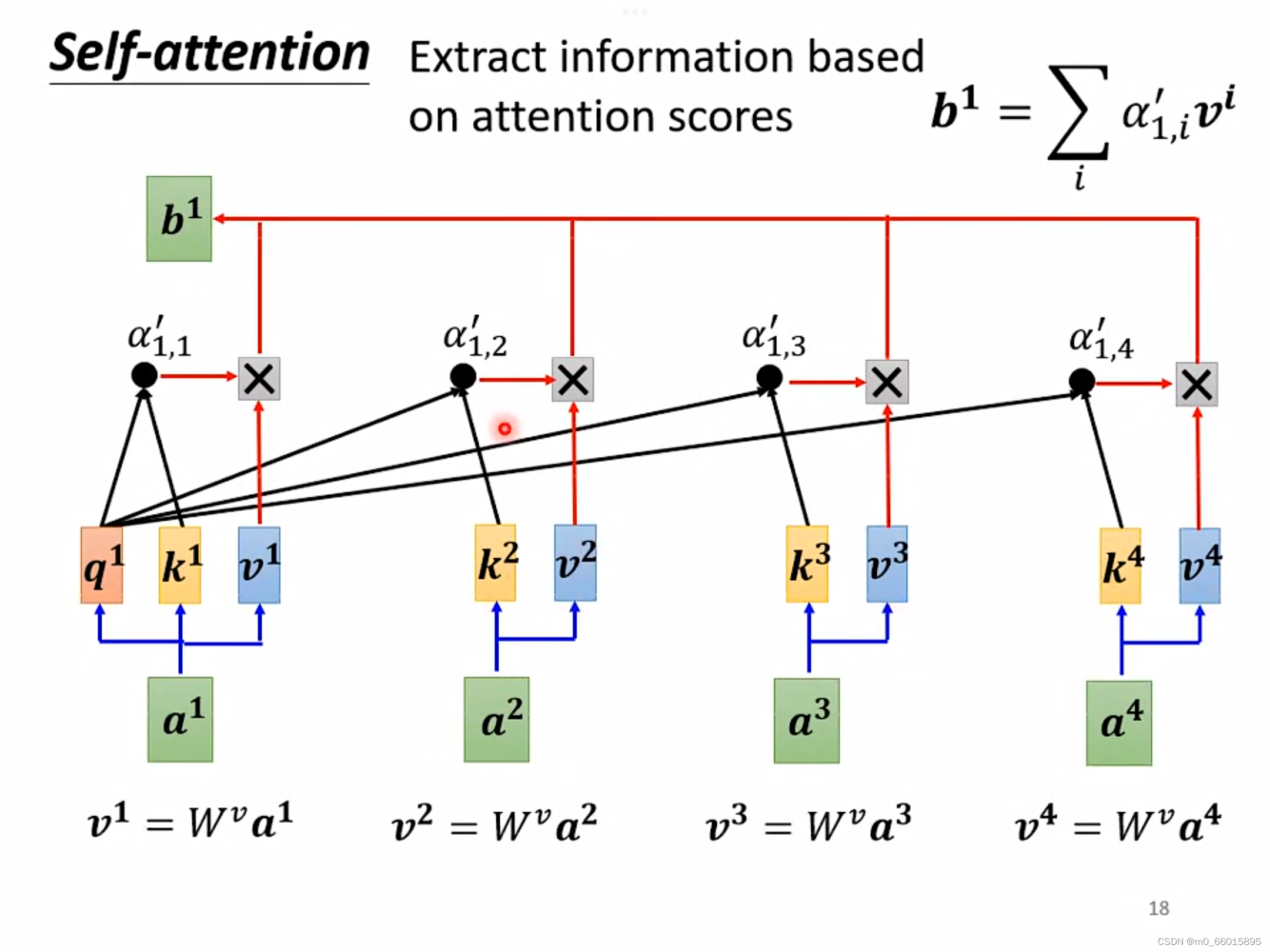
、
、
、
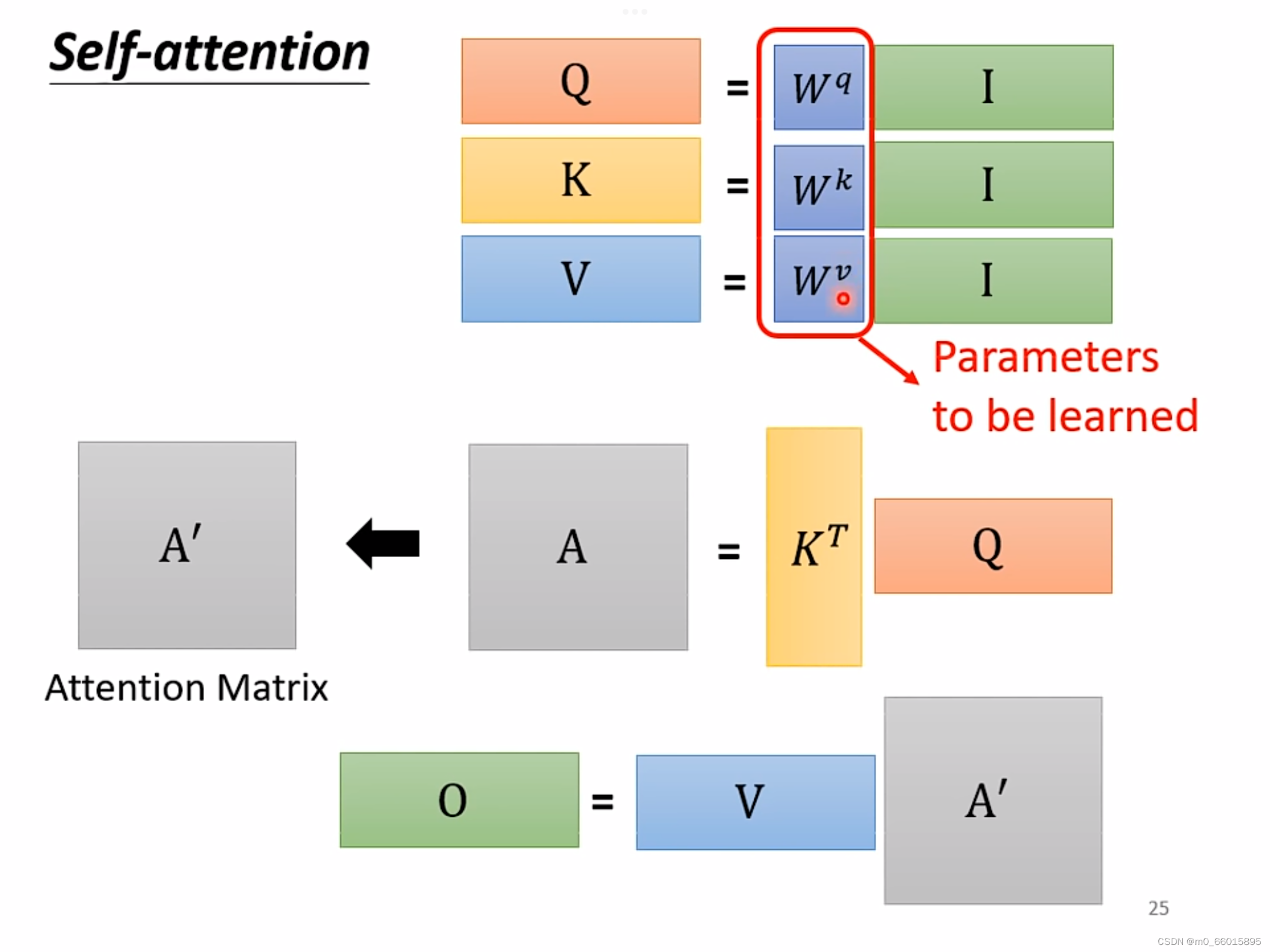
并不是依次产生而是同时被计算出来的
计算过程如下:

2. Muti-Head Self-attention
在transformation中,应用最广的一种self-attention机制叫做muti-head self-attention,这种attention相对之前的在attention而言,它对于每一个向量a可以具备多组的q,k,v来描述这一个向量,而之前的只用到了一组,使用多组q,k,v,那么就需要对每一组计算其b的值,有几组就有几个b值。不同的任务需要用到的head数目是不一样的,对于有些任务比如语音辨识,使用的head越多效果越好。
Q:为什么head越多越好呢?
A:在做self-attention的时候,就是用
去找相关的k,但是相关这件事情有不同的形式、不同的定义,因此需要更多的q负责不同种类的相关性。
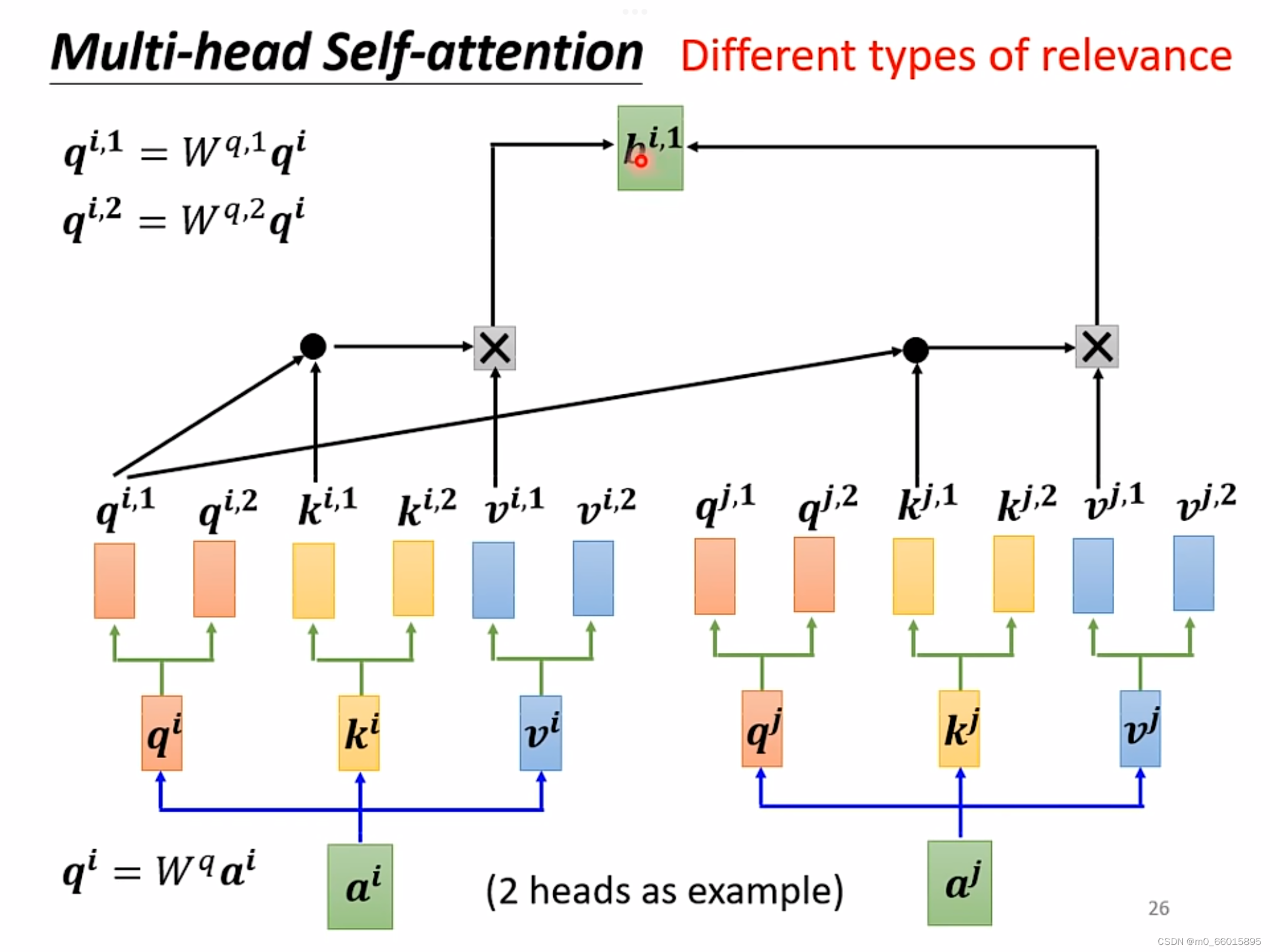
?以2个head为例计算:

3. Self-attention v.s. CNN
CNN可以看作简化版的Self-attention,因为在做CNN的时候只考虑receptive field里面的信息,而Self-attention是考虑全部的信息。(Self-attention如果设定一定的参数就可以做和CNN一样的事情)?
?Self-attention考虑的范围更大,它的模型自由度高,因此需要更多的data,data不够就有可能overfitting,而对于CNN这种有限制的模型,在data比较少的时候也不会容易overfitting。从下图的一个测试中可以看出,在资料量少的时候,CNN表现得比Self-attention好,而当资料量越老越多达到一定数量后,Self-attention反而会超过CNN。
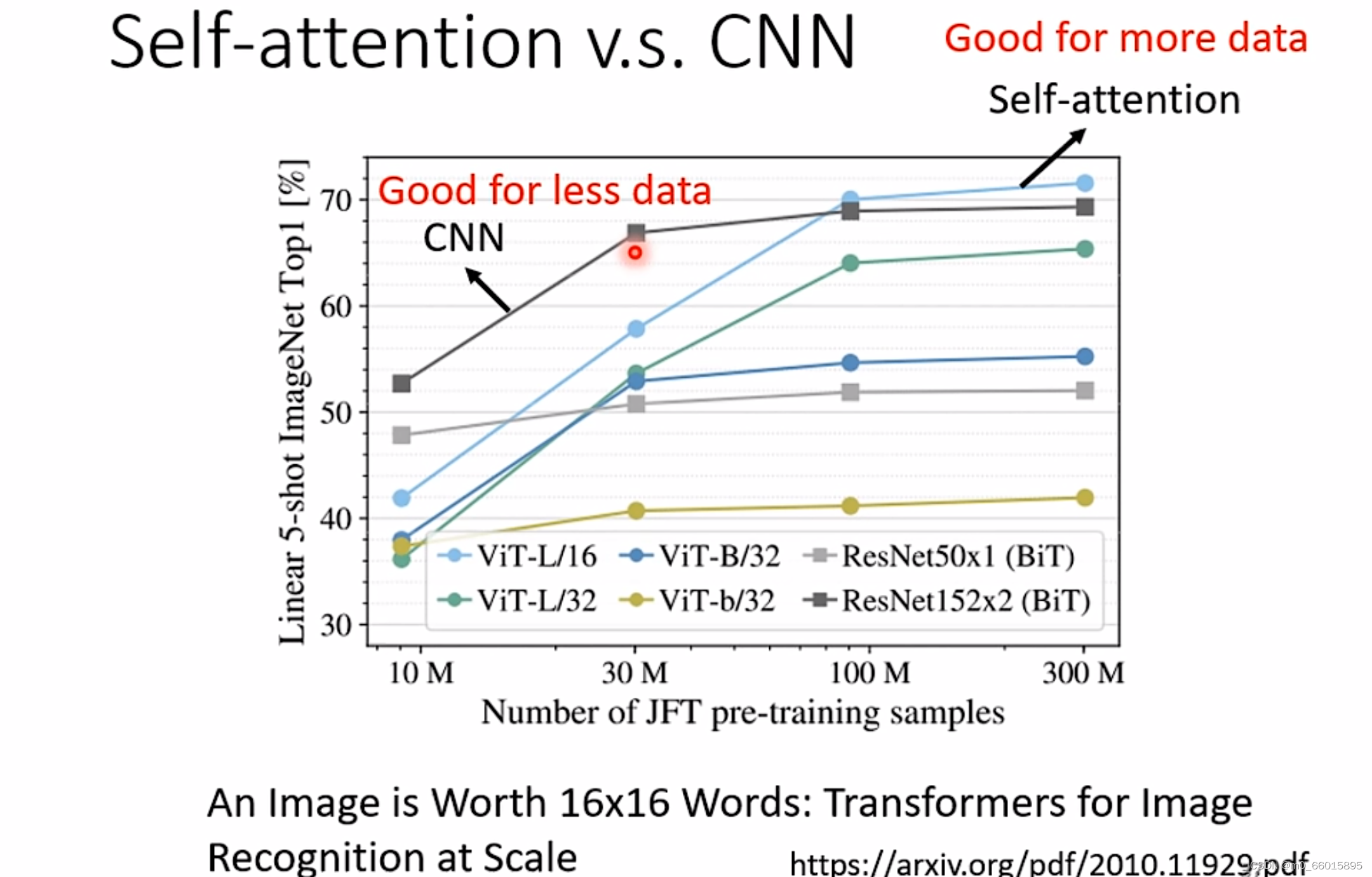
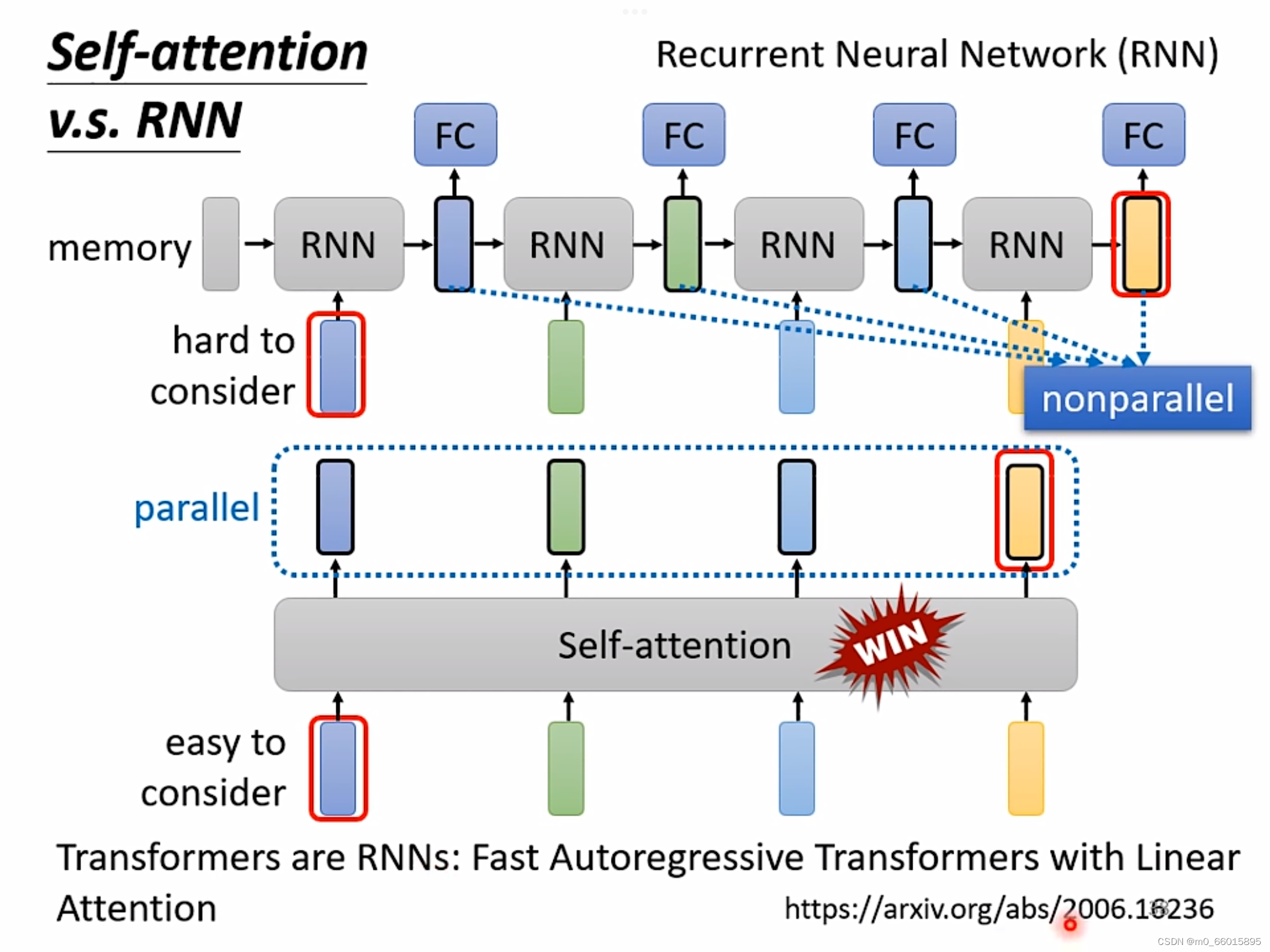
4. Self-attention v.s. RNN
共同点:都要处理一个input是一个sequence的状况
区别:①self-attention考虑了所有输入的向量,而RNN只能考虑左边已经输入的向量而不能考虑右边没有输入的向量。
②self-attention可以进行平行运算所有输出,而RNN不可以进行平行运算。
实现Self-attention
import math
import torch
import torch.nn as nn
class Self_attention(nn.Module):
def __init__(self, dim, dk, dv): # dim表示输入数据数据的特征数(维度),dk表示Q和K向量的维度,dv表示V向量的维度
super(Self_attention, self).__init__()
self.scale = dk ** -0.5 # scale表示根号dk分之一
self.query = nn.Linear(dim, dk) # 定义输出张量Q的线性层,输入数据的特征个数(维度)为dim,输出数据的特征个数(维度)为dk
self.key = nn.Linear(dim, dk) # 定义输出张量K的线性层,输入数据的特征个数(维度)为dim,输出数据的特征个数(维度)为dk
self.value = nn.Linear(dim, dv) # 定义输出张量V的线性层,输入数据的特征个数(维度)为dim,输出数据的特征个数(维度)为dv
def forward(self, x):
Q = self.query(x) # 根据输入的数据x,通过线性层得到张量Q,K,V
K = self.key(x)
V = self.value(x)
print("矩阵Q:", Q)
print(Q.shape) # Q的维度是(batch_size, num_queries, dim)
print("矩阵K:", K)
print(K.shape) # K的维度是(batch_size, num_keys, dim)
print("矩阵V:", V)
print(V.shape) # V的维度是(batch_size, num_values, dim)
# k.transpose(-2, -1),表示将k矩阵的最后两个维度交换
# 即将张量k的形状从(batch_size, num_keys, dim)转换为(batch_size, dim, num_keys),这样可以适应矩阵乘法的要求
attention = (Q @ K.transpose(-2, -1)) * self.scale
print("矩阵attention:", attention)
print(attention.shape)
# 对attention的最后一个维度做softmax
attention = attention.softmax(dim = -1)
# 将attention和V做点乘得到最终的输出x
x = attention @ V
return x
class PositionalEncoding(nn.Module):
def __init__(self, d_model, max_len): # d_model表示特征维度,max_len表示输入数据的个数
super(PositionalEncoding, self).__init__()
self.d_model = d_model
self.max_len = max_len
# 创建一个位置编码矩阵
pe = torch.zeros(max_len, d_model) # 初始化pe矩阵
position = torch.arange(0, max_len, dtype=torch.float) # 创建一个一维张量,元素按照0到max_len-1排列
print("position:", position)
# 在原位置1的维度上添加一个新的维度,相当于将一维的position中的每个元素独立放到一个维度中
# position的维度从(max_len,)变为了(max_len, 1)
position = position.unsqueeze(1)
print("position:", position)
# div_term = 1/10000^(2i/d_model) = exp(2i*(-log(10000)/d_model))
div_term = torch.exp(torch.arange(0, d_model, 2).float() * -(math.log(10000.0) / d_model))
# 将pe切片赋值,[:, ...]冒号表示选择所有的行,[:, 0::2]0表示从第0行开始以步长为2进行列的选择
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
# 在第0个维度上添加一个维度,将原来的(max_len, d_model)形状变为(1, max_len, d_model)
# 这个操作使得pe张量看起来就像是一个包含一个样本的批次,即批次大小为1
# 当需要在模型中使用一些不需要优化的张量或常数值,比如位置编码、标准化参数等时,这些张量可以通过 register_buffer 方法注册为模型的缓冲区,以便在模型的训练、保存和加载过程中进行管理
# 具体地说,self.register_buffer('pe', pe) 将 pe 张量注册为名为 'pe' 的模型缓冲区
# 这意味着 pe 张量将与模型一起保存和加载,但不会被视为模型的可训练参数
# 在模型的前向传播中,可以通过 self.pe 来访问这个缓冲区中的内容
pe = pe.unsqueeze(0)
self.register_buffer('pe', pe)
def forward(self, x):
# 通过位置编码给x添加位置信息
# self.pe[:, :x.size(1)] 是用于选择位置编码矩阵中相应位置的操作
# 具体来说,[:, :x.size(1)] 表示选择 self.pe 张量的第一个维度(批次维度)的所有元素,以及第二个维度(位置维度)中的前x.size(1)个元素
# 这个操作的目的是选择与输入张量x中序列长度相对应的位置编码
x = x + self.pe[:, :x.size(1)]
return x
SA_1 = Self_attention(dim=2, dk=2, dv=2)
PE_1 = PositionalEncoding(d_model=2, max_len=4)
x = torch.rand((1, 4, 2))
print("输入数据:",x)
x = PE_1(x)
print("编码后的输入数据:", x)
out = SA_1(x)
print("输入数据:",out)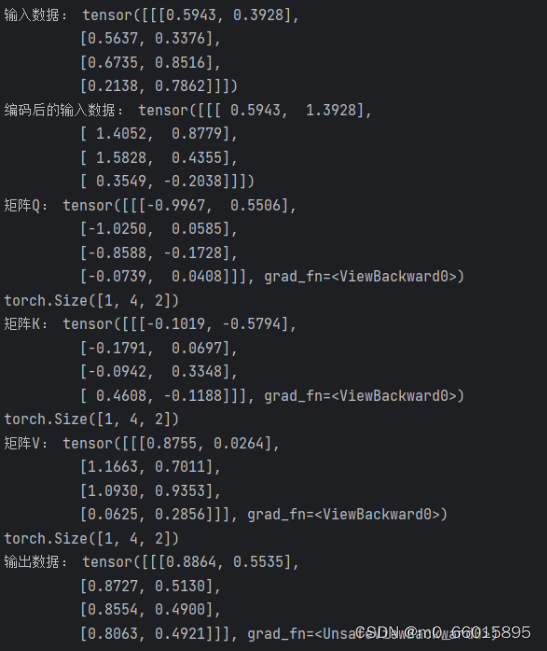
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Kubernetes 开发环境使用 Helm Charts 快速安装开源软件
- 基于SpringBoot的员工健康管理系统
- HTTP 常见协议:选择正确的协议,提升用户体验(下)
- 配置SSH+Sourcetree+Git
- 初阶:第一部分Python数据类型的知识框架思维导图
- 分享5个AI绘画关键词网站 让你的AI绘画创作更随心
- Flutter--常用技术文档
- 白马股选股策略
- Python学习之路-编码风格
- 《EDA技术实用教程(第六版)》学习笔记——第二章